Тесты как средство промежуточного и итогового контроля знаний по дисциплине "Информатика" в военном вузе
Автор: Савельева Светлана Владимировна, Валеева Ирина Харисовна
Журнал: Инновационное развитие профессионального образования @journal-chirpo
Рубрика: Образовательные технологии: наука и практика
Статья в выпуске: 2 (30), 2021 года.
Бесплатный доступ
Статья посвящена применению тестового контроля качества усвоения знаний в процессе изучения дисциплины «Информатика». Так как дисциплина «Информатика» является практико-ориентированной, то при составлении тестов необходимо использовать такие задания, которые охватывают не только определения и понятия, но и их практическое применение. В статье приведены формы тестовых заданий и представлены их практическая реализация и применение. Раскрываются проблемы анализа тестовых заданий в аспекте их сложности и количественного соотношения открытой, закрытой и полуоткрытой формы. Приводятся расчет коэффициента трудности каждого тестового задания и теста в целом для промежуточного контроля знаний, проверка теста на надежность методом расщепления по формулам Рюлона и Кьюдера - Ричардсона, определение валидности отдельных тестовых заданий с помощью расчета значений точечного бисериального коэффициента корреляции.
Тестирование, контроль знаний, усвоение, тестовые задания, форма тестовых заданий, закрытая форма, открытая форма, полуоткрытая форма, коэффициент сложности тестовых вопросов, надежность теста
Короткий адрес: https://sciup.org/142228717
IDR: 142228717 | УДК: 372.016:004
Текст научной статьи Тесты как средство промежуточного и итогового контроля знаний по дисциплине "Информатика" в военном вузе
Прослеживая процесс обучения, можно отметить, что он начинается с промежуточного контроля, сопровождается текущим и заканчи- вается контролем учебных достижений. Существуют разные способы проведения контроля и оценки знаний. По мнению Н. О. Прокофьевой, можно выделить пять этапов в эволюции развития контроля знаний, отражающих формы организации контроля знаний и роль преподавателя в этом процессе: традиционный, с использованием бумажных (не компьютерных) средств, с использованием технических устройств, компьютерный и удаленный. Как можно заметить, уже на втором этапе эволюции контроля знаний с использованием бумажных (не компьютерных) средств «используются заранее подготовленные бланки, содержащие контрольные задания (тесты)» [1, с. 434]. Следовательно, такой метод контроля, как тестирование, может применяться для текущей, промежуточной и итоговой проверки знаний.
Тестирование как форма контроля широко распространено в системе образования европейских стран и в России. В нашей стране примером может являться внедрение ЕГЭ как итогового тестирования школьников и его аналога промежуточного значения — ГИА, а также федерального интернет-экзамена и тестирования по другим технологиям в вузах.
Л. И. Жаркова, Н. В. Картушина определяют понятие «тест» как систему заданий, выполнение которых позволяет проверить уровень владения тем или иным предметом с помощью специально разработанной системы оценки приобретенных знаний [2]. По мнению Е. В. Шевчук, «тест — это инструмент, состоящий из ква-лиметрически выверенной системы тестовых заданий, стандартизированной процедуры проведения и заранее спроектированной обработки и анализа результатов, предназначенный для измерения качеств и свойств личности, изменение которых возможно в процессе систематического обучения» [3]. В новом словаре методических терминов и понятий «тест» определяется как задание стандартной формы, выполнение которого позволяет установить уровень и наличие определенных умений, навыков, способностей, умственного развития и других характеристик личности с помощью специальной шкалы результатов. Учебные тесты используются для проверки знаний, навыков, умений по изучаемой дисциплине [4, с. 309]. Таким образом, тестирование — это метод такой проверки знаний, умений и навыков, где испытуемый выполняет ряд специальных заданий, которые называют тестовыми [2].
По мнению В. С. Аванесова, педагогический тест определяется как система заданий возрастающей трудности, специфической формы, позволяющая качественно и эффективно измерить уровень и оценить структуру подготовленности обучающихся [5; 6]. Здесь термин «специфическая форма» объясняется тем, что задания теста не являются вопросами или задачами, это именно задания, выраженные в форме истинных или ложных суждений, зависящих от ответов.
По сравнению с другими формами контроля знаний тестирование обладает рядом достоинств, таких как: качество и объективность , которые достигаются за счет стандартизации процесса проведения теста, обработки и анализа результата; справедливость , так как все обучающиеся находятся в равных условиях, что исключает субъективизм; объемность — она состоит в возможности включать задания по всем темам дисциплины, определять уровень знаний как по предмету в целом, так и по отдельным его темам; точность , которая достигается с помощью шкалы оценивания (например, в шкале теста столько делений, сколько вопросов в тесте; в обычной шкале четыре деления: 2, 3, 4, 5); эффективность , заключающаяся во временных затратах: так, на тестирование целой группы затрачивается 30–40 минут, в зависимости от количества вопросов, на устный или письменный экзамен — не менее четырех часов; психологически комфортный инструмент контроля , так как все учащиеся поставлены в равные условия.
Существуют недостатки тестирования, которые также необходимо перечислить, чтобы понять, какие тестовые задания следует разработать для контроля учебной информации по дисциплине «Информатика». К отрицательным сторонам тестирования можно отнести следующие положения:
-
1) разработка квалитативного теста — трудоемкий процесс, направленный на составление тестовых вопросов и критериев оценки;
-
2) результаты тестирования не раскрывают причины некачественного усвоения знаний;
-
3) результаты тестирования не дают возможности проверить и оценить знания, связанные с их применением в творчестве;
-
4) объективность и справедливость теста требует обеспечения конфиденциальности (неразглашения) тестовых заданий, что трудно обеспечить;
-
5) случайное отгадывание ответа искажает результаты тестирования, приводит к необходимости учета вероятностной составляющей.
Исходя из перечисленных недостатков, отметим, что трудность разработки надежного теста требует особой углубленной подготовки, так как некорректно сформулированные вопросы дают ошибочные результаты и искажают впечатление о знаниях студентов [7]. Таким образом, как отмечают Е. Г. Жаринова и Е. В. Черняева, тестовые задания должны отвечать нескольким критериям и быть: 1) краткими и технологичными; 2) сформулированными логично и однозначно; 3) с одинаковыми для всех обучающихся правилами оценки ответов и инструкцией к выполнению [8].
Последние этапы развития контроля знаний (с использованием технических устройств, компьютерный и удаленный) [1] позволяют расширить рамки использования тестового контроля знаний благодаря применению информационных и цифровых технологий.
Существует большое количество систем дистанционного обучения. Одной из таких систем является модульная объектно-ориентированная динамическая обучающая среда (Moodle), известная как система управления обучением, или виртуальная обучающая среда. Она представляет собой свободное веб-приложение, распространяющееся по открытому лицензионному соглашению, и дает возможность создавать сайты для онлайн-обучения. В Moodle доступ- ны различные возможности для контроля успеваемости обучающихся, а также существует поддержка массовой регистрации с безопасной аутентификацией. Модуль Тест — один из сложных элементов системы Moodle — включает различные типы вопросов.
В педагогической литературе, связанной с разработкой тестовых заданий и тестов, как правило, выделяют задания закрытой, полуоткрытой и открытой формы. Закрытая форма предполагает отбор из готовых ответов путем выбора правильного варианта. К разновидностям закрытой формы тестовых заданий можно отнести задания для множественного выбора одного и нескольких правильных ответов. В Moodle существует возможность реализации таких тестовых заданий [9]. Ответы на вопросы с выбором одного правильного ответа можно составить так, чтобы была возможность отработать на каждом вопросе сразу три или более понятий (табл. 1). Выбирая правильный ответ, обучающийся невольно соотносит каждое определение с понятием, усваивая и запоминая три определения.
Таблица 1
Тестовые задания с выбором одного правильного ответа
|
Формулировка вопроса |
Формулировки ответов |
|
Дать определение понятия «идентификация» |
Идентификация — это процедура…
|
|
Дать определение понятия «аутентификация» |
Аутентификация — это процедура…
|
|
Дать определение понятия «авторизация» |
Авторизация — это процедура…
|
|
Такого же эффекта можно добиться, если ис- |
счисления, можно составить задание, включаю- |
|
пользовать тестовые задания с выбором нескольких правильных ответов. Так, изучая системы |
щее правильные ответы по основным системам счисления (табл. 2). |
Таблица 2
Тестовые задания с выбором нескольких правильных ответов
|
Формулировка вопроса |
Формулировки ответов |
|
Дана шестнадцатеричная система счисления . Выберите число, являющееся основанием системы счисления, и ряд чисел, являющихся базисными для данной системы счисления |
2; 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, е, f 8; 0, 1, 2, 3, 4, 5, 6, 7 10; 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 16 ; 0, 1 |
Окончание таблицы 2
|
Формулировка вопроса |
Формулировки ответов |
|
|
Дана восьмеричная система счисления . |
2; |
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, е, f |
|
Выберите число, являющееся основанием |
8 ; |
0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
|
системы счисления, и ряд чисел, являющихся |
10; |
0, 1, 2, 3, 4, 5, 6, 7 |
|
базисными для данной системы счисления |
16; |
0, 1 |
|
Дана двоичная система счисления . Вы- |
2 ; |
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, е, f |
|
берите число, являющееся основанием |
8; |
0, 1, 2, 3, 4, 5, 6, 7 |
|
системы счисления, и ряд чисел, являющихся |
10; |
0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
|
базисными для данной системы счисления |
16; |
0, 1 |
|
Дана десятичная система счисления . Вы- |
2; |
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, е, f |
|
берите число, являющееся основанием |
8; |
0, 1, 2, 3, 4, 5, 6, 7 |
|
системы счисления, и ряд чисел, являющихся |
10 ; |
0, 1 |
|
базисными для данной системы счисления |
16; |
0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
Полуоткрытая форма включает задания для подбора готовых ответов в пары или последовательный ряд [9]. В первом случае каждому из заданных элементов одной части подбирается один соответствующий элемент из другой части, во втором случае в задании предлагается определить, в какой последовательности должны находиться представленные ответы (табл. 3, 4).
Таблица 3
Тестовые задания подбора готовых ответов в пары или последовательный ряд
|
Формулировка вопроса и ответа |
|
|
Число 132 дано в разных системах счисления. Осуществить упорядочивание данных чисел по возрастанию в десятичной системе счисления. 132 16 , 132 7 , 132 10 , 132 9 , 132 8 |
|
|
Используя перетаскивание элементов, установите соответствие между системой счисления, основанием и базисными числами. |
|
|
двоичная СС |
8; 0, 1, 2, 3, 4, 5, 6, 7 |
|
десятичная СС |
16; 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, е, f |
|
восьмеричная СС |
2; 0, 1 |
|
шестнадцатеричная СС |
10; 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
|
4; 0, 1, 2, 3 |
|
|
7; 0, 1, 2, 3, 4, 5, 6 |
|
|
На представленном рисунке приведены характеристики систем счисления, установите соответствие, перетащив её название на изображение. Основание - 2; Основание - 16, базисные числа - 0,1; базисные числа - 0, 1,2,3, 4,5,6. 7,8,9, a, b, с, d,e,f, Двоичная СС Шестнадцатеричная СС Основание - 10, Основание - 8, базисные числа - 0, 1,2,3,4,5,6, 7,8,9; базисные числа - 0, 1,2,3.4, 5, 6, 7; Десятичная СС Восьмеричная СС |
|
Задания открытой формы — это задания для нения которого респондент записывает ответ сло-краткого свободного ответа, в результате выпол- вом, словосочетанием или числом [9] (табл. 4).
Таблица 4
Тестовые задания с кратким свободным ответом
Формулировка вопроса
Вставьте пропущенные числа. Для восьмеричной системы счисления: основание — _____, базисные числа — __________________________________
Вставьте пропущенные слова и адреса ячеек. Адрес ячейки, не изменяющийся в процессе копирования или перемещения формулы, называется ______________. Адрес ячейки, изменяющийся в процессе копирования или перемещения формулы, называется ______________.
Даны два адреса А1, $D$8. Относительный адрес _________. Абсолютный адрес__________
Рассмотрев реализацию тестовых заданий в Moodle , мы пришли к выводу, что можно решить проблему объективности и справедливости тестов, обеспечить конфиденциальность тестовых заданий, если использовать в процессе разработки тестовых заданий перемешивание ответов к заданиям. В данном случае обучающиеся не могут подсказать номер правильного ответа.
При создании тестов необходимо решить вопрос о соотношении количества тестовых заданий открытой, закрытой и полуоткрытой формы. Так, например, в тесте из 20 заданий рекомендуется использовать не более 3 (17 %) тестовых заданий открытой формы, приблизительно 7 (33 %) заданий полуоткрытой формы (4 — для составления пар соответствия, 3 — на последовательность рядов), оставшиеся 10 (50 %) заданий предлагается давать в закрытой форме (по 5 заданий с выбором одного и нескольких правильных ответов).
Надежность — одна из характеристик теста, которая показывает точность измерений, а также их устойчивость в отношении воздействий случайных факторов. Существует два вида надежности: характеристика устойчивости и характеристика внутренней согласованности.
Как правило, надежность предпочитают рассматривать как внутреннюю согласованность, поскольку в этом случае не требуется повторного тестирования обучающихся. Интерпретация полученного значения такова: если найденный показатель находится в пределах от 0,9 до 1, то тест имеет очень высокую степень надежности; если от 0,8 до 0,9, то тест обладает хорошей надежностью; если от 0,7 до 0,8, то надежность теста считается удовлетворительной; если менее 0,7, то надежность теста низкая.
Воспользуемся формулой Рюлона [10] для расчета коэффициента корреляции теста, состоящего из 30 вопросов, проводимого в группе из 15 учащихся. Для удобства обработки результатов тестирования необходимо составить матрицу результатов выполнения теста обучающимися, где 1 — правильный ответ на задание, 0 — неправильный ответ или пропуск задания. Промежуточные расчеты коэффициента корреляции приведены в таблице (рис. 1). Исходя из данных, получаем значение r ≈ 0,896, которое указывает на хорошую надежность теста. Обработка результатов осуществлялась с помощью приложения MS Excel .
|
Номер учащегося i |
Баллы по нечетным заданиям /, |
Баллы по четным заданиям Xi |
X.—Y. |
/ 1А \ 1 (й-Ю--^-^ 1 |
|
1 |
10 |
10 |
0 |
0,04 |
|
2 |
14 |
13 |
0 |
0,04 |
|
3 |
э |
11 |
2 |
3,24 |
|
4 |
13 |
11 |
-3 |
10,24 |
|
5 |
8 |
7 |
-1 |
1,44 |
|
6 |
12 |
11 |
0 |
0,04 |
|
7 |
11 |
11 |
0 |
0,04 |
|
8 |
12 |
10 |
-2 |
4,84 |
|
9 |
13 |
13 |
-1 |
1,44 |
|
10 |
12 |
13 |
1 |
0,64 |
|
8 |
э |
1 |
0,64 |
|
|
12 |
12 |
13 |
2 |
3,24 |
|
13 |
5 |
6 |
2 |
3,24 |
|
14 |
6 |
3 |
2 |
3,24 |
|
15 |
10 |
10 |
0 |
0,04 |
|
Сумма |
155 |
156 |
3 |
32,4 |
|
Среднее " арифметическое |
10,33 |
10,4 |
0,2 |
2,31 |
Рис. 1. Подсчет надежности методом расщепления
Как правило, проверка надежности теста проводится разными методами. Часто в качестве еще одного численного показателя надежности теста применяют формулу Кьюдера — Ричардсона [11]. Используя в качестве исходных данных ранее ука- занную матрицу результатов выполнения теста, проведя промежуточные вычисления (рис. 2), получаем результат r ≈ 0,901, что подтверждает расчеты, выполненные предыдущим методом. Интерпретация полученного значения аналогична.
|
Номер учащегося i |
Кол-во неправильных ответов |
Кол-во правильных ответов |
РГ<1 |
Отклонение баллов учеников от среднего значения |
Квадрат отклонения |
|
1 |
10 |
20 |
0,22 |
-0,73 |
0,54 |
|
2 |
3 |
0,09 |
6,27 |
39,27 |
|
|
3 |
10 |
20 |
0,22 |
-0,73 |
0,54 |
|
4 |
6 |
24 |
0,16 |
3,27 |
10,67 |
|
5 |
15 |
15 |
0,25 |
-5,73 |
32,87 |
|
6 |
7 |
23 |
0,18 |
2,27 |
5,14 |
|
7 |
8 |
22 |
0,20 |
1,27 |
1,60 |
|
8 |
8 |
22 |
0,20 |
1,27 |
1,60 |
|
э |
4 |
26 |
0,12 |
5,27 |
27,74 |
|
10 |
5 |
25 |
0,14 |
4,27 |
18,20 |
|
11 |
13 |
17 |
0,25 |
-3,73 |
13,94 |
|
12 |
5 |
25 |
0,14 |
4,27 |
18,20 |
|
13 |
19 |
11 |
0,23 |
-9,73 |
94,74 |
|
14 |
16 |
14 |
0,25 |
-6,73 |
45,34 |
|
15 |
10 |
20 |
0,22 |
-0,73 |
0,54 |
|
Сумма |
139 |
311 |
2,86 |
0,00 |
310,93 |
|
Среднее арифметическое |
9,27 |
20,73 |
Рис. 2. Расчет надежности с помощью формулы Кьюдера — Ричардсона
На начальном этапе апробации теста значение коэффициента может быть значительно меньше 0,7, что свидетельствует о низкой его надежности. В этом случае полученный результат следует расценивать так: в разрабатываемой методике присутствуют задания, снижающие значение данного коэффициента в силу своей специфичности. Выявить их можно путем определения валидности отдельных заданий теста с помощью подсчета значений точечного бисе-риального коэффициента корреляции (rpbis)j [11]. Оценка валидности задания теста позволяет делать выводы о том, насколько оно соответствует цели создания теста. Задание считается валидным, если значение (rpbis)j ≥ 0,5.
Применение формулы нахождения значений точечного бисериального коэффициента корреляции для данных по заданию № 5 рассматриваемого примера матрицы дает высокое значение (рис. 3). Так как 5-й, 11-й, 13-й и 14-й обучающиеся выполнили данное задание неверно, то
I № 15+17 + 11 + 14 = 57 =1425.
■ ■ 4 4
Остальные обучающиеся дали правильный ответ на это задание, поэтому
ГО -
20 + 27 + 20 + 24+23 + 22 + 22+26 + 25+25+20 п
И
= 23,09.
Стандартное отклонение, подсчитанное для рассматриваемого примера ранее, составляет Sx = 4,71. Тогда
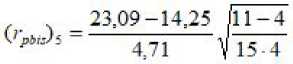
« 0,86.
Анализ значений полученных коэффициентов указанного фрагмента таблицы указывает на одно неудачное задание — № 7, которое имеет низкую валидность и должно быть удалено из теста.
Сложность заданий должна соответствовать уровню подготовки обучающихся, поэтому для каждого тестового задания необходимо опреде- лить коэффициент трудности. Для его расчета используют формулу:
где pj — доля правильных ответов на j-е задание, Rj — количество обучающихся, правильно выполнивших j -е задание, n — количество тестируемых обучающихся.
Произведя расчеты показателя трудности тестовых заданий для ранее указанной матрицы и выразив полученные значения в процентах (рис. 4), получим долю правильных ответов на первое задание — 80 %. Это значение скорее отражает легкость задания: его выполнили 80 % обучающихся тестируемой группы. Оценивая остальные результаты, видим, что задания 3, 6, 9, 10, 11 вызвали у некоторых обучающихся затруднения в процессе их выполнения. Вычислив показатель трудности для теста в целом, получим значение 69 %, что свидетельствует о средней степени его сложности. Проведенные теоретические и практические исследования показали, что тесты могут быть использованы как средство промежуточного и итогового контроля знаний по дисциплине «Информатика» в военном вузе.
|
номер учащегося i |
Номе |
р задания |
|||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
Индивидуальный балл учащегося |
||
|
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
20 |
|
|
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
27 |
||||
|
3 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
20 |
|||
|
4 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
24 |
|||
|
5 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
15 |
||||
|
6 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
23 |
|
|
7 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
22 |
|
|
8 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
22 |
|||||
|
9 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
26 |
|
|
10 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
25 |
|
|
и |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
17 |
|
|
12 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
25 |
||
|
13 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
11 |
|
|
14 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
14 |
||
|
15 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
20 |
|
|
Кол-во правильных ответов |
12 |
13 |
10 |
11 |
11 |
10 |
11 |
14 |
10 |
10 |
8 |
||
|
Кол-во неправильных ответов |
3 |
2 |
5 |
4 |
4 |
5 |
4 |
1 |
5 |
5 |
7 |
||
|
17,00 |
14.00 |
16,40 |
17,25 |
14,25 |
17,00 |
18,75 |
14,00 |
18,20 |
17,40 |
19,00 |
|||
|
21,67 |
21,77 |
22,90 |
22,00 |
23,09 |
22,60 |
21,45 |
21,21 |
22,00 |
22,40 |
22,25 |
|||
|
Валидность |
0,41 |
0,58 |
0,67 |
0,46 |
0,86 |
0,58 |
0,26 |
0,40 |
0.39 |
0,52 |
0,36 |
||
Рис. 3. Расчет значений коэффициента бисериальной корреляции
|
Номер учащегося i |
Номер задания |
Индивидуальный балл учащегося |
|||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|||
|
1 |
1 |
1 |
1 |
с |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
20 |
|
|
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
27 |
||
|
3 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
20 |
||
|
4 |
1 |
с |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
24 |
|||
|
5 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
15 |
||
|
6 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
23 |
|
|
7 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
22 |
||
|
8 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
22 |
|
|
9 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
26 |
|
|
10 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
25 |
||
|
11 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
17 |
|
|
12 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
25 |
|
|
13 |
1 |
0 |
0 |
с |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
11 |
|
|
14 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
14 |
||
|
15 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
20 |
|
|
Кол-во правильных ответов |
12 |
13 |
10 |
11 |
11 |
10 |
и |
14 |
10 |
10 |
8 |
||
|
Трудность |
80% |
87% |
67% |
73% |
73% |
67% |
73% |
93% |
67% |
67% |
53% |
||
Рис. 4. Значения трудности заданий теста
Список литературы Тесты как средство промежуточного и итогового контроля знаний по дисциплине "Информатика" в военном вузе
- Прокофьева, Н. О. Вопросы организации компьютерного контроля знаний / Н. О. Прокофьева // Образовательные технологии и общество. — 2006. — № 9 (1). — С. 433-440. — URL: https://cyberleninka.rU/article/n/voprosy-organizatsii-kompyuternogo-kontrolya-znaniy/viewer (дата обращения: 13.04.2021).
- 2.Жаркова, Л. И. Тестирование как метод контроля знаний при обучении иностранным языкам / Л. И. Жаркова, Н. В. Картушина // Мир науки. — 2017. — Т. 5. — № 2. — URL: http:// mir-nauki.com/PDF/14PDMN217.pdf (дата обращения: 13.04.2021).
- Шевчук, Е. В. Современные технологии в педагогическом образовании / Е. В. Шевчук, Н. С. Кольева. — Алматы : Отан, 2016. — 130 с.
- Азимов, Э. Г. Новый словарь методических терминов и понятий (теория и практика обучения языкам) / Э. Г. Азимов, А. Н. Щукин. — Москва : Изд-во «ИКАР», 2009. — 448 с. — ISBN 978-5-7974-0207-7.
- Аванесов, В. С. Тесты, теория и методика их разработки / В. С. Аванесов // Управление школой. — 1999. — № 28 (124). — С. 8-14.
- Аванесов, В. С. Теория и методика педагогических измерений (Материалы публикаций в открытых источниках и Интернет) / В. С. Аванесов. — URL: http://www.charko.narod.ru/tekst/ biblio/Avanesov_Teoriya_i_metod_ped_izmer.pdf (дата обращения: 13.04.2021).
- Щапов, А. Тестовый контроль в системе рейтинга / А. Щапов, Н. Тихомирова, С. Ершиков, Т. Лобова // Высшее образование в России. — 1995. — № 3. — С. 100-102.
- Жаринова, Е. Г. Использование тестов и тестовых заданий на контрольных занятиях по английскому языку / Е. Г. Жаринова, Е. В. Черняева // Научно-практическая конференция в рамках «Недели науки» ФИЯ МАИ-НИУ, посвященная 55-летию полета Ю. Гагарина (г. Москва, 07 апреля 2016 г.). Сборник докладов. Выпуск № 8. — Москва : Перо, 2016. — С. 43-46.
- Савельева, С. В. Практические основы проектирования тестов обучения и контроля / С. В. Савельева. — 2-е изд. — Челябинск : ЧИРПО, 2017. — 120 с.
- Расчет и анализ характеристик теста (для повышения уровня педагогического измерения). — URL: http://tester.quali.me/help.php (дата обращения: 13.04.2021).
- Статистический анализ качества тестовых заданий и тестов. — URL: http://www.plam. ru/pedagog/kontrol_kachestva_obuchenija_pri_attestacii_kompetentnostnyi_podhod/p8.php (дата обращения: 13.04.2021).


