Учебно-исследовательская программная система LOCOPT для поддержки преподавания численных методов нелинейной оптимизации

При подготовке студентов бакалавриата естественнонаучных направлений подготовки нередко приходится сталкиваться с тем, что традиционные пути преподавания численных методов математического программирования, преимущественно основанные на изложении теории их построения и аналитическом исследовании свойств (условия сходимости, оценки скорости сходимости и т.п.) [1-3] являются недостаточными и приводят к трудностям освоения материала у части студентов. Особенно это относится к прикладным и инженерным направлениям подготовки, таким, например, как «Прикладная математика и информатика», «Фундаментальная информатика и информационные технологии» [4]. Для студентов этой категории кроме теоретического изучения материала важной составляющей обучения является возможность его активного экспериментального освоения. Эта возможность может быть реализована в весьма различных формах, но в любом случае предполагает использование программных систем, поддерживающих широкие возможности компьютерного эксперимента при избавлении студента от рутинных вычислений, а также автоматизирующих обработку и визуализацию результатов.

Выбор вида программной поддержки тесно связан с применяемой методикой преподавания. Рассмотрим несколько достаточно распространенных вариантов. Одним из часто используемых является проектный подход, который, как правило, предполагает самостоятельную реализацию студентом изучаемого метода с последующим его применением к решению предложенной учебной задачи. При этом для уменьшения затрат на программирование, обработку и визуализацию результатов наиболее естественным является использование программных сред в виде универсальных математических пакетов, таких как MATLAB, Maple, Mathematica, поскольку широкие возможности их библиотек позволяют не отвлекаться на поддержку многих рутинных операций. В качестве примера использования такого подхода (применительно к задачам моделирования) укажем [5].

Принципиально иная возможность — разработка и применение программного обеспечения в виде компьютерных тренажеров (см. описание в [6]), которые фактически принуждают студентов весьма хорошо освоить всю «технику» изучаемых численных алгоритмов, однако при этом не предоставляют, как правило, развитых средств для их экспериментального исследования. Согласно [6], применение компьютерных тренажеров заметно повышает успеваемость, что, вероятно, связано с закреплением преимущественно «знаниевой» составляющей приобретаемых компетенций.

Еще одна возможность (со своим уникальным обучающим потенциалом) состоит в разработке и использовании специализированных программ учебноисследовательского характера, обладающих весьма развитым, интуитивно понятным и разнообразным инструментарием, позволяющим в доступной и максимально наглядной графической форме проводить детальное исследование структур решаемых задач оптимизации, а также эксперименты на широком наборе численных методов с максимальными возможностями постоянного наблюдения за внутренними вычислительными процессами. Программное обеспечение такого типа можно назвать программными лабораториями, поскольку в них должны быть включены разнообразные инструменты для постановки задач, управления расчетами, наблюдения и исследования. Примерами таких систем в области численных методов математического программирования можно считать программную лабораторию для исследования методов одномерной глобальной оптимизации «АБСОЛЮТ» [7], а также программную лабораторию «LocOpt» по многомерной локальной оптимизации, включая общие методы учета ограничений (в [8] приведены математическое описание алгоритмического наполнения этой системы и примеры возможного построения программ лабораторного практикума с ее использованием).

В отличие от программных тренажеров [6] программные лаборатории являются компьютерными приложениями принципиально иного типа. В них не закладывается какой-либо конкретной последовательности действий по изучению материала, но зато предоставлены максимально гибкие возможности многовариантного изучения соответствующей предметной области (в случае LocOpt – численных методов конечномерной условной локальной оптимизации). Программные лаборатории допускают разнообразие методик их использования преподавателями (например, при организации лабораторных практикумов), а также самими студентами в целях самообучения (заметим, что его эффективность существенно зависит от уровня владения теорией изучаемых численных методов, поскольку требует от студента способности самостоятельно ставить перед собой вопросы для исследования с использованием программной лаборатории).

Кроме перечисленных типов программного обеспечения и связанных с ним методик обучения существуют и широко используются компьютерные разработки промежуточных типов. В качестве примера укажем на программный комплекс [9], используемый для построения математических моделей механических систем и исследования причин самовозбуждения колебаний. По структуре построения и возможностям он близок к программным лабораториям.

Таким образом, различные методики компьютерного обучения численным методам оптимизации требуют принципиально различного программного обеспечения, однако программные системы различных типов не исключают, а дополняют друг друга.

Концепция построения и обзор алгоритмического наполнения программной лаборатории LocOpt

Программная лаборатория LocOpt предназначена для исследования численных методов локальной оптимизации, включая общие методы учета ограничений. Исходный код программы написан на языке C++ для среды разработки C++Builder, автономный исполняемый файл является 32-разрядным приложением для операционных систем семейства Windows. Исследование методов выполняется на специально конструируемых или выбираемых пользователем из репозитория задачах оптимизации с ограничениями–неравенствами.

Каждая решаемая задача определяется размерностью N вектора переменных y (возможны значения N от 2 до 5), гиперинтервалом P, описывающим диапазоны изменения каждой из переменных y i , заданием выражения для минимизируемой функции f(y), набором функций ограничений–неравенств, значениями верхних и нижних ограничителей для этих функций, текущим положением начальной точки запуска локального метода. Можно использовать задачи без функций ограничений.

В программной системе LocOpt предусмотрен предопределенный набор функций и задач оптимизации, а также имеется специализированный многофункциональный конструктор функций и задач. Конструктор функций позволяет изменять, создавать и сохранять в специальном репозитории на диске новые наборы функций в виде строковых формульных выражений с набором переменных и закрепленными параметрами, а также указанными диапазонами изменения переменных. При работе с конструктором любая функция может быть визуализирована в отдельном плавающем окне в виде картины ее линий равного уровня. Конструктор задач позволяет редактировать встроенные задачи оптимизации, а также строить новые с использованием технологии Drag and Drop (см. рис. 1).

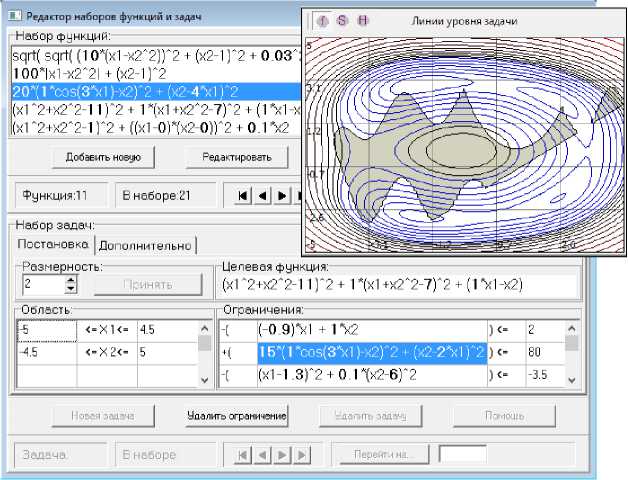
Рис. 1. Вид окна конструктора функций и задач в процессе синтеза новой задачи; поверх окна конструктора открыто плавающее окно графического отображения, допустимое множество выделено серым цветом

При создании новой задачи достаточно мышкой захватить из текущего открытого набора подходящие функции и перетащить их в специальные области конструктора задач, определяя тем самым минимизируемую функцию f(y), а также функции ограничений g i (y), (i = 1,…,m). Для функций ограничений также назначаются знаковые множители ±1 и значения верхних ограничителей. При просмотре и добавлении новых постановок задач оптимизации поддерживается опция их графического отображения в виде линий равного уровня минимизируемой функции (при N > 2 – в выбранном сечении), а также в виде границ и выделения цветом допустимого множества. Созданные наборы задач сохраняются на диске в специальном репозитории и могут быть открыты в следующих сеансах работы.

Для дальнейшего использования текущая задача должна быть направлена в окно эксперимента. Окно эксперимента является основным дочерним типом окна программной лаборатории LocOpt, имеющей формат MDI-приложения. Главное окно является окном рамки, внутри которого открываются дочерние окна экспериментов, а также управляющие диалоговые окна. Основные инструменты управления программной лабораторией находятся в верхней области главного окна и реализованы в виде главного меню приложения, а также двенадцати динамически перемещаемых панелей инструментов (см. рис. 2). Можно создать любое количество окон экспериментов с помещенными в них одинаковыми или разными задачами.

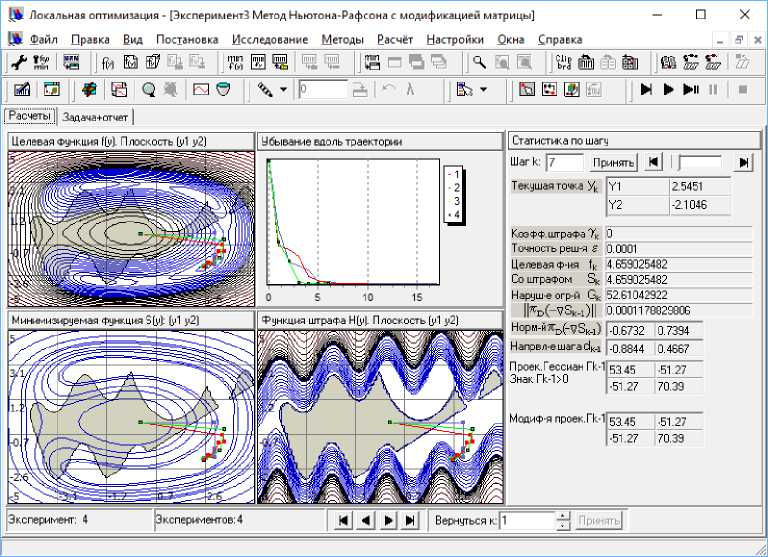
Рис. 2. Вид главного окна программной лаборатории LocOpt с развернутым в нем окном эксперимента, в окне приведены траектории поиска безусловного локального минимума тремя методами при отключенных ограничениях

В LocOpt принята следующая концепция учета ограничений–неравенств. Во-первых, ограничения можно отключить. Во-вторых, если ограничения не отключены, то можно использовать один из общих методов учета ограничений: метод внешнего степенного штрафа (ВСШ) или метод модифицированных функций Лагранжа (МФЛ). В обоих случаях исходная задача с функциональными ограничениями–неравенствами, определенная на заданном гиперинтервале P, заменяется семейством вспомогательных задач, также определенных на P, но уже без функциональных ограничений– неравенств. Минимизируемые функции этих вспомогательных задач определяются через значения всех функций исходной задачи, а также зависят от специальных параметров: коэффициента штрафа γ , а для метода МФЛ еще и от вектора λ оценок множителей Лагранжа. Обозначим эти вспомогательные минимизируемые функции через S γ (y) для метода ВСШ и через S γ (y, λ ) для метода МФЛ. Если в исходной задаче нет функциональных ограничений, то эти вспомогательные функции не зависят от параметров γ , λ и совпадают с минимизируемой функцией исходной задач и f(y). Таким образом в LocOpt методы безусловной локальной оптимизации всегда применяются именно к функциям вспомогательных задач на гиперинтервале P.

Заметим, что используемые алгоритмы учета ограничений (как метод штрафов [1], так и МФЛ [2]) предполагают решение серий вспомогательных задач с настройкой параметров γ и λ в процессе решения задачи для обеспечения сходимости . Применяемые алгоритмы автоматической настройки детально описаны в [3]. Однако, поскольку программная лаборатория ориентирована прежде всего на экспериментальное исследование численных методов, система поддерживает несколько различных режимов. В зависимости от их выбора можно отключить ограничения и решать задачу безусловной оптимизации в P, а можно ограничения включить, но отключить автоматическую настройку параметров и установить ручное изменение коэффициентов штрафа в методе ВСШ, а для метода МФЛ при отключении автоматической настройки можно установить либо ручное задание как множителей Лагранжа, так и коэффициента штрафа, либо выбрать автоматическую настройку множителей Лагранжа при фиксированном коэффициенте штрафа.

Заметим, что любое изменение параметров γ , λ приводит к обновлению графического отображения структуры вспомогательной функции в окне эксперимента. Наблюдение за этими изменениями позволяет с содержательной точки зрения правильно понять роль настройки параметров. Структура отображения информации в окне эксперимента на рис. 2 следующая. Блок графического отображения включает четыре позиции для отображения информации разных видов: вверху слева отображается вид исходной задачи, под ним – текущий вид вспомогательной задачи с S γ (y) или S γ (y, λ ), справа внизу – вид функции разности H(y) = S γ (y) – f(y) или H(y) = S γ (y, λ ) – f(y).

Используемые алгоритмы автоматической настройки γ (см. [3]) зависят от набора параметров, значения которых можно изменять с помощью специального диалогового окна, доступного либо через главное меню, либо панель инструментов.

Для решения вспомогательных задач, порождаемых общими методами учета ограничений ВСШ и МФЛ, могут применяться любые методы безусловной локальной оптимизации из поддерживаемого списка. В учебных целях в список включены представители методов нулевого, первого и второго порядков, причем как наиболее простые (и часто неэффективные), так и более сложные эффективные методы. Студенты должны сами оценить целесообразность использования каждого.

Методы нулевого порядка представлены двумя методами прямого поиска: Нелдера–Мида и Хука–Дживса. В качестве простых методов первого и второго порядков включены следующие: наискорейший градиентный поиск и метод Ньютона. Более сложные методы второго порядка: Ньютона–Рафсона (метод Ньютона с регулировкой шага с помощью одномерной минимизации), а также Ньютона–Рафсона с коррекцией матрицы Гессе на положительную определенность модифицированным преобразованием Холесского (см. описание в [3] и [8]). Эффективные методы первого порядка представлены четырьмя методами: квазиньютоновский (переменной метрики) DFP–метод, DFP–метод с коррекцией оценочной матрицы модифицированным преобразованием Холесского, метод сопряженных градиентов Флетчера–Ривса, а также эвристический метод Шора Н.З. растяжения пространства. Все методы первого и второго порядков (кроме метода Ньютона) используют алгоритм выбора шагового множителя на основе одномерной минимизации [3], [8]. Параметры этого алгоритма задаются в специальном диалоговом окне. В программной лаборатории полностью открыт доступ к общим параметрам методов и к их индивидуальным наборам параметров.

Заметим, что в LocOpt все решаемые задачи определяются на заданных в их постановках гиперинтервалах P. Поэтому хотя перечисленные выше численные методы были названы методами безусловной локальной оптимизации, в действительности это не совсем так. Все эти методы в LocOpt специальным образом модифицированы для возможности работы при ограниченных интервалах изменения по каждой переменной. Эти модификации подробно описаны в [3].

Основные инструменты исследования задач и численных методов

Инструменты исследования решаемых задач поясним вначале на примере двумерного случая. После выбора исследуемой задачи из репозитория или после её создания в окне конструктора задач она отправляется в окно эксперимента. По умолчанию она отображается в трёх из четырех позиций этого окна, как это было описано для на рис. 2 (позиция вида исходной формы задачи, позиция вида вспомогательной функции S, позиция вида аддитивной добавки H к минимизируемой функции f). Изображение в каждой позиции может быть специально настроено под конкретный вид представленной информации. Окно настройки изображений с двумя вкладками показано на рис. 3.

Установка параметров сечений

Установка параметров сечений

Координаты сечений Настройка изображений |

Координаты сечений | Настройка изображений |

Левое, верхнее: (• Равномерно

Л огарифмически

Размер ячейки:

Количество линий:

Левое, нижь

Равномерно

Правое, нижнее: (♦ Равномерно

Л огарифмически

Размер ячейки:

Количество линий:

Л огарифмически

Размер ячейки:

Количество линий:

Левое, верхнее: Координаты сече

По оси ординат:

Стиль поверхности:

<• FQ Г S

Левое, нижнее: Координаты сече

Правое, нижнее: Координаты сече

По оси ординат:

Стиль поверхности: Г FQ (• S

По оси ординат:

Стиль поверхности:

FQ

S

Рис. 3. Две вкладки окна настройки изображений в позициях окна эксперимента

С его помощью в каждой позиции окна эксперимента можно изменять размер сетки измерений (до 100×100), шкалу нарезки линий уровня (равномерная или логарифмическая), количество основных линии равного уровня. Любой участок изображения может быть многократно увеличен с помощью инструмента «Лупа».

Для многомерных задач с помощью вкладки «Координаты сечений» (на рис. 3 показана справа) можно дополнительно выбирать группы из пар переменных, по которым в данной позиции будет выбрано сечение для построения линий равного уровня указанной функции. Сечение проводится через точку текущей позиции. Текущая позиция отображается во всех сечениях в виде красной жирной точки. Её положение изменяется либо щелчком левой кнопки мыши по изображению, либо в процессе работы численного метода.

Для исследования задачи имеется также панель числовой информации, которая показана в правой части окна эксперимента на рис. 2. При изменении положения точки текущей позиции все данные панели пересчитываются. При изучении структуры задачи важным является индикатор знакопределённости Ґ k-1 матрицы Гессе вспомогательной минимизируемой функции в точке текущей позиции (используется символика Ґ k-1 > 0, Ґ k-1 < 0, Ґ k-1 <> 0). Перемещая точку текущей позиции с помощью мыши, можно исследовать изменение знакоопределенности.

На числовой панели (см. рис. 2) отображается следующая информация: номер шага; координаты текущей точки; текущее значение коэффициента штрафа; заданная точность поиска; значение целевой функции f в текущей точке; значение вспомогательной минимизируемой функции S в текущей точке; значение невязки по ограничениям; значение нормы антиградиента минимизируемой функции, вычисленного на текущем линейном многообразии поиска (с учетом двусторонних ограничений на переменные); значения первых компонент этого вектора после нормировки; значения первых компонент нормированного вектора направления выбранного методом шага. При проведении расчетов с использованием методов второго порядка, а также квазиньютоновских методов, вычисляющих заменители матриц Гессе, в нижней части панели числовой информации происходит отображение матрицы Гессе и других матриц, используемых методом.

Для двумерных задач используется ещё два инструмента – это построитель изображений функций f, S или H в виде 3D-поверхностей (см. рис. 4), а также построитель одномерный сечений функции f и S, позволяющий визуально оценивать искривленность их поверхностей в различных направлениях. Для получения 1D-сечений достаточно на одном из изображений в окне эксперимента построить мышкой секущей отрезок. Сечения f и S отображаются разными цветами – красным и синим (см. рис. 5).

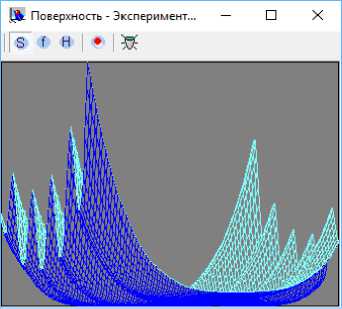
Рис. 4. 3D-изображение вспомогательной функции S γ (y, λ ) в методе модифицированной функции Лагранжа для задачи, показанной в окне эксперимента на рис. 2

Заметим, что постановка задач оптимизации в текущем окне эксперимента может быть легко изменена при включении специального режима редактирования задачи. При настройке задач часто ставится учебная цель получение задач такой структуры, чтобы они представляли сложности для исследуемых методов или конкретного метода.

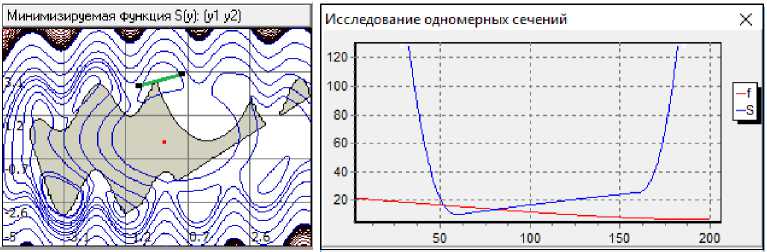
Рис. 5. Справа – вид одномерного сечения функций f(y) и S γ (y, λ ) вдоль секущего отрезка, выделенного зеленым цветом на картине линий равного уровня слева

Для исследования выбранных численных методов решения задач безусловной локальной оптимизации и методов учета ограничений используется дополнительный набор инструментов.

Выбранный численный метод можно применить к задаче, помещенной в текущее окно эксперимента. Перед запуском метода можно с помощью специальных диалоговых окон изменить значения уникальных параметров локального метода, а также набор его общих параметров и параметров выбранного способа учета ограничений. Также может быть назначен желаемый цвет изображения траектории.

Начальная точка запуска метода определяется выбором мышкой положения точки текущей позиции. Запуск метода возможен в трех режимах: пошаговом (каждый шаг – по нажатию специальной кнопки), в режиме «медленно» и в режиме «быстро». Во всех случаях рисуется траектория движения лучший (рекордной) точки, определённой методом. Для методов прямого поиска в пошаговом режиме и в режиме «медленно» дополнительно графически демонстрируются все промежуточные построения метода на шаге. В процессе счёта обновляется информация на числовой панели (набор отображаемой информации зависит от выбранного метода). Любой фрагмент изображений, включая траектории методов, может быть увеличен встроенной в программную лабораторию «лупой» с возможностью продолжения расчета в любом масштабе. В верхней правый позиции окна эксперимента дополнительно отображаются графики убывания рекордных значений текущей минимизируемой функции S γ (y) или S γ (y, λ ).

Каждое окно эксперимента запоминает результаты всех проведенных в нём расчётов в специальном архиве и отображает траектории всех проведенных в нём расчётов, а также графики убывания рекордных значений функции S γ (см. рис. 2).

В процессе проводимого расчёта окно эксперимента становится владельцем экземпляра выполняющегося численного метода, исполнение которого происходит в отдельном программном потоке. Это позволяет одновременно работать с разными запущенными расчётами в разных окнах экспериментов и переключаться между ними. Заметим, что поскольку при решении задач с ограничениями минимизируются функции S γ (y) или S γ (y, λ ), где параметры γ и λ могут автоматически изменяться, одновременно происходит пересчет и изменение линий уровня в соответствующих позициях окна эксперимента. Эти изменения может легко наблюдать пользователь.

После проведения расчётов окно эксперимента позволяет ретроспективно просматривать созданный им архив полных данных о всех проведенных расчётах. Для просмотра архива следует с помощью специальной кнопки переключить режим использования верхней правой позиции отображения в окне эксперимента. В новом режиме в этой позиции будут пошагово показаны сечения функций f и S в направлениях смещения рекордной точки для каждой из сделанных методом итераций. При этом с помощью специальных кнопок навигации по архиву расчётов (расположены на панели состояния внизу окна эксперимента) следует переключиться на нужный расчёт, а затем с помощью ползунка в верхней части блока отображения числовой информации выполнить переходы на нужные итерации (шаги) метода, как это показано на рис. 6.

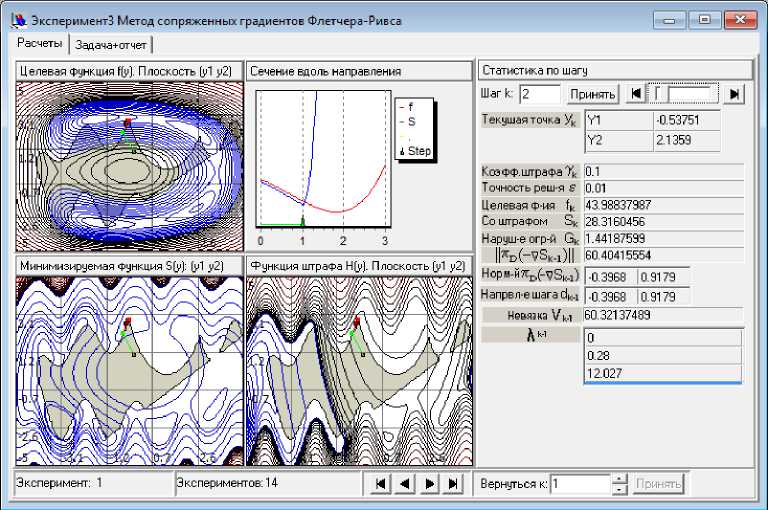
Рис. 6. Вид страницы «Расчеты» окна эксперимента в режиме просмотра из архива 1-го эксперимента; в верхней правой позиции области изображений показаны сечения функций f(y) и S y (y, X ) перед шагом 2 поиска методом Флетчера-Ривса минимума вспомогательной функции S у (y, X ) при у = 0.1

При этом на траектории расчёта будет ярко зеленым цветом выделен отрезок смещения на данном шаге, а в верхней правой позиции просмотра сечений f и S будет показано поведение этих функций вдоль данного отрезка и продолжающего его луча. При переходе от одного шага к другому пользователь будет наблюдать то же, что «видел» численный метод вдоль направлений смещений. Внимательный студент может получить при этом дополнительное представление о принципах работы численного метода.

В окне эксперимента кроме страницы по умолчанию «Расчеты» есть вторая страница «Задача+отчет», на которой находятся два многостроковых текстовых редактора. В верхний редактор автоматически записывается в текстовой форме постановка решаемой задачи и информация о выбранном численном методе. Во второй редактор помещается в виде наборов чисел полное описание траектории метода с результатами измерений вдоль траектории. Информация в редакторах доступна просмотру и редактированию, а также может быть отправлена в буфер обмена для формирования отчета по экспериментам. С помощью кнопок специальной панели инструментов в буфер обмена можно помещать любые изображения, построенные в окнах эксперимента.

При исследовании метода модифицированных функций Лагранжа для учета ограничений используются дополнительные инструменты наблюдения, указанные в следующем разделе.

Демонстрация использования LocOpt при изучении учета ограничений методом модифицированных функций Лагранжа

Покажем, как инструментарий программной лаборатории LocOpt позволяет проверить известные из теории факты, касающиеся метода МФЛ учета функциональных ограничений. В начале поясним концепцию исследования.

Наиболее простым методом учета ограничений является метод штрафов. Однако, при гладком штрафе сходимость к решению исходной задачи достигается только за счёт неограниченного возрастания коэффициента штрафа [1, 3, 8], что приводит к ухудшению структуры минимизируемой функции S γ (y) вспомогательных задач. В методе модифицированных функций Лагранжа квадратичный степенной штраф добавляется не к целевой функции f(y) исходной задачи, а к ее функции Лагранжа. За счёт этого у минимизируемой функции S γ (y, λ ) вспомогательных задач метода МФЛ появляется набор дополнительных настроечных параметров λ . Известно [2-4], что при достаточно общих условиях введение штрафной добавки с достаточно большим коэффициентом штрафа приводит к появлению у функции S γ (y, λ ) локальный седловой точки y^*, λ ^*, где y^* – является локальным решением задачи с ограничениями. Это пара находится методом МФЛ путем поиска локального минимума по y функции S γ (y, λ ^k) при заданном значении множителей Лагранжа. В результате определяется значение y^k+1. Затем метод выполняет шаг градиентного поиска максимума S γ (y^k+1, λ ) по переменным λ ≥0, применяя к каждой компоненте вектора λ известное итерационное соотношение. В результате вычисляется λ ^k+1. Далее процесс повторяется с возможным возрастанием коэффициента штрафа γ .

В LocOpt встроен режим автоматического управления коэффициентом штрафа и выбором момента остановки, исходя из поведения невязки V k = V( γ k , y^k+1, λ ^k+1) вдоль траектории поиска. V k является невязкой в системе условие оптимальности Куна–Таккера. При автоматической настройке γ k увеличивается в заданное количество раз, если значения V k убывают медленнее, чем указал пользователь, иначе γ k не изменяется. Можно проводить расчеты при фиксированном штрафе γ k .

Проведём исследование данного численного метода на задаче, графический и формульный вид которой представлен в окне конструктора на рис. 1. Задача имеет три функциональных ограничения–неравенства и восемь условных локальных минимумов. Исследуем самый верхний из них.

Вначале, используя математический пакет MatCad для прямого решения системы условий оптимальности выбранной задачи, приближенно определим для этого минимума пару y^*, λ ^*. Получим y^* = (-0.2765, 2.8147) и λ ^* = (0, 0.2800, 12.0272).

Воспользуемся возможностями графического отображения в LocOpt, чтобы убедиться, что при задании в S γ (y, λ ) значений λ = λ ^* линии равного уровня этой функции перестраиваются так, что в точке y = y^* возникает локальный минимум, если выбрано достаточно большое значение γ . Это показано на рис. 7. Был использован инструмент «Лупа» и малая окрестность локального минимума y^* увеличена в 20 раз. На рис. 7 видно, что ближайший локальный минимум S γ (y, λ ^*) существенно отклонен от y^* при γ = 0.1. Если же увеличить γ до значения 5, а затем до значения 10, то локальный минимум S γ (y, λ ^*) существенно приближается к точке y^*.

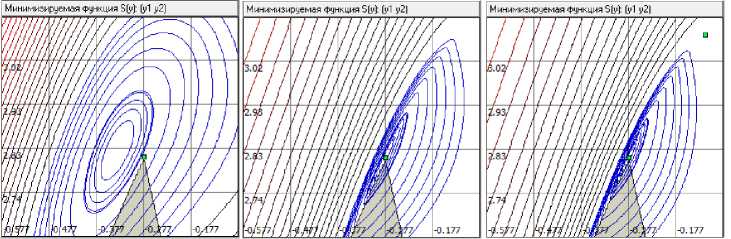
Рис. 7. Влияние увеличения у (слева направо: 0.1; 5; 10) на точность приближения условного локального минимума задачи положением локального минимума модифицированной функции Лагранжа S y (y, X ) при X = X *

Если же отклонить значение λ от λ ^*, то локальный минимум S γ (y, λ ) от желаемой позиции смещается, как показано на рис. 8. Например, при сохранении ранее рассмотренных значениях γ , но изменении множителей Лагранжа от λ ^* до значения λ = (0, 0.1, 3.0) локальные минимумы S γ (y, λ ) заметно удаляются от истинного положения условного локального решения задачи (отмечен зеленым маркером). Таким образом, подтверждаются известные из теории свойства метода.

Рис. 8. Влияние на положение локальных минимумов функции S y (y, X ) ( при значениях у слева направо: 0.1; 5; 10) отклонений множителей Лагранжа от оптимального значения X * до X = (0, 0.1,3.0)

Построим теперь траекторию метода МФЛ (см. рис. 9).

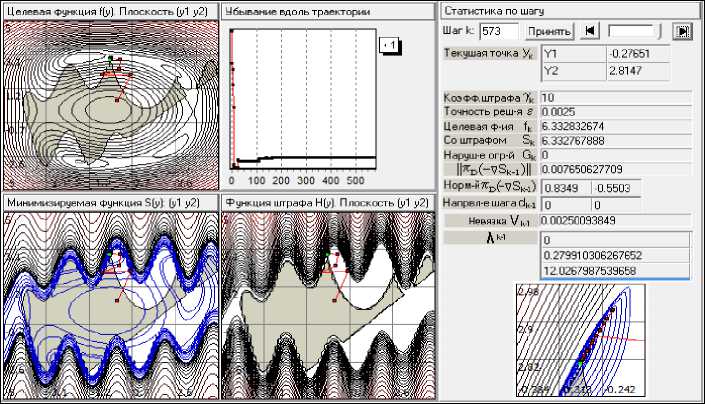
Рис. 9. Траектория и графики убывания функции S γ (y, λ ) в методе МФЛ

На рис. 9 расчет выполнен с использованием фиксированного коэффициента штрафа γ = 10 (траектория красного цвета) и c автоматической настройкой множителей Лагранжа. Начальное значение λ принято равным (0,0,0). Для поиска минимума каждой из вспомогательных функций S γ (y, λ ^k) использован метод Флетчера–Ривса. Расчет проведен при заданной точности (по невязке V k в системе условий оптимальности), равной 0.0025. Методу МФЛ потребовалось 48 основных итераций. На рис. 9 на нижнюю правую часть окна наложено увеличенное в 25 раз изображение окрестности найденной точки. Виден характер траектории, где сходимость оказалась обеспечена только настройкой множителей Лагранжа.

На рис. 10 приведено дополнительно включаемое для МФЛ окно наблюдения, показывающие графики изменения множителей Лагранжа и убывания невязки V k на 48 выполненных итерациях, соответствующих расчету на рис. 9.

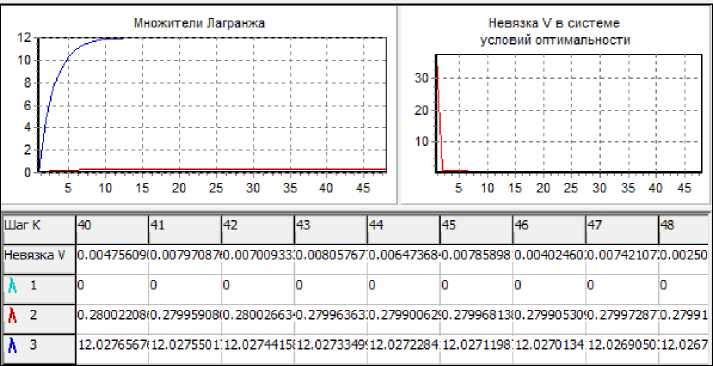
Рис. 10. Окно наблюдения за изменениями множителей Лагранжа λ ^k и невязки V k в системе условий оптимальности в процессе решения задачи методом МФЛ; числовая информация отображена на шагах с 40 по 48

Можно видеть, что y^k → y^*, а λ ^k →λ ^* с ростом k, что соответствует теории. Окончательное найденное решение y = (-0.27651, 2.8147) и λ = (0, 0.27991, 12.02680) , что соответствует невязке в системе условий оптимальности V k = 0.0025.

Заключение

Материал статьи основан на опыте преподавания численных методов математического программирования в бакалавриате прикладных и инженерных естественнонаучных направлений подготовки. Среди используемых при этом программных систем выделен специальный вид программного обеспечения – «программная лаборатория», отличающийся разнообразием предоставляемых средств и инструментов постановки и исследования изучаемых задач. Основные возможности показаны на примере учебно-исследовательской программной лаборатории LocOpt, ориентированной на наглядное экспериментальное изучение численных методов условный локальной оптимизации. Целесообразно многовариантное использование программных лабораторий в учебном процессе, как при организации лабораторных практикумов, так и в целях самообучения.

Автор считает, что по возможностям углубленного освоения численных методов математического программирования программные лаборатории типа LocOpt занимают промежуточное положение между программными тренажерами по численным методам и обучением через выполнение проектных заданий с самостоятельной программной реализацией численных методов. В то же время, исходя из опыта использования, программные лаборатории, по сравнению с проектным подходом, позволяют изучить материал более широко при меньшей затрате учебных часов. Таким образом, они являются эффективным инструментом освоения профессиональных компетенций в рассматриваемой предметной области.