Умумий ўрта таълим мактабларида тригонометрияни ўитиш методикаси

Кириш:

Мамлакатимизда таълим сифатини ошириш мақсадида таълим сохасида кўплаб ишлар олиб борилмоқда. Шу жумладан аниқ ва табиий фанлар бўйича иқтидорли ёш авлодларни етиштириб чиқариш уларни

қўллаб қувватлаш устивор вазифалардан бири қилиб белгиланган. Табиийки бу мактаб математика ўқув машғулотларига инновацион таълим технологияларини қўллаш, ривожланган хорижий давлатлар илғор тажрибаларидан фойдаланиш билан амалга оширилади.

Ҳозирги кунда тригонометрия, умумий ўрта ва ўрта махсус касб-ҳунар таълимида математика фанининг энг муҳим ва мураккаб бўлими хисобланади. Дастлабки тригонометрик тушунчалар мактаб математикасининг IX синф геометрия ва алгебра курсларида берилганлигини инобатга олиб, тадқиқотимимзнинг дастлабки қисмини мактабларда ўрганишни лозим деб топдик. Умумий ўрта таълим IX-X синф математика ўқув машғулотларини кузатиш ва ўрганиш натижасида ушбу синф ўқувчиларида тригонометрияни ўзлаштириш даражаси 50%-55% ни ташкил қилиши аниқланди. Ўлаштириш нима сабабдан паст даражадалигини аниқлаш мақсадида ўтказилган сўровлар натижасидан улар тригонометрияни мавхум тушунчалардан иборат деб хисоблашларини англаш мумкун.

Тригонометрия бу–тригонометрик функцияларни ва уларнинг геометрияга қўлланилишини ўрганадиган математиканинг бир сохасидир. Тригонометрия сўзи иккита юнонча: "trigwnon"-учбурчак ва "metrew"-ўлчов сўзларидан иборат бўлиб, учбурчаклар ўлчови деган маънони англатади.Қадим замонлардан бери айнан шу вазифа - бурчаклар ўлчови ёки учбурчак ечими, учбурчакнинг учта параметри берилиб қолган барча элементларини аниқлаш тригонометриянинг амалий қўлланмаларининг асосини ташкил этади.

Мактаб математика курсида тригонометрик функцияни киритишда узоқ йиллар давомида турли усуллардан фойдаланилган. Хозирда тригонометрияни алгебра курсида координаталар системасила олинган бирлик айлана ёрдамида киритилса, геометрия курсида тўғри бурчакли учбурчак томонлари нисбати орқали киритилади

Математика курсининг тригонометрия бўлими мазмуни ва ўқитиш методикасини такомиллаштириш бўйича М.Мартин, Ф.Дежарнетте, Ҳ.Гур, Н.Попов, В.Майер, илмий тадқиқот ишлари олиб боришган. М.Мартин, Ф.Дежарнетте ва Ҳ.Гур илмий-тадқиқот ишларида мактаб математика курсидаги тригонометрияни ўқитишнинг педагогик-психологик муаммолари тадқиқ этилган.

Рус математиглари Н.Попов ва В.Майер томонидан когнитив-визуал ёндашувга асосланган тригонометрияни ўқитиш методикасини компютер анимацияларидан фойдаланиб яратишган.Уларнинг ишларида асосий урғу алгебра ва анализ асослари курсида тригонометрик элементларни киритиш ва тригонометрик функцияларни ўрганишга қаратилган.

Умумий ўрта таълим математика курсини ўқитиш метододикаси бўйича С.Алихонов умумий ўрта таълим тригонометрия бўлимида жуда кўп айний муносабатлар, жумладан, қуйдаги муносабатлар ўрганилишини такидлайди:

• 1 .Тригонометрик функцияларнинг бирини иккинчиси орқали ифодалайдиган айний алмаштиришлар.

• 2 .Тригонометрик    ифодаларни    соддалаштиришдаги    айний

• 3 .Тригонометрик айниятларни исботлашдаги айний алмаштиришлар.

• 4 .Тригонометрик тенгламаларни ечишдаги айний алмаштиришлар.

алмаштиришлар.

Юқоридагилардан кўринадики, тригонометрия курсида айний

алмаштиришлар муҳим ўрин тригонометрик функцияларга тригонометрик функцияларни ўрганилади.

эгаллайди. IX синф геометрия таъриф берилганидан сўнг, ўзаро боғловчи қуйидаги учта

курсида тўртта айният

• 1.     cos²a + sin²a = 1;

• ².    ^ = . -a ;

• 3.    ctga = —. sina

sina

Бу айниятларни келтириб чиқариш геометрия курсида батафсил баён қилинган. Бу аўниятлардан яна қуйидаги учта айният келтириб чиқарилади:

1. tga • ctga = 1;

2. —1— = 1 + tg²a; cos² a

3. —1— = 1 + ctg²a. sm²a

Юқоридаги айниятлар тригонометрик ифодаларни ҳисоблашда бажариладиган айний шакл алмаштиришларда энг кўп қўлланиладиган айниятлар бўлиб ҳисобланади.

Ўқитувчининг вазифаси-ўқувчиларда тригонометрик билимни шунчаки ёдлаш йули билан хосил қилибгина қолмасдан ўқувчи онгида тригонометрик тушунчани англаган холда хосил қилишдан иборат.

Ўқувчилар айний шакл алмаштиришларни яхши ўзлаштиришлари учун биринчидан тригонометрик функциялар таърифини улардан бирини иккинчиси орқали ифодаловчи ва асосий айниятлар каби формулаларни билишларига, иккинчидан эса ана шу формулаларни тригонометрик ифода берилишига қараб тадбиқ қила олиш малакаларига боғлиқдир. Мактаб математика курсидаги айний шакл алмаштиришларни оғзаки бажаришга ўқувчиларни ўргатиш уларда мантиқий тафаккурни шакллантиради. Ўқитувчи бирор тригонометрик ифоданинг шаклини алмаштиришни бажаришдан олдин ўқувчиларга энг содда бўлган оғзаки тригонометрик машқлардан намуналарни доскага ёзиб, ўқувчилардан тезроқ оғзаки соддалаштиришни бажаришни талаб қилиши ўқувчиларни тригонометрик айният ва формулаларни эсда доимо сақлашларига имконият яратади.

Психологик ва педагогик тадқиқотлар шуни кўрсатадики, компютер графикасидан фойдаланиш ўқув математик материални нафақат муваффақиятли идрок қилишга ва эслаб қолишга ҳисса қўшади, балки, материалнинг моҳиятига чуқурроқ кириш имкониятини беради. Бу одатда аниқ фанларни ўзлаштиришда ишлайдиган миянинг чап ярим шари эмас, балки, иккала ярим шарнинг ҳам баробар ишлаши билан боғлиқ. Тақдим этилган маълумотни мажозий ва ҳиссий идрок этиш учун жавобгар бўлган ўнг ярим шар, визуаллик қилинганида фаол ишлай бошлайди.

Маълумки, интерфаол компютер графикаси функциялари визуал ва когнитив функцияларга бўлинган. Визуал функция электрон таълим ресурсларида чизмалар, диаграммалар, графикалар ва жадваллар кўринишида тақдим этилади. Когнитив функция эса тингловчилар ўрганилаётган объектларнинг математик моделларини ўрганиш орқали билим оладиган вазиятларда бўлади, чунки бу жараён фикрнинг интуитив ўнг мия механизмига асосланганлиги сабабли, билимнинг ўзи кўп жиҳатдан шахсий хусусиятга эга.

Ўқитилган тригонометриянинг барча ақлий операцияларини алоҳида босқичларга ажратишда, электрон таълим ресурси сценарийсини ишлаб чиқиш жараёнида алгоритмлаштирилмаган, мажозий тафаккур таркибий қисмининг ривожланишига ёрдам берадиган чоралар кўриш керак. Бунга электрон таълим ресурсини лойиҳалаш жараёнида фикрлашнинг ижодий таркибий қисмини мақсадли равишда янгилаб, таълим муаммоларини ҳал

қилиш имконияти қўйилса эришиш мумкин. Таълим жараёнида максимал таъсирга фақат миянинг чап ва ўнг ярим шарлари имкониятларидан математиканинг бир соҳасида мавжуд бўлган фан ўқитувчисини тайёрлаш технологиясидан фойдаланилганда эришиш мумкин.

Тригонометрия ўқувчилари ва талабаларини ўқитиш амалиётининг таҳлили шуни кўрсатадики, ўқитувчилар асосий эътибор мантиқий фикрлашга, яъни миянинг чап ярим шарининг ишига қаратилади. Психологлар томонидан олиб борилган тадқиқотлар натижасида одамлар олган маълумотларинингнинг 80% визуал канал орқали олганлиги аниқланди. Математикага келсак, К. Гаусснинг сўзларидан иқтибос келтириш ўринлидир: "Математика бу нафақат қулоқ, балки кўз учун ҳам илм"

Шундай қилиб, тригонометрия курсини қандай қилиб миянинг чап ва ўнг ярим шарларини бир мувозанатда ишлатган ҳолда ўқитишга эришиш керак деган муаммо пайдо бўлади.

Тафаккурни тўғри шакллантириш учун унинг психологик механизмлари ва ривожланиш йўналишларини тасаввур қилиш керак. Психологларнинг бу соҳадаги муҳим ютуқлари миянинг ярим шарлар аро ассиметриясини кашф қилиш билан боғлиқ. Чап ярим шарнинг иши одамга ёзма ва оғзаки нутқни тушунишга, грамматик жиҳатдан тўғри жавоб беришга, қатъий расмийлаштирилган белгиларни манипуляция қилишга ва рақамлар ва математик формулалар билан бемалол ишлашга имкон беради.

Ўнг

ярим шар инсоннинг онгсиз ижодий қобилиятларини ташувчиси, шунингдек график визуаллик асосида фазовий алоқаларни ўрнатиш, унинг объектдаги хусусиятларини таъкидлаш ва улар билан тасвирлар шаклида ишлаш қобилиятидир.

Адабиётлар таҳлили ва методологияси:

Б. М. Блуменфелднинг изланишлари тажрибали шахматчилар муаммоларни ечишда асосан позицияларда ҳаракат қилишлари тажриба сифатида кўрсатилган, яъни, у ёки бу шахмат фигурасининг шаклига эмас, балки бошқа фигуралар тизимидаги ҳолатига қараб фикрлайдилар. Худди шундай муваффақият билан улар шахмат муаммоларини нафақат фигураларни, балки уларнинг ўрнини босадиган нарсалар, яъни тошчалар ва бошқа шунга ўхшаш нарсаларни ишлатиб ҳам ечишлари мумкин. Муаммоларни ҳал қилиш бу ерда рақамларни ақлий равишда силжитиш орқали тўғри фазовий комбинацияни тезда топиш орқали таъминланади, бу асосан динамик фазовий муносабатларни акс эттирувчи аниқ тасвирнинг мавжудлигини англатади.

Aналитик ёндашувни талаб қиладиган вазифаларни ва арифметик операцияларни бажаришда чап ярим шар фаоллашади. Психологларнинг експериментал изланишлари шуни кўрсатдики, чап ярим шар сўзлар ва бошқа одатий белгилар, ўнг томон еса ҳақиқий объектлар тасвирлари билан ишлашга ихтисослашган.

В. С. Ротенберг таъкидлашича, тасвир элементларидан холи булган фикрлаш қуруқ, расмий бўлиб қолиш хавфини туғдиради. Бадиий тафаккурга умуман мурожаат қилинмайдиган таълим нафақат унинг ривожланишига хисса цушмайди, балки охир-оцибат уни сусайтиради. Ўқув материалининг образли томонига суянмаслик нафақат ўрганишни қийинлаштиради, балки баъзан ўқувчиларнинг ўқув материалини умуман тушунмасликларига хам олиб келиши мумкин.

Миянинг чап ва ўнг ярим шарларининг хусусиятларини биладиган ўқитувчи ўқув жараёнини янада самарали ташкил қила олади, чунки у визуал-мажозий ва OFзаки-мантикий фикрлашни мохирона бошцариш қобилиятига ега. Шуни таъкидлаш керакки, чап ёки ўнг ярим шари устунлик қиладиган одамларни қатъий равишда ажратиб бўлмайди, чунки улардан бири ёки бошқасининг иш хусусиятларининг фақатгина нисбий устунлигини фарцлаш мумкин холос.

Маълумотни тасаввур этишнинг икки усули (белгилар кетма-кетлиги ва расм-образлар куринишида) комбинацияси, улар билан ишлаш ва бир-бирини ифода этишнинг ҳар иккала усулини ўзаро боғлаш қобилияти инсон тафаккурининг аниқ феноменини таъминлайди. Визуаллаш тамойилининг асоси когнитив графика бўлиб, унинг мақсади тимсолий ва геометрик тафаккур усулларини бирлаштирадиган ва билиш фаоллашувига ҳисса қўшадиган билимларни намойиш етиш моделларини яратишдир. Фацат расм-образлардан фойдаланиш бошца бир салбий холат "фацат унг ярим шарнинг ишлаши"га олиб келмаслиги учун мацбул комбинация - бу ўқув жараёнида математик маълумотларни тақдим этишнинг ҳам визуал, хам огзаки усулидан хам оцилона фойдаланишдир

XXI асрда ахборотлаштириш жараёни жадал ривожланмоқда. Aхборот технологияларининг ривожланиши таълим соҳасида янги имкониятларни очиб беради: янги ўқув дастурларини жорий етиш, ўқув жараёнини замонавий шароитлар ва болалар ва уларнинг психикасининг умумий ривожланиш хусусиятларига мос равишда ташкил етиш имконини беради. Компютер технологияларидан у ёки бу шаклда фойдаланмайдиган ўқув муассасалари деярли қолмади десак муболаға бўлмайди.

Бундай технологияларнинг энг кенг тарқалган мисолларидан бири бу анимация. Математика дарсларида ўқитувчилар функсия графигини чизиш ёки геометрик фигурани ясаш учун турли хил воситаларни ва анимациянинг энг аниқ номойиш этадиган дастурлардан фойдаланишади. Бундай дастурлар қаторига " Живая математика ", "GeoGebra", "Maple"киради.

Математик дарсларда GeoGebra дастуридан фойдаланиш материални ўзлаштириш сифатини яхшилаш, ўқувчиларнинг иштиёқи ва қизиқишини оширишга ёрдам беради. GeoGebra динамик муҳитининг имкониятлари сизга визуал тасвирлардан тортиб тафаккур ва тасаввур тасвирларига қадар ўқувчиларнинг сезги идрокининг барча қаторини ўз ичига олган юқори сифатли анимацион ва тасвирий материаллардан фойдаланиш имконини беради.

Юқоридаги фикрларга таянган холда қуйидаги тригонометрик мисолларнинг ечимини аналитик усулда ва GeoGebra дастуридан фойдаланиб графикрафик усулда кўриб чиқамиз.

1.Тенгламани ечинг        ( 1+соs2x)sinx=cos²x

1+cos2x=2cos2x  формуладан фойдаланиб тенгламани қуйидаги кўринишга ўтказамиз cos2x(2sinx-1)=0  бундан

cos2x=0     sinx = 1

Қуйидаги натижаларга эга бўламиз

x = ^ + лк, keZ       x = (-1)n ^ + лп, neN

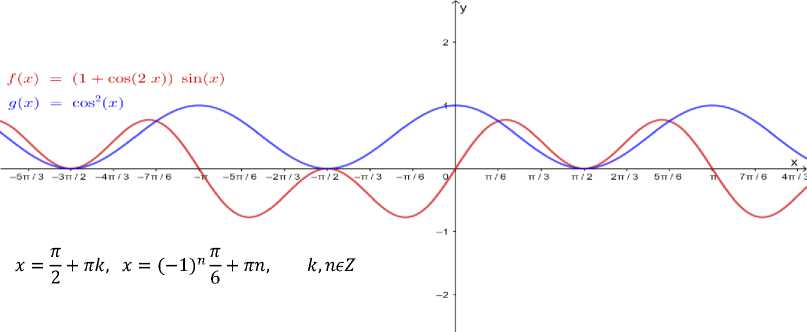
1-расм

Математикани визуаллаш ва уни янада кўргазмалироқ қилиш учун уринишлар узоқ вақт давомида амалга оширилган. Ҳатто қадимги математиклар энг оддий алгебраик идентификаторларни геометрик шаклда акс еттиришга ҳаракат қилишган. Кейинчалик Девид Хилберт, Леонард Ейлер ва Бернхард Риманн каби таниқли олимлар математикани оқилона тасаввур қилишни тарғиб қилдилар. "Математик тасаввур" ни ривожлантириш учун визуал ахборотни ташкил қилиш, ҳажм ва умумлаштириш даражасида оғзаки, оғзаки ифодаланган тушунчаларга мос келадиган визуал ахборотни ташкил қилиш, визуал математик концепцияларни шакллантиришга муттасил эътибор бериш керак. Математик жумлаларни исботлашда когнитив-визуал ёндашувни намойиш этадиган қуйидаги масалалар мисолида кўрамиз.

2-мисол arctg 1 + arctg 1 = 45° тенглик уринли эканлигини курсатинг

Тенлик ўринли эканлигини қуйидаги чизмада кўрсатиш мумкин

1 arctg -

1                    ^

arctg -

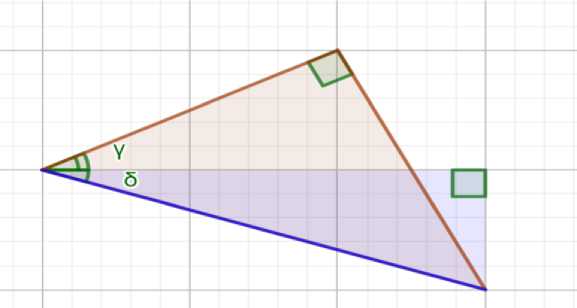
2-расм

3-мисол. Формулалар ўринли эканлигини кўрсаиинг

-    sin-

tg - =---- 7

2    1+cos-

= 1—cosP ^g 2      sin-

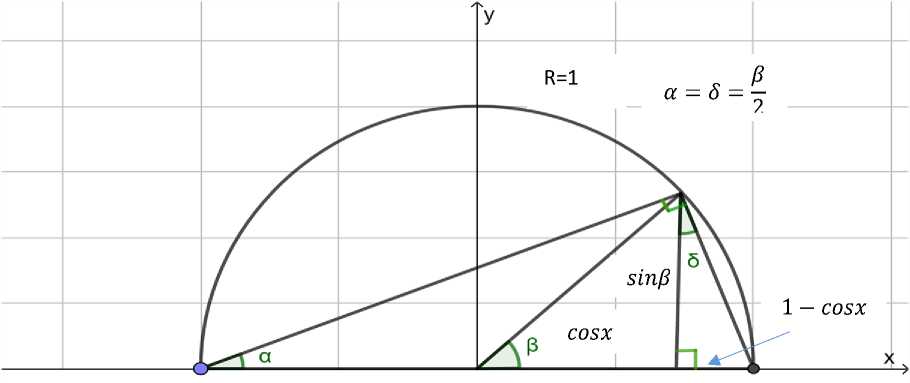
3-расм

Алгебраик билимларни геометрик жихатларини урганиш жараёнлари ва уларнинг реал воқелик билан боғлиқлиги Тригонометрия бўлиминини уцитишда уцув жараёнининг визуал-фигуратив таркибий цисмини, математикага боғлиқ бошқа фанларни кучайтиришга ёрдам беради ва математик маълумотларни цайта ишлашнинг фигуратив-ассоциатив усулидан максимал даражада фойдаланишга асосланган методик тизимларни ишлаб чициш масаласини хал цилади.

Табиийки, тасвирларнинг равшанлиги тригонометрияни ўрганиш жараёнини янада цизицарли цилади ва уцувчиларга мавзуни урганишга цизицишни уЙFOтишга имкон беради.

Ҳулоса:

Таъкидлаш жоизки, электрон таълим ресурсларининг ҳар бир ўқув елементининг визуал муҳити фаолиятининг асоси ўқув жараёнидаги "нисбатан тенг ва доимий" деб ҳисобланган ўқув математик маълумотларини тақдим этишнинг барча уч усулини битта "қурилиш" да цуллаш хисобланади.

• -    матн нафацат семантик (мазмун), балки визуал юкни (дизайнни) уз ичига олади;

• -    чизма концепциялар буйича хусусиятларни, узаро боглицлик ва операцияларни спекулятив намойиш қилишда, далилларга асосланган мулоҳазалар курсини визуал равишда намойиш қилишда, муаммони ҳал цилиш учун усулларни аницлашда фаол фойдаланилади;

• -    формула , математиканинг узига хос тили булган холда, огзаки тақдимотда бир нечта қоғоз ёки "экран" саҳифасини олиши мумкин бўлган теореманинг баёни ва исботини аниқ ва ихчам тарзда аниқлашга имкон беради.

Фодаланилган адабиётлар: