Umumiy o’rta ta’lim maktab matematika darslarida o’rganiladigan konsentratsiyaga va aralashmaga doir matnli masalalarni yechishni ba’zi tadbiqlari

Bu turdagi masalalar sanoatda, tibbiyotda va kundalik turmushda ham bir necha elementlardan muayyan proporsiyali qorishma, arlashma tayyorlash natijasida tug’iladi. Masalan, qurilishda qum va sement qorishmasi, xamir tayyorlanayotganida suv va tuz, tibbiyotda suv va spirt aralashmasini tayyorlash hamda ular shunchaki aralashma emas, balki ularning miqdori muayyan proporsiyada bo’lishi kerak. Shunday amaliy masalalarni yechish jarayonida asosiy tushuncha “kontsentratsiya” hisoblanadi.

Suvga tuz tashlasak, muayyan vaqt o’tgach tuz donalari suvda erib, tuzning suvli eritmasi paydo bo’ladi. Agar tuz massasi eritma massasining 11% tashkil qilsa, u 11% li eritma yoki konsentratsiyasi 11% bo’lgan eritma deb ataladi [1.82-83] .

Masalalarni yechish quyidagi tushunchalarni aniqlashtirishga asoslangan.

• -     moddaning aralashma massali kontsentratsiyasi

• -     moddaning aralashmadagi foizli kontsentratsiyasi

• -     moddaning aralashmadagi hajmli kontsentratsiyasi

• -     moddaning hajmli foizli kontsentratsiyasi

• 1)    Qaralayotgan barcha aralashmalar (qorishma, qotishma) bir jinsli.

• 2)    Sig’im birligi sifatidagi litr va massa birligi bir-biridan farqlanmaydi.

• 3)    Qorishma komponentlari o’rtasida kimyoviy va boshqa reaksiyalar mavjud emas.

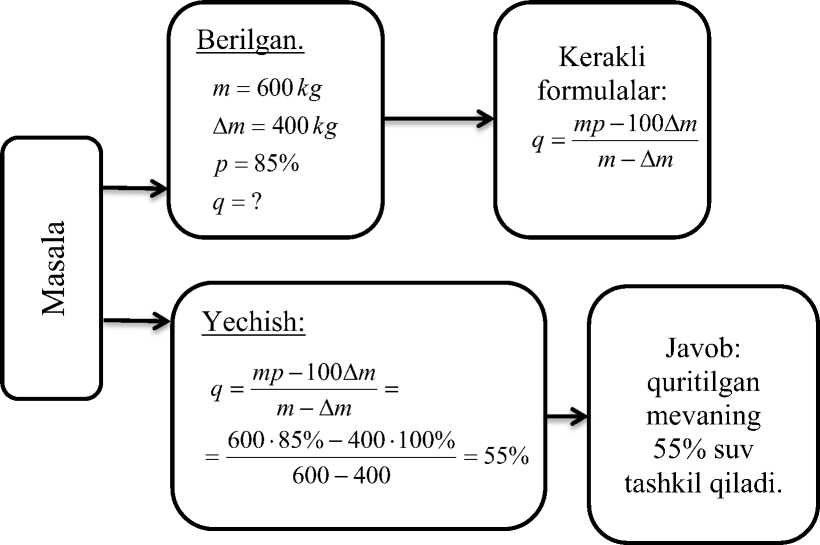
1-masala. Yangi uzulgan meva 85% suvdan iborat. 600 kg shunday mevani quritishda 400 kg suv bug’langan bo’lsa, quritilgan mevani necha foizini suv tashkil etadi?

Yechish: m va p bilan mevaning umumiy massasi va uning tarkibidagi suvning protsentli miqdori, Am esa bug’lantirilgan suv massasi bo’lsin. Quritilgan meva tarkibidagi qolgan suvning protsentli miqdorini q bilan belgilaymiz. Masalada q noma’lum. Yangi yig’ilgan mevada m^p miqdorda suv bo’ladi. Mevaning suvdan “ajratilgan” qismi massasi m - m—p ga teng. Bu quritilgan meva massasi m-Amning 100-q foizini tashkil etadi. Bu esa m -

m • p ( m -A m ) - ( 100 - q )

100 =        100

tenglikda ifodalanadi. Oxirgi tenglikdan noma’lum

q ni quyidagicha aniqlaymiz:

m^(100-p) = (m-Am)^(100-q )^q = ——100Am  hosil bo’lgan formula m - Am qo’yilgan masalani umumiy tarzda yechish formulasidir. Masala shartiga ko’ra berilganlarni yozib olamiz.

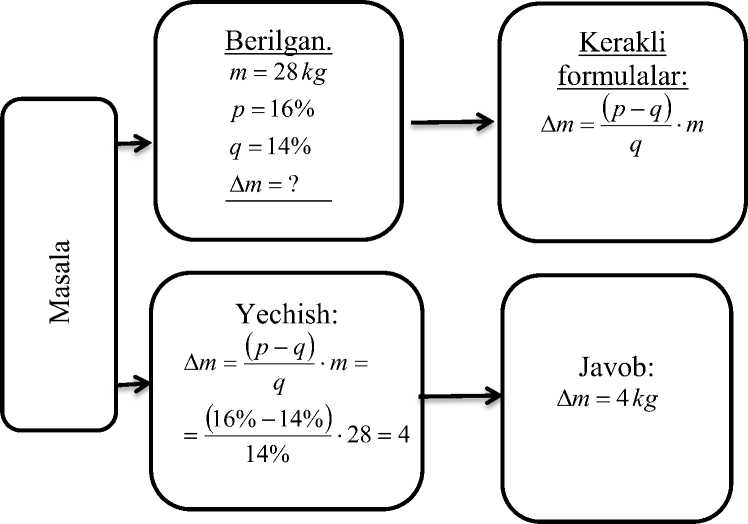
2-masala. 28 kg 16% li tuzli eritmadan 14% li tuzli eritma hosil qilish uchun unga necha litr chuchuk suv quyish kerak?

Yechish: Masalada eritmaning massasi m , konsentratsiyasi p ,qo’shiladigan chuchuk suvning massasi A m , chuchuk suv qo’shilganidan keying konsentratsiyasi q deb belgilaymiz va dastlabki eritmadagi tuz miqdori m • p 100

ga teng bo’ladi. Unda chuchuk suv qo’shilganidan keying massasi m + Am bo’lsin, eritmaning tarkibidagi

^{m + A m} tashkil etadi. Bundan

m • p tuz massasi m + Am eritmaning q foizini quyidagi ifodani keltirib chiqaramiz, ya’ni m + Am  m • p    .    m • p

=    ^ A m =    — m

100    100 q

q

- ( p - q ) ifodani soddalashtirsak, ^{A m} =----- , _q

• m

hosil bo’ladi. U holda masala yechimi hosil bo’lgan formuladan foydalanib topamiz.

3-masala. Agar 8 foizli 4kg eritmani 6 foizli 3kg eritmaga aralashtirilsa, necha foizli eritma hosil bo’ladi?

Yechish: Berilgan masalani quyidagi tartibda yechishni amalga oshiramiz. Dastlab birinchi eritmani massasini m , konsentratsiyasini p , ikkinchisinikini n va q bilan belgilaymiz. Ikkala aralashmadan hosil bo’lgan eritmani massasini m + n

m • p

va undagi tuz miqdorini topish uchun birinchi eritmadagi tuz miqdoriga n • q m • p + n • q ni yig’indisiga teng 100

ga, ikkinchi eritmadagi tuz miqdorini 100

m • p + n • q bo’ladi. Endi esa massasi 100 ga teng bo’lgan tuz massasi m + n ga teng bo’lgan eritmaning necha foizini tashkil etishini topishimiz kerak unda ikki eritmani aralashtirishdan hosil bo’lgan eritmaning konsentratsiyasini r deb m •p + n • q • 100

100         _m • p + n • q _m • p + n • q belgilab, r =     m+n     = m + n , r = m + n hosil qilamiz.

Adabiyotlar:

"Экономика и социум" №5(84) 2021