Влияние дисперсной фазы гетерофазных модельных пищевых систем на летальность при финишной стерилизации

Введение. Изучение теплообмена в упаковках с гетерофазными консервируемыми продуктами при их финишной термической стерилизации необходимо для установления температурного режима в их наименее прогреваемых зонах (англ. Slowest heating zone SHZ) и расчета стерилизующего эффекта, обеспечивающего их микробиологическую безопасность для потребителей и стабильность при обороте [1].

Результаты исследований гетерофазных модельных FS показывают, что SHZ локализована в зоне первого нижнего слоя дисперсной фазы, в которой следует проводить исследования летальности [2].

Для прогнозирования изменения температуры в измельченных пищевых продуктах (рис. 1), аналогичных исследованным FS [2], в [3] по результатам прогревов предложено использование математической модели термограмм (формула (1)) и ее функциональной интерпретации для анализа теплопередачи в гетерофазных продуктах.

а

Рис. 1. Гетерофазные модельные системы и их термограммы в фазе нагрева: а – модельные FS в банках по 300 мл с термопарами, исследованные в [3];

б – термограммы прогрева модельных FS по [3]

С И-------------1--------------1--------------1-------------1-------------1--------------1-------------7-------------1-----------

О    5   10   15   20   25    30   35    40

Time (min)

Figure 2.a. Experimental TTiermal History in Cylinders, (o) Retort. (■) 0.01 in. (0) 0.015 m. ( A) 0.02 m

б

Модель температуры t FS по формуле (1), по мнению авторов [3], позволяет рассчитать t модельной FS и продолжительность стерилизации ф , необходимые для обеспечения инактивации целевых микроорганизмов.

Формула (1) расчета безразмерной температуры и(ф) определяет сигмовидный характер изменения температуры t(ф) таких FS при нагреве и охлаждении

Ы _ t . -I- ^st и⇔ = + ф A~x , (1) tst Co 1+exp^L— где tst – температура среды в стерилизаторе, °С; t0 – температура FS в начале процесса стерилизации, °С; х – время установления ф =(фst +фp)/2, мин; d – параметр темпа изменения t(ф) при ф = x, мин; фА – псевдоначаль-ное время нагрева [4], мин.

В формуле (1) использованы параметры x, d, ф А из известного «формульного» метода (англ. Formula Method – Ball&Olson) расчета летальности Болла [4] и его модификации по [5], учитывающей разный характер и темп фазы нагрева d в стерилизаторе до температуры t st . Параметры можно получить только эмпирически для частных условий стерилизации теплопроводной теплопередачей, поэтому они не подходят для обобщенного расчета летальности.

На термограммах фазы нагрева (рис. 1, б ) в центре банки с модельными FS выделяются два участка: первый от начала до time = 4 min, на котором температура FS t = 22 °C, второй с экспоненциальным ростом температуры t до t st ≈ 118 °С по [3]. Метод расчета режима по стерилизующему эффекту приведен в [5].

Подробное исследование летальности в близких по свойствам FS приведено в [6], в котором метод расчета летальности также основан на анализе эмпирических данных из экспериментальных прогревов FS в изотермических лабораторных и промышленных условиях с разными значениями начального участка термограмм, которые в «формульном» методе [4] относят к псевдоначальному времени ф А и соответствующей ему псевдоначальной температуре t A , и более совершенный метод с использованием функции Бесселя [7].

Эти расчеты, несмотря на сложный алгоритм, связанный с введением псевдоначальных значений ф А , t A [4], исходят из экспоненциального характера термограмм фазы нагрева FS при финишной термической стерилизации, независимо от характера теплопередачи в FS. Такая парадигма соответствует теории регулярного теплового режима, по которому проходят основные этапы нагрева и охлаждения FS [8–11].

В настоящей работе проанализирован характер термограмм изотермического нагрева и охлаждения трех гетерофазных FS при t st = {75, 80, 85, 90, 95} °С.

Цель исследований – получить и проанализировать экспериментальные данные температуры и летальности в наименее прогреваемой зоне (SHZ) гетерофазных модельных FS при изотермической стерилизации для установления функциональных зависимостей температуры t(ф) FS и летальности F (t) .

Задачи: установление значений динамических характеристик и тепловой инерции гетерофазных FS в стеклянных банках для определения характера процесса теплопередачи в них при термообработке и использования данных в расчетах термоинактивации и режимов финишной стерилизации целевых микроорганизмов в гетерофазных FS.

Объекты и методы . Объектами исследования были модельные FS, в которых дисперсная фаза – шары из стиролакрилонитрила (англ. Styrene-acrylonitrile SAN) Ø8 мм с плотностью с = 1,67 г/см³, теплоемкостью С = 2000 Дж/кг·К и теплопроводностью л = 0,13 Вт/м·К.

Для сравнения влияния свойств дисперсионной среды в исследованиях использовали пищевые жидкости с различной вязкостью м : маловязкий водный раствор концентрацией по

• 1,5 % сахара и соли (FS1), сок яблочный осветленный восстановленный для детского питания с 11,2 % рсв (FS2) и сахарный сироп с 11 % рсв (FS3). Модельные FS дозировали в стеклянные банки вместимостью нетто 190 мл с венчиком горловины III типа, где масса шаров в каждой модельной системе составляла 174,4 г, а дисперсионную среду добавляли в банки до общего объема FS 190 мл.

Измерения температуры FS в экспериментах проводили игольчатой термопарой Ellab Ø1,2 мм градуировки MK(Т) с фиксированной высотой h ее нижнего конца от дна банки по оси (рис. 2).

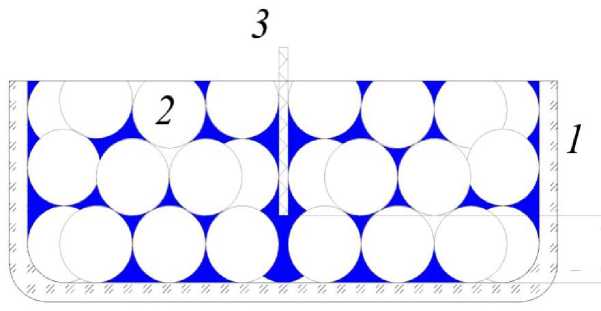
Рис. 2. Банка с модельной FS и термопарой:

1 – банка 190 мл; 2 – шары NAS; 3 – термопара Ø1,2 мм

Эта высота h = 7 мм (рис. 2) соответствует локализации SHZ в указанной банке при стерилизации FS1÷ FS3 [2]. Кроме этого, необходимо расположить измерительную часть термопары 3 (рис. 2) в пространстве между шарами 2, не касаясь их, исключив погрешность теплоотвода от термопары к шарам. Высота свободного пространства в банке до крышки составляла 20 мм. Регистрировали температуру FS в SHZ восьмиканальным автоматическим термометром Ellab CTF 9008 с погрешностью ± 0,1 °С и дискретностью по времени 30 с, подключенным через COM порт к РС.

Предварительно термостатированные при t0 = 30 ± 0,1 °С банки с FS1 ÷ FS3 нагревали при пятикратной повторности в водяном циркуляционном термостате WCH-16 с постоянными значениями температуры tst={75, 80, 85, 90, 95} °С в течение 20 мин и немедленном охлаждении в непроточной воде 10 мин при температуре охлаждающей воды tw = 21 ± 0,1 °С.

Математическую обработку экспериментальных данных прогрева и охлаждения FS проводили с использованием ПО Ellab, программы аппроксимации графиков Table Curve 2d v.5.01 (SYSTAT Softwarelnc) [12].

Результаты и их обсуждение. В результате экспериментальных прогревов и обработки термограмм получены средние значения t(ф) по выборкам из прогревов в пятикратной повторности трех FS при изотермическом нагреве в одинаковых условиях, с заменой образцов заливки модельных FS при каждом прогреве.

Термограммы FS1 при разных t st можно разделить на 4 однотипные области (рис. 3).

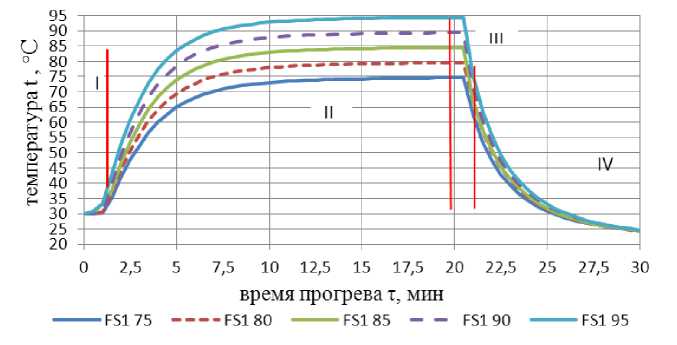
Рис. 3. Термограммы по средним значениям температуры FS1 t в SHZ (h = 7 мм) из 5 прогревов при различных t st

Первая обозначена (I), от погружения FS1 в термостат при ф = 0 до ф ≈ 1 мин. В области (I) t(ф) = t 0 = const, что соответствует иррегулярному тепловому режиму начала прогрева [13].

Вторая область (II) при ф = 1 ÷ 20 мин ∀ t st , в ней термограммы представляют собой почти идеальные экспоненты с постоянной времени Т = 2,468 мин, рассчитанной аппроксимацией значений t(ф) в этой области при помощи программы Table Curve 2. Эти части термограмм соответствуют модели регулярного теплового режима [13] при теплопроводном прогреве в FS.

Формы областей I и II термограмм аналогичны приведенным термограммам с другими модельными FS, содержащими шары из другого материала и разных размеров, другую дисперсионную среду и другие размеры упаковки [3]. Это означает, что основу полученных моделей процесса теплопередачи можно распространить на гетерофазные FS с аналогичным составом компонентов и упаковки [13].

Третья область (III) ф = 20 ÷ 21 мин, начинается на двадцатой минуте при переносе банки с FS1 из термостата в охлаждающую воду с t w =21°C. Эта область, как и (I), при нагреве соответствует иррегулярному тепловому режиму при t ≈ const , близкой к t st [13].

Четвертая область (IV) ∀ ф ≥ 21 мин, экспоненциального снижения t и также соответствует модели регулярного теплового режима охлаждения тела теплопроводностью [13]. Независимо от начального перепада t st - t w конечная температура t FS при ф = 30 мин, t 30 ≈ 24,5 °С, что указывает на характерную роль температуры FS в исследованиях термического эффекта стерилизации, а не летальности F .

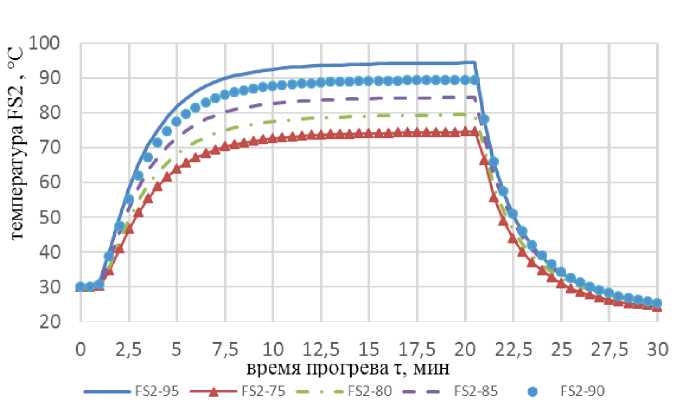
Рис. 4. Термограммы по средним значениям t в SHZ (h = 7 мм) из 5 прогревов гетерофазной FS2 при различных t st

Приведенные на рисунке 4 термограммы прогревов FS2 также можно разделить на четыре аналогичные области с такими же, как и у термограмм FS1 (рис. 3), количественными параметрами, несмотря на то, что дисперсионная среда FS2 – это сок яблочный осветленный восстановленный с содержанием рсв 11,2 %, по сравнению с FS1, у которой содержание рсв дисперсионной среды равно 2,5 %, меньшее значение плотности с ( с сока = 1,05кг/м³, с FS1 = 1,025 кг/м³ при температуре 30 °С) и вязкости м .

Термограммы прогревов FS3 аналогичны термограммам модельных FS1 и FS2 за исключением «зубца» температуры величиной Дt = + 0,5 °C в начале фазы охлаждения, который обусловлен незначительными механическими колебаниями банки с FS при переносе ее из термостата в охладитель.

Аппроксимация термограмм (рис. 3, 4) для зон регулярного теплового режима II выполнялась экспоненциальной функцией, когда на термограммах отмечалось монотонное изменение t(ф) . Аппроксимирующая функция t(ф) гетерофазных FS, пригодная для расчетов и моделирования, имеет вид

t(ф) = ^0 +( ^st ^- ^0 ) × (1 - exp(-ф/T)). (2)

Показатели тепловой инерции Т экспоненциальных зон термограмм FS2 в формуле (2) имеют близкие значения к аналогичным показателям FS1. Но, как и у FS1, показатель тепловой инерции зоны экспоненциального охлаждения Т охл ≈ 3 мин, что больше, чем у зоны нагрева ( Т ≈ 2,5 мин), поскольку охлаждение проводилось в спокойной воде, а нагрев в термостате с интенсивным перемешиванием воды, так как при этом коэффициент теплоотдачи от воды к банке при охлаждении меньше, чем при нагреве.

На основании средних значений выборки из пяти повторностей данных термограмм (рис. 3, 4) по формуле (3) из [1] определены значения летальностей F(ф) для модельных FS1 ÷ FS3

_.. . £ ^ref

F(ф)= ∑^ф(Δф × 10 ^z ) , (3)

где t ref – референтное значение температуры для сравнения летальностей F , °C; z – изменение температуры t, приводящее к десятикратному изменению F, °C.

Для стерилизации FS при температурах t st ≤ 100 °C принимали t ref = 80 °C, a z = 15 °C.

Результаты обработки данных прогревов в пятикратной повторности для каждого значения температуры каждого вида модельной FS показаны на приведенных графиках летальностей F(ф) (рис. 5).

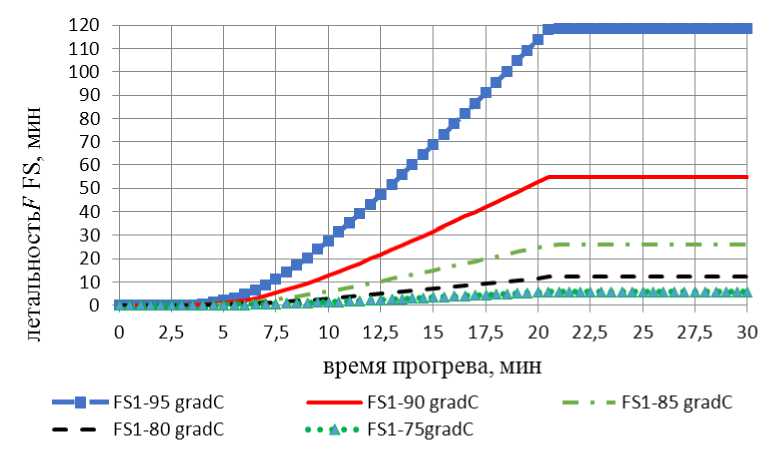
Рис. 5. Зависимости средних по выборке летальностей F(ф) гетерофазной FS1 в SHZ для разных значений t st

Графики летальностей F(ф) для FS1 ÷ FS3 аналогичны и количественно отличаются только по температуре t st . Из рисунка 5 видно, что кумулятивная летальность F(ф) увеличивается только в фазе нагрева, а при охлаждении постоянна, так как температура t FS при охлаждении быстро снижается из-за большой начальной разности t(ф) – t w . При этом F нелинейно увеличивается с ростом t(ф) , поэтому для аппроксимации летальности F(t) использована показательная функция температуры t.

Аппроксимирующая показательная функция F(t) с основанием 10 феноменологически наиболее подходит для анализа, так как структурно совпадает с формулой расчета летальности (3).

При аппроксимации с r² = 0,9999 по Table Curve 2d при z = 15 °С функции имеют вид

_ 10 1. О 74+(t-80)/z

= 10 1 . О 6+(t - 8 0 )/z

FfS2

Ffs3

= 10 1 . О 6 9+( t - 8 0)/z

Функциональные зависимости летальностей F(t) FS1, FS2 и FS3 (4)–(6) незначительно различаются между собой. Ниже на рисунке 6 показаны в полулогарифмических координатах сводные экспериментальные зависимости летальностей F(t) FS1, FS2, FS3 от t st . Они имеют вид параллельных прямых линий, как и аппроксимирующие функции (рис. 6).

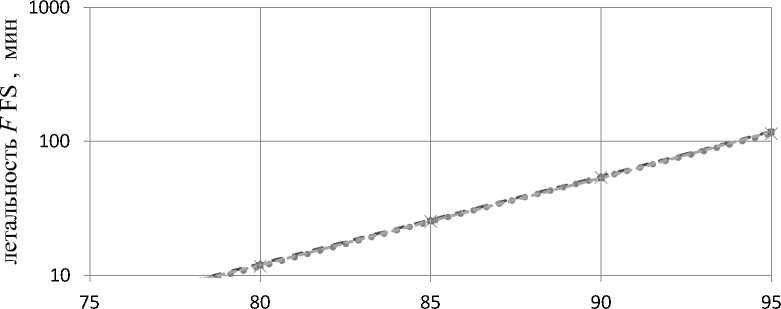
температура стерилизации tst, °C lethality FS1              lethalityFS2              lethalityFS3

Рис. 6. Зависимость летальностей F(t) в SHZ трех исследованных FS от температуры t st

На рисунке 6 прямые F(t st ) для гетерофазных FS1, FS2, FS3 с неподвижной дисперсной фазой в течение всего процесса стерилизации практически сливаются. При этом дисперсионные среды в них (яблочный сок, заливка и сироп) существенно различаются по плотности с , вязкости м , которые в соответствии с теорией термогравитационной конвекции являются основными факторами, определяющими конвективный характер теплопередачи в FS.

Следовательно, установленный нами в экспериментах одинаковый характер термоинактивации в таких исследуемых гетерофазных FS определяется только одинаковыми дисперсными фазами (шариками), и его следует рассчитывать по закономерностям теплопроводности.

Заключение. Теплообмен в гетерофазных FS, содержащих не вовлекаемую в конвекцию дисперсную фазу из большого числа твердых частиц, зависит преимущественно от теплофизических свойств дисперсной фазы.

Характер и теплоинерционные параметры процесса термической стерилизации таких FS не зависят от свойств жидкой дисперсионной среды и характера теплообмена в ней и определяются по закономерностям теплопроводности.

Экспоненциальная функция температуры в SHZ от времени с запаздывающим аргументом с достаточной точностью моделирует термограммы гетерофазных FS при финишной изотермической стерилизации.

Эмпирическая зависимость летальности гетерофазных FS от температуры стерилизации соответствует показательной функции с основанием 10, как и формульное значение летальности.