Влияние портфолио на качество освоения математических дисциплин

студентов и самообучаться. При этом учитывались также их посещаемость, успеваемость и промежуточная аттестация. Анализ результатов показал, что идеальной технологии не получается, т.к. на разных этапах процесса обучения роль видов СРС меняется очень сильно: отдельные виды СРС из разряда «важных» они плавно перетекают в «неважные» и наоборот. Аналогично обстоят дела и с нормативным подходом, т.к. реформы в образовании идут практически непрерывно. Поэтому в данной статье остановимся на создании реальной модели обучения. На современном этапе образования используются различные инновационные подходы к обучению3, среди которых наиболее распространенными являются информационные технологии4 в подготовке, бакалавров, специалистов, магистров, а также система персонифицированной профессиональной подготовки студентов, подстраивающаяся под личностные факторы индивидуума5. Одним из новых подходов в обучение является формирование портфолио, которое может стать существенным элементом модернизации российской выс- шей школы6. Формирование портфолио – это глубокий систематизированный самоанализ, требующий серьезной аналитической деятельности, осмысления своего опыта, накопления результатов и активизация СРС7. Как отмечает, Е.В.Шах-матов 8 в современных условиях стремительно меняются технологии и требования к выпускникам вузов и нет времени на долгую адаптацию на производстве. Именно портфолио, может стать тем инструментом, как указано в коллективной монографии под редакцией О.Г.Смоляниновой9, который ускорит адаптацию выпускника к послевузовской деятельности в самом широком смысле.

Однако, отмечая целый ряд исследований применения портфолио в педагогической практике 10 необходимо все-таки отметить, что их результаты недостаточно формализованы, поэтому не позволяют прогнозировать качество освоения учебного материала, например при сочетании портфолио с другими видами СРС и характеристиками организации учебного процесса. В связи с этим целью данного исследования является разработка модели влияния технологии портфолио на активизацию СРС и качество освоения блока математических дисциплин.

Изменились требования 11 к результатам освоения программ в виде компетенций. В ФГОС ВПО содержались только общекультурные (ОК) и профессиональные (ПК), а ФГОС ВО предусматривает еще и общепрофессиональные (ОПК) компетенции. Общее число их сохранилось, однако вуз имеет право дополнить набор компетенций и требований к результатам обучения по отдельным дисциплинам или практикам самостоятельно, что позволяет студентам получить углубленные знания и навыки для успешной профессиональной деятельности или обучения в аспирантуре. Это дает возможность иметь каждому обучающемуся свой индивидуальный маршрут следования на длинном пути освоения образовательных программ бакалавриата, магистратуры и аспирантуры, т.к. математические знания необходимы при изучении практически всех дисциплин направления подготовки «бизнес-информатика», то вопрос качества освоения блока математических дисциплин стал одним из центральных смыслообразующих вопросов исследования. При этом необходимо на основе анализа результатов анкетирования 49 респондентов ППС по действующей системе обучения по ФГОС ВПО, названное в статье «как есть» и по системе «как должно быть» (по ФГОС ВО): 1) Проанализировать степень взаимосвязи между переменными (проверка мультиколлинеарности) и взаимосвязи переменных-предикторов с зависимой переменной Y с помощью парных коэффициентов регрессии. 2) Отобрать наиболее существенные объясняющие переменные. 3) Найти уравнения связи с оставшимися переменными. 4) Определить степень точности полученной модели.

Исследование многофакторное. Из таб. 1 видно, что ППС требовательно относиться к факторам «посещаемость занятий» и «успеваемость», т.к. важность параметра отмечается в 100% анкет. Хотя в настоящее время абсолютно удовлетворены посещаемостью студентов лишь 39,13%, а успеваемостью 21,74%. Следовательно, категория лучших студентов «могут и хотят» составляет примерно четверть обучающихся. Полностью удовлетворены по данным параметрам – 39,13%, и 56,52% соответственно, частично – 13,04%, а оставшиеся 8,70% – это те из студентов, которых можно отнести к категории «не могут и не хотят» учиться, следовательно, им не место в высшем учебном заведение, что объясняет отчисления студентов. Можно, таким образом, констатировать факт, что сегодняшнее стремление министерства образования к уменьшению числа вузов и поднятию престижа высшего образования оправдано.

Таб.1. Сравнение ответов ППС

Сопоставимый фактор	Удовлетворенность ППС в системе «как есть», %				Требовательность ППС в системе «как должно быть», %
	Абсол	Полно	Част	Не удовл	Важно	Не важно
1. Исследовательское задание	13,0	21,7	30,4	34,9	100	0
2. Опубликование статьи	65,2	26,1	8,7	0	100	0
3. Выступление на научной конференции	26,1	30,4	39,1	4,3	95,7	4,3
4. Аудиторные контрольные работы	21,7	52,2	17,4	8,70	82,6	17,4
5. Домашние контрольные работы	13,6	31,8	27,2	27,2	78,3	21,7
6. Работа над ошибками аудиторной КР	8,7	30,4	30,4	30,4	87,0	13,0
7. Работа над ошибками домашней КР	8,7	30,4	13,0	47,8	82,6	17,3
8. Проведение коллоквиума	17,4	8,7	34,8	39,1	82,6	17,4
9. Устный ответ студента с места	17,4	52,2	8,7	21,7	78,3	21,7
10. Работа студента у доски	21,4	34,8	17,4	26,1	78,3	21,7
11. Выступление с докладами на занятиях	21,4	43,5	26,1	8,7	91,3	8,7
12. Проведение промежуточной аттестации	13,0	43,5	30,5	13,0	95,7	4,3
13. Формирование портфолио	8,7	8,7	26,1	56,5	87,0	13,0
14. Посещаемость занятий	39,13	39,13	13,04	8,7	100	0
15. Успеваемость	21,74	56,52	13,04	8,7	100	0

Отдельно остановимся на факторе «формирование портфолио». Более половины опрошенных респондентов 56,5% в лице ППС, по всей видимости, не используют сегодня данную форму обучения, активизирующую СРС. В тоже время 87% ППС по системе «как должно быть» отметили важность фактора, что указывает на то, что преподаватели готовы, а значит, знакомы теоретически с данным подходом в обучении. Следовательно существует большой резерв повышения качества освоения образовательных программ обучающимися при переходе на ФГОС ВО, рекомендующие применение портфолио как способ активизации самостоятельной работы студентов.

Аналогично проанализируем данные относительно других параметров исследования. При введении портфолио возрастает возможность проводить промежуточную аттестацию, организованную деканатом на 6, 10 и 14 неделях обучения. По системе «как есть» 13% респондентов считают ее важной, причем 43,5% удовлетворены ее проведением, третья часть удовлетворена лишь частично, а 13% считают ее ненужной. Следовательно, более половины ППС считают, что ее проведение деканатом можно улучшить, либо она не приносит никакой пользы. А вот по системе «как должно быть», уже 95,7% считают ее возможно успешной, признавая, что контролируемый ход ведения портфолио дает возможность объективно выставить как количественную так и качественную оценку.

Анализируя результаты анкетирования по параметрам «исследовательское задание» (100%), «опубликование статьи» (100%), «выступление на научной конференции» (95,7%), «выступление с докладами на занятиях» (91,3%), видим, что творческие виды СРС приобретают более важное значение при личностно-ориентированном подходе к обучению. Именно они помогут студентам из категории: могут, но не хотят. Эмоциональный настрой, с которым студент осваивает в вузе ОК, ОПК и ПК и формирует собственный портфель достижений, в значительной мере определяет эффективность всей его учебной деятельности, а также существенно влияет на уровень работоспособности.

Осталась последняя категория студентов, которые не могут, но хотят учиться. Составив индивидуальную образовательную траекторию и выбрав посильные задания, они смогут учиться дальше, т.к. любое обучение представляет из себя цикл, состоящий из повторяющихся действий, то им захочется перейти на новый, более высокий уровень. И делать это они будут с постоянно возрастающим энтузиазмом. И чем дальше, тем больше есть возможность развить свой потенциал, добиться успеха при изучения блока математических дисциплин.

Таким образом, проведя социологический анализ результатов анкетирования ППС, получены данные для построения линейной модели множественной регрессии процесса обучения, использующего формирование портфолио, позволяющего активизировать самостоятельную работу студентов. Выбор факторов, влияющих на процесс обучения не должен превышать одной трети объема имеющихся данных, т.е.

т < 7, (1), где n – количество анкетируемых, m – количество факторов. Т.к. в выборке участвовало 49 человек ППС, то факторов может быть не более 16. Пусть *1- *2..... *13- *14- *15 – рассмотренные параметры (таб. 1): исследовательское задание, опубликование статьи, ..., формирование портфолио , посещаемость занятий, успеваемость. Вычислим коэффициенты корреляции t^ зависимой переменной Y – качество освоения блока математических дисциплин (КОБМД) (таб. 2) с переменными *1- *2..... *14- *15 , воспользовавшись корреляци онным и регрессионным анализом данных в пакете анализа программы Excel.

Таб.2. Коэффициенты корреляции 1^

Сопоставимый фактор	Переменная	Коэффициент корреляции
1. Исследовательское задание	*1	- 0,075
2.Опубликование статьи		0,157
3.Выступление на научной конференции	*3	0,213
4. Аудиторные контрольные работы (АКР)	*4	0,120
5. Домашние контрольные работы (ДКР)	*5	0,164
6. Работа над ошибками АКР	*6	- 0,161
7. Работа над ошибками ДКР	*7	- 0,060
8. Проведение коллоквиума	*5	- 0,319
9. Устный ответ студента с места		0,410
10. Работа студента у доски	*1D	0,196
11.Выступление с докладами на занятиях	*11	0,181
12. Проведение промежуточной аттестации	*i:	0,110
13.Формирование портфолио	*12	0,485
14. Посещаемость занятий	*14	0,340
15. Успеваемость	*15	0,468
Зависимая переменная Y – качество освоения блока математических дисциплин

Значения коэффициентов корреляции могут быть вычислены также по формуле 2 вручную:

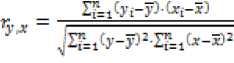
где X,у - средние значения переменных *6-Я , которые вычисляют по формулам 3 – 4.

* = ;S?=i*i,     (3)

y = ;^=ifi,     (4)

Отберем наиболее существенные из них четыре фактора *9- *13- *14- *1 , имеющих заметную корреляцию по шкале Чеддока 12 .

Значение коэффициента парной корреляции лежит в интервале от -1 до +1. В случае, когда коэффициенты положительны, это свидетельствует о прямой связи, т.е. когда растет одна переменная, то другая тоже увеличивается. Если отрицательная, то это говорит об обратной зависимости: одна растет, другая уменьшается. Почему же некоторые переменные дали знак корреляции «-» минус? Это говорит о том, что преподаватели высшей школы не достаточно серьезно относятся к работе над ошибками: считают, что исследовательское задание могут выполнять только неко- торые студенты, ну, а про коллоквиум было отмечено и ранее, что эта форма, к сожалению, не ис- пользуется преподавателями математики на современном этапе. Чем ближе значение коэффициента к 1, тем теснее связь. При равенстве нулю линейная связь полностью отсутствует.

Проверим выбранные четыре фактора на мультиколлинеарность. Вычислим для этого коэффициенты парной корреляции 1^ по форму- лам 1 – 3. В качестве критерия мультиколлинеарности примем соблюдение неравенств 5 – 7:

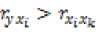
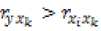
Если хотя бы одно из них не выполняется, то в модель включают тот фактор, который наиболее тесно связан с качеством обучения. Для проверки составим матрицу парной корреляции, используя отобранные ранее переменные (таб. 3).

Таб. 3. Корреляционная матрица

	Y	Xg	^12	Ху	X15
Y	1
9. Устный ответ студента с места -	0,410	1
13.Формирование портфолио - *13	0,485	0,273	1
14. Посещаемость занятий - ж14	0,417	0,600	0,462	1
15. Успеваемость - я15	0,468	0,230	0,286	0,417	1

Проверяя переменные Xg. Ху – устный ответ студента с места и посещаемость занятий, предварительно отобранные в модель, на мультиколлинеарность, получим: 0,410 > 0,600 (неверно); 0,417 > 0,600 (неверно); 0,600 <0,8 (верно). Видим, что первые два неравенства не выполняются. Следовательно, в модель включаем Хы – посещаемость занятий, фактор который наиболее тесно связан с качеством освоения образовательных программ, Xg – устный ответ с места исключаем из модели. Все остальные переменные удовлетворяют условиям 5 – 7, и следовательно, входят в модель. Таким образом, в модели остаются три переменные: х1а, x14, xu.

Линейная модель множественной регрессии в общем случае имеет вид:

ri = ao + or1-xil + - + an-x^ + Et         (8)

Используя технологию решения задач корре- ляционного и регрессионного анализа с помощью пакета анализа программы Excel (рис.2), получаем уравнение регрессии (9) для t = 3 трех независимых переменных, причем будет 14-1=3 + 1=4 коэффициентов регрессии (включая постоянную) (рис.2 столбец коэффициенты), отсюда число степеней свободы составит n - (k + 1) = 49 - 4 = 45 (рис. 2, пересечение столбца df и строки остаток).

Причем коэффициент множественной корреляции (индекс корреляции) равен R = 0,595 . Он отражает тесноту связи и точность модели. Коэффициент множественной корреляции, возведенный в квадрат, называется коэффициентом детерминации R1 = 0,354. Он показывает долю ва- под воздействием изучаемых факторов, т.е. определяет, какая доля качества обучения учтена в модели и обусловлена влиянием посещаемости, формирования портфолио и успеваемости. Стандартная ошибка оценки составляет 1,1 при выборке 49 респондентов. Для проверки значимости модели регрессии воспользуемся критерием Фишера, найдено F – значение, которое равно 8,2. Сравним его с табличным при доверительной вероятности 0,95. Если расчетное значение с vL = 3 и v2 = 45 степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой. Критическое значение критерия Фишера, определяемое по таблице Фишера-Снедекора, равно 2,8.

Т.к. ^Fpcc > 5na6, то уравнение регрессии можно признать адекватным. Это означает, что гипотеза о несоответствии заложенных в уравнении регрессии связей, реально существующим, отвергается.

Таким образом, полученное уравнение линейной модели влияния портфолио на качество освоения программ блока математических дисциплин является адекватным. Т.к. все коэффициенты при объясняющих переменных модели имеют знак «+», то будет повышаться результат освоения дисциплины от всех включенных в модель факторов. Из уравнения модели также следует, что существенное влияние на результирующую функцию оказывает фактор - формирование портфолио.

V = 3,324 + 0,015 ■ x13 + 0,223 ■ xL4 + 0,423 ■ x15, (9)

риации результативного признака, находящегося

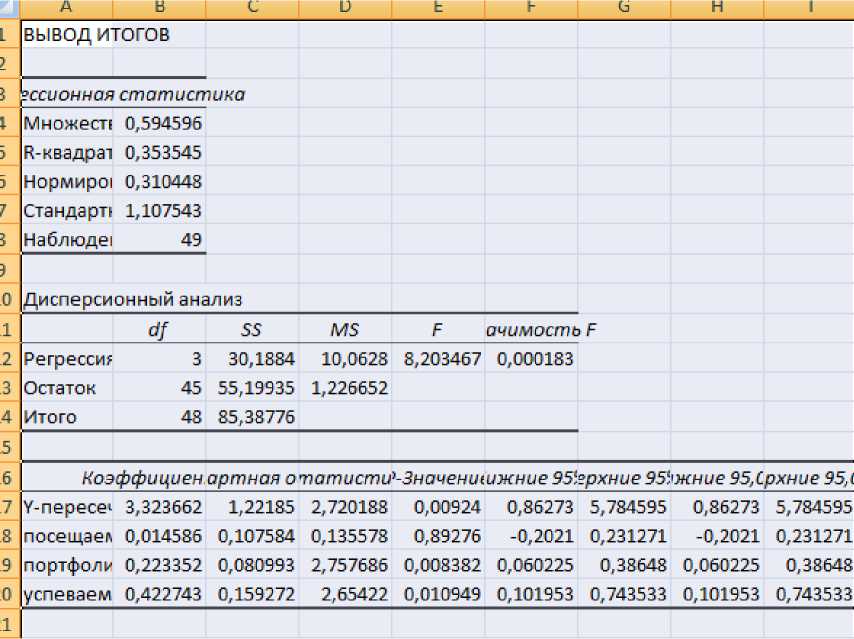
Рис. 2. Выводы по составлению уравнения линейной регрессии

INFLUENCE OF A PORTFOLIO ON THE QUALITY OF MASTERING MATHEMATICAL DISCIPLINES

1Samara State Aerospace University 2Samara State Technical University

The article carries out the construction of the linear multiple regression model based on the survey results of the teaching staff, which allows to evaluate the effect of pedagogical influence – the formation of the portfolio – on enhancing students' independent work and the quality of mastering the syllabus unit of mathematical disciplines Keywords: students, qualified teaching staff, questionnaires, portfolio, the correlation coefficient, multiple regression model.