Возможности компьютерного моделирования орбитальной эволюции космических объектов малой массы

В настоящий момент перспективным направлением исследования практически в любой области знаний является создание компьютерных технологий, расширяющих диапазон применяемых математических моделей исследуемых процессов и алгоритмов их эволюционного развития. Компьютерное моделирование процессов, которые трудно и просто невозможно воспроизвести в реальной жизни в целом ряде задач, является единственно возможным способом их исследования. Интенсивное развитие средств вычислительной техники способствовало расширению областей применения компьютерных технологий и их функциональных возможностей в исследовании эволюции сложных систем, к которым относятся динамические системы образования метеороидных комплексов из комет-родоначальниц. Исследования авторов статьи базируются на компьютерном моделировании процессов разрушения первоначальных объектов в эволюционном движении на протяжении всего их жизненного цикла.

Можно отметить три причины усиливающегося современного интереса к проблеме динамики небесных объектов:

– обеспечение безопасности жизни на Земле и необходимость изучения экстремальных явлений в атмосфере Земли, создаваемых в процессе движения космического объекта в атмосфере и выпадения остатков этого объекта на поверхность Земли;

– накопление значительного объема данных наблюдений за последние 50 лет о малых небесных объектах, требующего всестороннего анализа и осмысления;

– расширение сферы освоения космического пространства с практическими целями, которая предполагает обеспечение безопасности будущих протяженных космических миссий.

Проектирование рациональной компьютерной технологии обработки данных является довольно сложной задачей. Это обусловлено тем, что интерпретация относится к классу сложных многофакторных систем, когда учитываются как алгоритмы обработки, так и вопросы обмена данными между различными составляющими технологии, т.е. методы передачи данных в клиент-серверной системе, поскольку обобщенные характеристики обработки данных используются другими приложениями технологии для детализации показателей на других уровнях системы обработки данных. Одним из критериев оптимизации технологии является время реализации задачи на ЭВМ, зависящее как от аппаратной платформы, так и от методов обмена данными между приложениями в рамках конкретной операционной системы.

К настоящему моменту авторами разработана компьютерная технология, позволяющая моделировать процессы образования и дальнейшей эволюции метеороидных комплексов на значительных временных интервалах, основываясь на наблюдательных данных, с учетом условия неопределенности исходных параметров [1–2]. Технология–модульная.

Одним из ее достоинств является принцип открытости и наращиваемости – фундаментальный принцип проектирования современных операционных систем. Это позволяет наращивать функции технологии и при необходимости легко заменять или расширять список применяемых алгоритмов. Наличие имеющихся значительных объемов данных по малым телам Солнечной системы, как оказалось, недостаточно для построения исчерпывающих моделей эволюции небесно-механических систем. Процессы дезинтеграции оказывают существенное влияние на эволюцию движения самих малых тел, изменяя их орбиту, и формируют метеороидные комплексы, состоящие из выброшенных фрагментов различного размера и массы, движущихся по орбитам, сходным с первоначальной орбитой родительского тела.

В последние годы опубликовано довольно много сведений о целом ряде малых небесных тел, наблюдавшихся в течение длительных промежутков времени, что позволяет проводить вероятностное моделирование на основе более или менее достоверных (с точки зрения человеческого знания) начальных данных. Такая ситуация позволяет использовать компьютерную технологию как один из способов изучения населенности ближнего и дальнего космоса фрагментами распада родительских тел. Для обеспечения безопасности на Земле первейшая задача – выделение метеорных потоков из общей массы мете-ороидного вещества, вторгающегося в атмосферу, и определение тел, порождающих эти потоки (родительские тела). Отсюда, одной из главных задач анализа имеющихся данных наблюдений является их классификация.

Во второй половине XX века начинают разрабатываться вероятностные формы описания процесса эрупции вещества из родительского тела в любой точке траектории его движения и исследоваться модели существования возникающих при этом новых классов малых тел. Все чаще высказываются достаточно обоснованные предположения о том, что астероиды есть угасшие кометы, а количество наблюдаемых крупных тел во время действия метеорных потоков все увеличивается [3]. Вполне разумно принять кометы как основной источник создания астероидно-метеороидного комплекса в космическом пространстве.

По разработанной авторами компьютерной технологии [2; 4] могут быть выявлены основные тенденции изменений орбитальных элементов выброшенных фрагментов и построена общая картина заполнения региона космического пространства орбитами продуктов распада исследуемого объекта на расчетном интервале времени, что позволяет исследовать взаимосвязь комет с метеорными потоками, наблюдаемыми с Земли. В базовом варианте модели эрупции вещества из ядра кометы-родоначальницы рассматривается равновероятный выброс в заданном диапазоне угла разброса фрагментов в любой точке кометной орбиты с заданной скоростью выброса. Математический аппарат вероятностного моделирования орбитального кеплеровского движения фрагмента был опубликован [5–7]. В дальнейшем развитие алгоритма осуществлялось в сторону приближения модели к реальности. Были учтены гравитационные возмущения в форме двух составляющих: задачи N-тел и тесного сближения фрагмента с конкретной большой планетой Солнечной системы [8; 9]. Была рассмотрена возможность добавочного изменения орбитальных элементов за счет появления сублимационного процесса, возникающего при приближении кометы к Солнцу и создающего газовый поток, который выносит пылевую материю с поверхности кометы [10]. Следующим шагом усложнения модели явился учет влияния негравитационных эффектов, вызванных поглощением и последующим переизлучением солнечной радиации как кометой-родоначальницей [11], так вращающимся и невра-щающимся компонентами пылевой составляющей

______________________ Математическое моделирование физических, химических и биологических процессов                                35

метеороидного комплекса. Кроме того, принимается во внимание смещение родительского тела с основной орбиты как следствие выбросового эффекта [12].

Процессы, возникающие в недрах кометного ядра и на его поверхности, являются стохастическими, когда априори не известны начальные условия дезинтеграции и выброса твердой составляющей. А так как случайность есть неотъемлемая часть большинства природных явлений, то стохастический подход в данном случае оказывается весьма удобным. Поскольку стохастические модели порождают большие информационные массивы выходных данных, которые достаточно трудоемко анализировать обычными методами, необходимо создать представление результатов исследования в виде графиков и трехмерных изображений, автоматическую каталогизацию входных данных моделей, выходных данных моделирования и графических объектов. При этом визуальные образы результатов моделирования оказываются весьма полезными при концептуальном изучении поведения небесного объекта на больших временных интервалах. Кроме того, предполагается, что, поскольку в основном пользоваться данной технологией будут специалисты предметной области, должен быть создан простой, удобный и надежный интерфейс.

Компьютерная технология [2; 13] построена по принципу «клиент – сервер». Она является открытой, позволяет легко заменять отдельные модули и развивать систему, наращивая новые модули, без изменения структуры. Каждый модуль является приложением в среде Windows. В настоящий момент в состав технологии входят программный сервер и приложения, реализующие определенные задачи:

– моделирование и эволюция метеороидного комплекса;

– обработка результатов моделирования;

– выборка, анализ и построение графиков;

– трехмерная визуализация;

– автоматическое сохранение и просмотр входных и выходных данных, изображений и выходных 3D-графиков;

– визуализация сечения модельного роя плоскостью эклиптики;

– расчет предельных значений критериев, устанавливающих принадлежность фрагментов выброса конкретному метеороидному рою.

Математические алгоритмы, описания отдельных модулей, положения исследуемых объектов, их астрономические характеристики, ис- пользуемые при моделировании, вместе с полученными результатами и их анализом опубликовывались по мере разработки. Конкретные возможности технологии проиллюстрируем на примере исследуемых авторами небесных объектов, в качестве которых выбраны наиболее известные и долгонаблюдаемые кометы (табл. 1).

Таблица 1

Комета	Количество появлений	Годы появлений
1P/ Галлея (1909 R1)	26	1404 до н.э. – 1986 н.э.
21P/ Джакобини – Циннера	11	1910–1985 гг.
55P/ Темпеля – Туттля	10	1533–1899 гг.
26P/ Григга – Шьеллерупа	18	1907–1999 гг.
7P/ Понса – Виннеке	19	1819–1983 гг.

Первым результатом моделирования процесса дезинтеграции объекта получаются отклонения кеплеровских элементов орбиты выброшенных фрагментов от элементов орбиты родительского тела. Далее определяются непосредственно сами элементы орбит фрагментов, по которым строятся графики заполнения регионов космического пространства полученными орбитами. На всех рисунках ось ординат – значения величины истиной аномалии, которая соответствует точке дезинтеграции объекта, ось абсцисс – значения искомых величин. Орбита как кометы, так и фрагментов представлена шестью кеплеровскими элементами: а – большая полуось (а. е.), е – эксцентриситет, i – наклон орбиты (град.), ω – аргумент перигелия (град.), Ω – долгота восходящего узла (град.), Р – период обращения (год).

На рис. 1 в качестве примера представлен формат расчетных результатов для двух элементов орбиты (большая полуось и эксцентриситет) из шести возможных во всех известных их появлениях. Родительские тела имеют различные диапазоны начальных данных, а именно: скоростей выброса вещества, линейные и угловые параметры орбит, конкретные модели дезинтеграции и т.д.

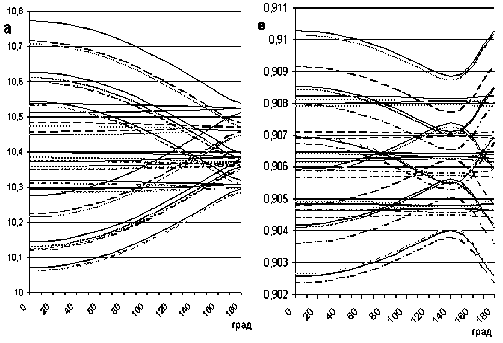
Рис. 1. Области вариаций большой полуоси (а.е.) и эксцентриситета орбит фрагментов выброса из ядра кометы Темпеля – Туттля II во всех появлениях со скоростями выброса до 25 мс-1

По полученным результатам можно провести 3D-визуализацию получаемого метеороид-ного комплекса для любого появления родительского тела. На рис. 2 приведены возможные комплексы, образованные кометой Галлея в появлениях 1404 г. до н.э., 1066, 1986 гг. н.э. и кометы Темпеля – Туттля II в появлениях 1533, 1733, 1899 гг. н.э.

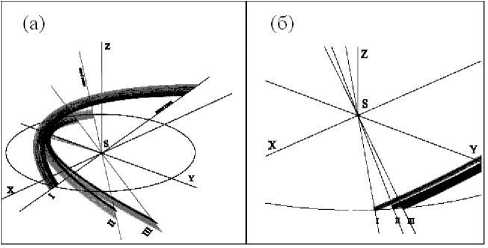
Рис. 2. Возможные метеороидные комплексы, порожденные: (а) – кометой Галлея в 1404 г. до н.э. (I), в 1666 (II) и 1986 гг. н.э. (III) и (б) – кометой Темпеля – Туттля II в 1533 (I), 1733 (II), 1899 гг. н.э. (III) в районе орбиты Земли

Показан возможный регион космического пространства, в котором может располагаться весь комплекс, возникший за счет регулярных выбросовых явлений в комете за весь ее жизненный цикл. Рассмотрение метеороидного комплекса с детализацией положения точек выброса на орбите и диапазона скоростей выброса позволяет уточнить структуру получаемого комплекса (рис. 3).

Учитываемые в технологии гравитационные возмущения включают две основные составляющие:

N-тел, определяемые численным интегрированием с применением алгоритма Э. Эверхарта, для N ≥ 2;

– возмущения от гравитационного потенциала большой планеты при сближении с нею малых тел. Используются аналитические формулы промежуточной некеплеровской гиперболической орбиты, основанной на симметричном варианте обобщенной задачи двух неподвижных центров и учитывающей сжатие центрального тела, за которое принимается планета сближе- ния.

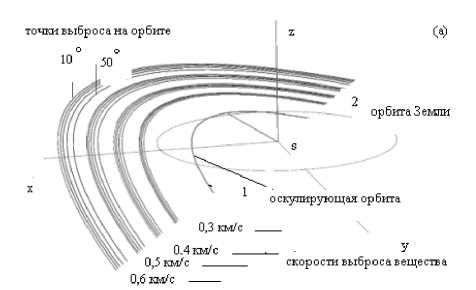
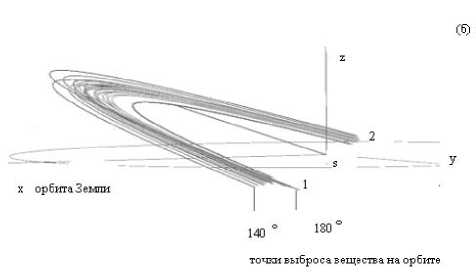
Рис. 3. Часть возможного метеороидного комплекса кометы Галлея над эклиптикой, иллюстрирующая его слоистую структуру для разного расположения точек выброса вещества и разных скоростей выброса:

а – вблизи перигелия; б – в районе афелия.

Результаты расчетов вариаций параметров орбит небесных объектов в различные даты появлений и соответствующих им моделируемых комплексов могут быть получены в табличном и графическом видах. На рис. 4 как пример приведены вариации двух параметров метеороидного комплекса кометы Темпеля – Туттля II в появлении 1600 г. Каждая кривая графика представляет вариации одного параметра при учете влияния различного количества планет.

Кроме графиков может быть получена 3D-визуализация состояния Солнечной системы на момент проведения расчетов (рис. 5).

– гравитационные возмущения в задаче

______________________ Математическое моделирование физических, химических

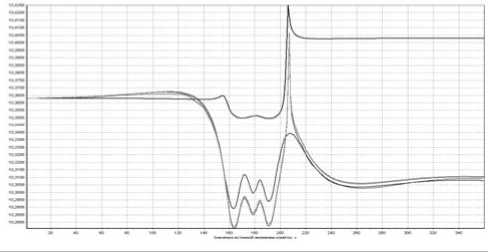
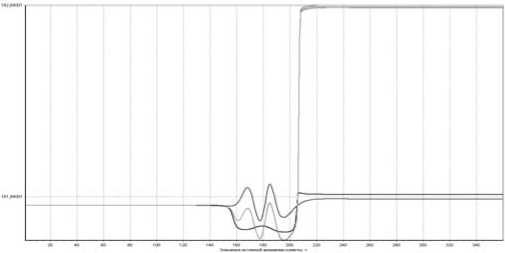
Рис. 4. Вариация большой полуоси (вверху) и угла наклона (внизу) метеороидного комплекса кометы Темпеля – Тутт-ля II (1600 г.) в зависимости от учета гравитационных возмущений различного состава планет

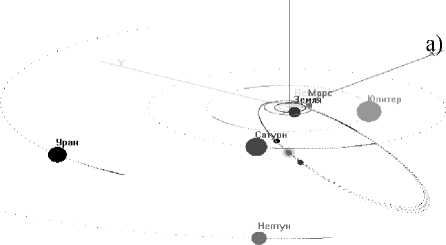
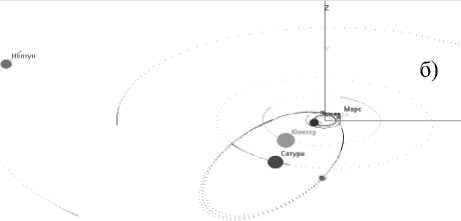
Рис. 5. Трехмерная модель расположения небесных тел в пространстве при моделировании метеороидного комплекса кометы Темпеля – Туттля (1600 г.). Комета находится в точке с истинной аномалией: а – 150°; б – 203°.

Дисперсия орбит выброшенных фрагментов, возникающая из-за первоначального разброса скоростей, со временем увеличивается из-за сближения метеороидных тел с более крупны-

ми небесными объектами. Метеорный поток, наблюдаемый на Земле, может быть определен в терминах гелиоцентрических или геоцентрических параметров. Однако при любом определении критерием установления принадлежности метеороидных тел конкретному метеорному потоку является мера близости орбит. Попытки разработать универсальный метод для установления такой принадлежности пока еще малорезультативны [14–18 и др.].

В рамках исследования принадлежности отдельного объекта к совокупности метеороидных тел может быть поставлена следующая задача: выяснить, каковы пределы значений критериев общности и их временная и пространственная эволюция для фрагментов, образующих метео-роидные комплексы при дезинтеграции конкретных родительских тел. Следует заметить, что все еще не имеется достаточно точного и уверенного метода обработки наблюдательных данных, исключающего как неточности наблюдения, погрешности приборов, так и несовершенство алгоритмов обработки. Для успешного решения, по-видимому, следует двигаться с двух противоположных сторон. В этих условиях наличие модельного метеороидного комплекса с его характеристиками может явиться основой, на которую имеет смысл накладывать наблюдательные данные для уточнения или определения генетической связи рассматриваемых объектов.

Применяющиеся критерии общности можно подразделить на три весьма условных класса (табл. 2).

Таблица 2

Класс	Основание
критерий Саутуорта – Хоккинса критерий Драммонда критерий Йопека	гелиоцентрические координаты
геокритерий	геоцентрические координаты
динамический критерий	воздействие возмущающей силы

Поскольку в нашем случае критерии рассчитываются по орбитам моделируемых фрагментов выброса, мы изначально знаем их родство. Полученные по орбитальным элементам фрагментов выброса с максимальным удалением от кометы-родоначальницы числовые значения любого из критериев могут быть приняты за пороговые. На рис. 6 приведены результаты, соответствующие вычислениям для метеороидного ком- плекса кометы Понса – Виннеке в 4-х появлениях (а – 1819 г., б – 1886 г., в – 1921 г., г – 1983 г.) при скорости выброса фрагментов 50 м/с. Видно, что, во-первых, кривые вариаций критериев в рассчитываемых случаях расположены неодинаково; во-вторых, для данного метеороид-ного комплекса максимальные значения дает геокритерий, минимальные – критерий Йопека; в-третьих, картина расположения кривых вариаций критериев общности в ретроспективе от 1819 г. до 1983 г. весьма изменчива. Так, для ме-теороидного комплекса 1819 г. кривые критериев весьма переплетены друг с другом, для 1886 г. картина более спокойная, в 1921 г. уже все кривые отделены друг от друга, а в 1983 г. всё стабильно. В-четвертых, числовые пороговые значения для первых трех случаев крайне малы, но все – в пределах одной разрядной сетки, в чет- гии можно показать для короткопериодической кометы 17Р/Холмса, сильнейшее явление вспышечной активности которой было зарегистрировано в октябре 2007 года.

Комета 17Р/Холмса была открыта 6 ноября 1892 г. Считается, что она была открыта в момент мощной вспышки. Период обращения кометы составляет 7 лет. Она наблюдалась в десяти возвращениях из семнадцати возможных. После 1906 года комета была утеряна и до 1964 года вообще не наблюдалась. С 1964 г. регулярно наблюдалась как объект малой яркости, в 2000 году яркость объекта увеличилась. Последний раз она прошла перигелий 4 мая 2007 г. с той же яркостью, но 24 октября 2007 г. увеличила блеск за сутки, по разным оценкам, от 400000 до 1000000 раз.

Таблица 3

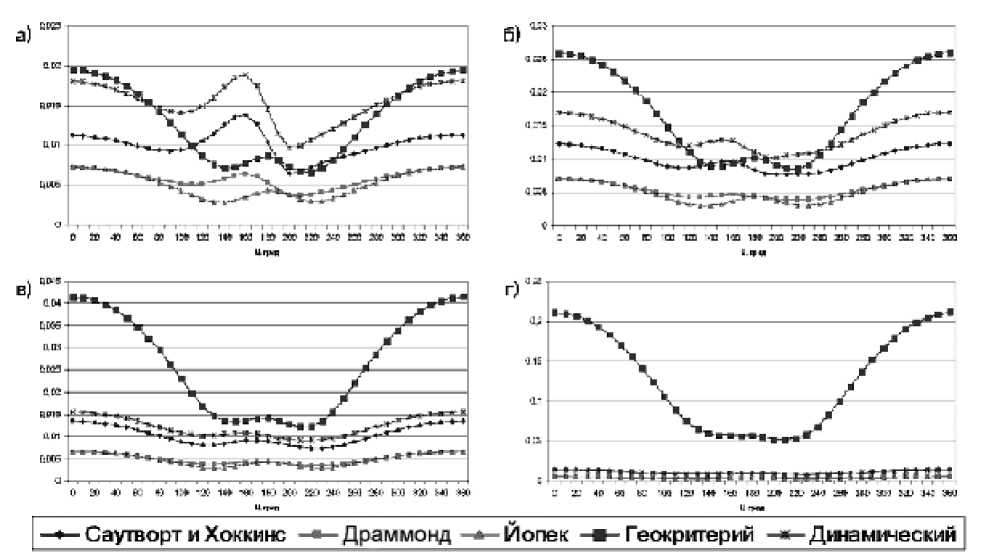
Рис. 6. Вариации значений различных критериев общности для кометы Понса – Виннеке

вертом случае числовые значения увеличились на порядок. Следует отметить, что для каждой рассматриваемой кометы интерпретация полученных численных и графических материалов индивидуальна [19–20].

Интересным результатом проводимой работы является возможность определения для изучаемого малого тела областей, оказавшихся недоступными для наземных наблюдений, и дальнейшее восстановление полной траектории существования в пространстве и времени этого объекта. Этот аспект применения техноло-

Элементы орбит кометы Холмса по данным моделирования

______________________ Математическое моделирование физических, химических

№	Дата	а (а.е.)	e	P(год)	to (град)	Q (град)	(град)
1.	15.06.1892	3,625	0,4095	6,9018	14,28	333,22	20,805
2.	09.04.1899	3,615	0,4113	6,8732	14,06	333,14	20,814
3.	16.03.1906	3,609	0,4123	6,8561	14,26	333,08	20,826
4.	21.07.1913	3,778	0,3798	7,3433	22,08	330,72	19,520
5.	30.11.1920	3,788	0,3786	7,3725	22,189	330,66	19,498
6.	09.04.1928	3,783	0,3802	7,3579	22,084	330,66	19,508
7.	01.08.1935	3,764	0,3843	7,3025	21,892	330,49	19,528
8.	24.11.1942	3,762	0,3843	7,2967	22,141	330,40	19,524

9.	19.03.1950	3,782	0,3798	7,3550	21,997	330,24	19,472
10.	28.07.1957	3,790	0,3778	7,3783	21,959	330,21	19,442
11.	09.12.1964	3,779	0,3796	7,3462	22,075	330,18	19,463
12.	21.02.1972	3,670	0,418	7,0307	23,88	327,79	19,050
13.	10.03.1979	3,675	0,417	7,0451	24,048	327,72	19,036
14.	24.03.1986	3,681	0,416	7,0623	23,80	327,68	19,027
15.	15.04.1993	3,686	0,414	7,0767	23,69	327,67	18,997
16.	14.05.2000	3,677	0,416	7,0508	23,81	327,64	19,01
17.	04.05.2007	3,615	0,435	6,8732	24,65	326,57	18,95

Была осуществлена модельная дезинтеграция кометы по всей ее орбите со скоростями выброса до 100 м/с для всех (наблюдавшихся и незарегистрированных) появлений. Результирующая информация может быть представлена исследователю как в форме расчетной таблицы, так и в форме рисунка [21]. Сравнение результатов моделирования (табл. 3, светлые строки) с данными наблюдений показали вполне удовлетворительное согласие. Используя полученные элементы орбит кометы, авторы провели моделирование дезинтеграции ядра кометы для всех 17 обращений и получили возможный метеоро-идный комплекс кометы 17/Р Холмса.

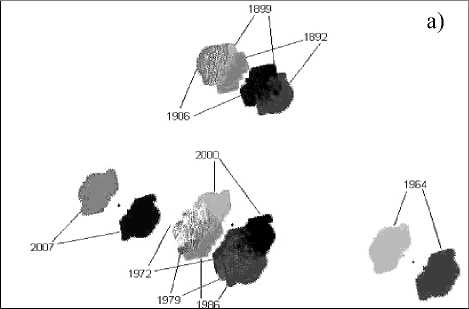
Рис. 7. Расположение областей пересечения орбит фрагментов выброса из ядра кометы с плоскостью эклиптики: (а) метеороидные комплексы, полученные по исходным данным наблюдений; (б) метеороидные комплексы, полученные по исходным данным моделирования

На рис. 7 представлена проекция эволюционного развития этого метеороидного комплекса на плоскость эклиптики. Правая часть рисунка 7а – это картина расположения в пространстве и временная эволюция метеороид-ного комплекса, полученного с использованием в качестве исходных данных для моделирования наблюдённых элементов орбиты кометы в соответствующий год её появления. Поскольку в процессе моделирования получаются отклонения орбитальных элементов выброшенных фрагментов в пределах ±δf (где f – элементы орбиты а, е, i, Ω, ω), то комплекс имеет две ветви по отношению к орбите родительского тела для каждого обращения кометы. На рис. 7б слева мы имеем аналогичную картину, полученную для всех 17 обращений кометы с исходными данными табл. 3. Четко выделяются три области концентрации комплекса (рис. 7а), ограниченные временными интервалами наблюдения кометы: 1892–1906 гг. (область I), 1964 г. (область II), 1972–2007 гг. (область III). Перемещение в пространстве комплекса происходит от области I к области III. Восстановленные моделированием орбиты ненаблюдавшихся обращений кометы со своими комплексами группируются в области II. Внимательное рассмотрение временных интервалов позволяет предположить, что комета находится в конкретной области пространства на протяжении восьми обращений, после чего перемещается в другой регион. Если это соответствует действительности, то комету открыли в момент вспышки, после которой через два обращения она резко изменила свою орбиту. Все восемь последующих обращений (1913–1964 гг.), кроме последнего (1964 г.), были с Земли ненаблюдаемы или не идентифицировались с кометой Холмса. В следующей группе наблюдений (область III) в настоящий момент имеется 6 наблюдений, и, возможно, в этой области комета появится еще дважды. Не останавливаясь на детальной астрономической интерпретации получаемых результатов, общая картина заполнения космического региона фрагментами моделирования изучаемых объектов приведена на рис. 8.

Полагаем, что приведенные иллюстрации дают представление, насколько глубоко проникновение компьютерных технологий в столь сложную, труднодоступную для изучения и необходимую человеку область, связанную с освоением космического пространства.

Наличие современных вычислительных средств и их перспективное развитие требует разработки новых способов проведения исследований, особенно в областях, трудно реализу- емых экспериментально. Одним из таких способов, по мнению авторов данной работы, являются компьютерные технологии моделирования изучаемых процессов или явлений.

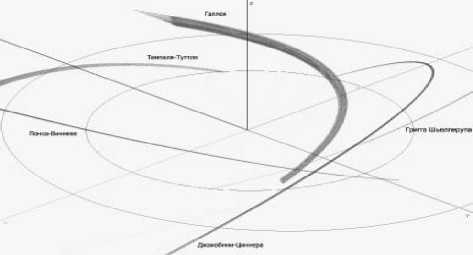
Рис. 8. Возможная метеороидная обстановка, формируемая пятью кометами (Галлея, Григга – Шьеллерупа, Джакоби-ни – Циннера, Понса – Виннеке, Темпеля –Туттля II) в районе между Землей и Марсом (вид над плоскостью эклиптики)