Аппроксимация зависимости относительного количества пожаров в Российской Федерации от возраста виновника пожара

*

К данному времени нет исследований по математической аппроксимации имеющихся данных [1] о зависимости количества пожаров на 10000 человек возрастной группы в Российской Федерации от возраста виновника пожара. Основная трудность проведения исследования состоит в том, что данных для различных конкретных значений возраста виновника пожара в статическом сборнике [1] нет. Однако есть данные по количеству пожаров на 10000 человек возрастной группы для возраста виновника, попадающего в каждый из 7 интервалов возраста виновника (Таб. 1).

* *

Исследовать данные, сгруппированные по интервалам, неудобно. Самый простой подход к решению задачи состоит в введении ранговой переменной Х. Эту переменную (совпадающую с номером возрастного интервала) мы используем для идентификации интервала возраста виновника пожара

Например, Х = 1 задает возраст виновника в интервале от 0 до 6 лет, Х = 2 диапазон от 7 до 13 лет, Х = 3 интервал от 14 до 15 лет, Х = 4 диапазон от 16 до 19 лет, Х = 5 от 20 до 40 лет, Х = 6 диапазон от 41 до 59 лет, Х = 7 больше 60 лет.

Таблица 1

Количество пожаров на 10000 человек возрастной группы в РФ по возрасту виновника

Х	Возраст виновника	2015	2016	2017	2018
1	0-6	0,69	0,54	0,44	0,41
2	7-13	0,98	0,91	0,85	0,82
3	14-15	0,65	0,47	0,49	0,53
4	16-19	0,66	0,61	0,62	0,56
5	20-40	3,4	3,08	2,85	2,76
6	41-59	6,05	5,66	5,22	5,2
7	>60	4,31	4,2	4,13	4,1

Приведенные возрастные интервалы не равномерны, имеют различные временные продолжительности. Однако именно эти интервалы возраста виновника пожара приведены в сборнике [1]. Поэтому вынуждены использовать их.

Зависимость относительного количества погибших при пожарах в России от возраста виновника пожара (Рис. 1) нелинейна.

Отметим, что полученный график (Рис.1) походит накривую роста популяции в биологии.

Поэтому рассмотрим возможность применения закона роста биологической популяции для аппроксимации зависимости количества пожаров на 10000 человек возрастной группы от возраста виновника пожара.

Модель Ферхюльста

Количество особей P(t) в популяции описывается функцией Ферхюльста [2]:

1 P(t)=^fe.G = exp(rt)        (1)

(

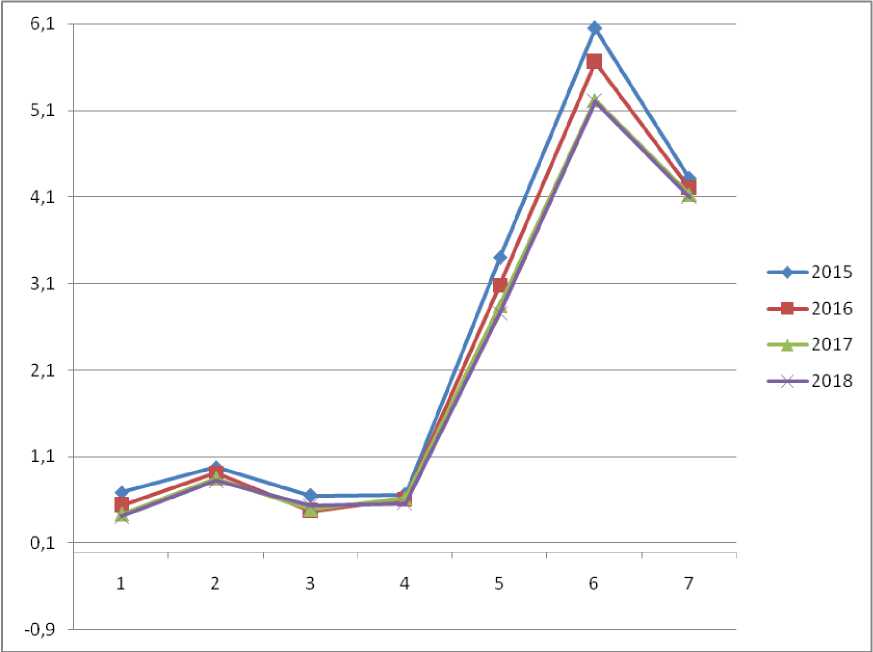
Рис. 1. Количество пожаров на 10000 человек возрастной группы в России по возрасту виновника пожара

где Р0 - начальная численность популяции, К - емкость среды (максимальная численность популяции), r - скорость размножения.

При аппроксимации относительного количества погибших при пожарах смысл констант в уравнении (8) меняется. Так Р0 -минимальное относительное количество погибших при пожарах. Полагаем Р0 = 0,01. Если положить Р0 = 0, то и все остальные значения Р(t) = 0, а этого не наблюдается. Далее К - максимальное количество пожаров на 10000 человек возрастной группы. Можно ожидать, что К равно или больше максимального из имеющихся фактических значений (Таб. 1). Параметр r - скорость изменения количества пожаров на 10000 человек возрастной группы. Параметры К и r будут определены подбором. По результату подбора для количества пожаров будем использовать аппроксимацию

^Ym = „ ^.v ⁰ ^^eXP (^rX) (2) ^м K+P_O(G-1) ⁷

Оптимальные значения параметров К и r находили с помощью средства Поиск решения программы Microsoft Excel. Они должны давать минимум среднего значения квадрата ошибки. Под ошибкой понимаем величину е = Yм -Y, где Yм - модельное значение, а Y - фактическое значение.

Минимум был обнаружен при значениях параметров К = 6,227922 и r =1,338879,. Р0 = 0,01. Среднее значение ошибки для 2015 составило 0,02, а среднее значение квадрата ошибки 0,76 (Таб. 2).

Коэффициент линейной корреляции Пирсона между модельными и фактическими значениями равен R = 0,92. Квадрат этого значения дает величину коэффициента детерминации R2 = 0,8537. Это означает

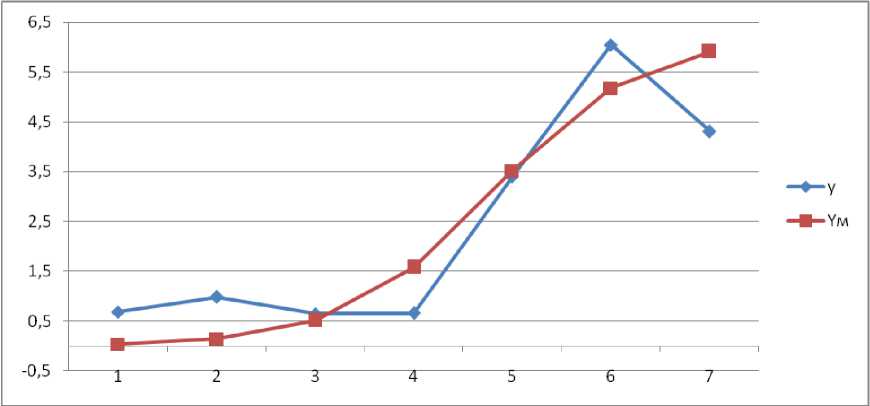
Рис. 2. Сравнение фактических значений (Y) с результатами модели Ферхюльста (Yм) для 2015 года

Таблица 2

Модель Ферхюльста для 2015 года

Х Y Yм e e2 1 0,69 0,04 -0,65 0,43 2 0,98 0,14 -0,84 0,70 3 0,65 0,51 -0,14 0,02 4 0,66 1,58 0,92 0,85 5 3,4 3,52 0,12 0,01 6 6,05 5,18 -0,87 0,75 7 4,31 5,92 1,61 2,58 среднее 0,02 0,76 что модель Ферхюльста объясняет 85,37% фактических значений.

Сравнение графиков фактических имодель-ных количеств пожаров на 10000 человек возрастной группы в России показало, что модель Ферхюльста дает достоверное описание ситуации только для возраста виновника пожара в диапазоне 20-40 лет (Рис. 2).

Результаты для 2016 - 2017 годов аналогичны, отличаются только значениями констант К, Р0, r (Таб. 3).

Отметим, что модель Ферхюльста дает довольно большое значение коэффициента детерминации. Оно находится в диапазоне 85,37 - 89,45 %.

Заметные отличия модельных значений от фактических требуют корректировки модели.

Модель Ферхюльста с переменной скоростью роста

Попробуем использовать аппроксимацию

^d^'0"^^ (3)

Величина a(X) имеет смысл ускорения. Допустим, что ускорение постоянно на каждом из возрастных интервалов.

Абсолютно точное воспроизведение фактических показателей (Таб. 4) происходит при константах К =6,227922, Р0 = 0,01 и ускорении, задаваемого константами на каждом возрастном интервале (Таб. 5).

Таблица 3

Константы модели Ферхюльста

Год	K	P 0	r	R2
2016	5,854492	0,01	1,314668	87,02%
2017	5,4596	0,01	1,30212	89,45%
2018	5,3	0,01	1,337865	88,66%

Таблица 4

Модель Ферхюльста с переменной скоростью роста для 2015 года

Х	Y	Yм	e
1	0,69	0,69	0
2	0,98	0,98	0
3	0,65	0,65	0
4	0,66	0,66	0
5	3,4	3,4	0
6	6,05	6,05	0
7	4,31	4,31	0

Таблица 5

Ускорение для различных возрастных интервалов для 2015 года

X	а
1	4,349923
2	0,404648
3	-0,47156
4	0,017062
5	2,316771
6	3,342234
7	-2,71677

В этом случае ошибка модели равна нулю.

Результаты для 2016 - 2017 годов аналогичны, отличаются только значениями констант K, Po, а1, а2 , а3, а4, а5, а6, а7 (Таб. 12). 2

Таким образом абсолютно точное описание зависимости количества пожаров на 10000 человек возрастной группы в Российской Федерации от возраста виновника по- жара дает модель Ферхюльста с переменной скоростью роста. При этом ускорение роста в каждом возрастном интервале считали постоянной величиной.

Таким образом, представления биологии о росте популяции оказались продуктивными при поиске аппроксимации зависимости количества пожаров на 10000 человек в Российской Федерации от возраста виновника пожара.

Таблица 12

Год	K	P 0	а 1	а 2	а 3	а 4	а 5
2016	5,854492	0,01	4,084046	0,594039	-0,74596	0,287071	2,255937
2017	5,4596	0,01	3,866382	0,743671	-0,62603	0,261821	2,14299
2018	5,3	0,01	3,792198	0,780716	-0,49915	0,061369	2,218922

Год	а 6	а 7
2016	3,266324	-2,4392
2017	2,993159	-1,94788
2018	3,868177	-2,72258

Константы модели Ферхюльста с переменной скоростью роста