Исследование растворимости лактозы в присутствии глюкозы и сахарозы

Современные продукты питания должны удовлетворять множеству требований, предъявляемых к их качеству и составу. Одним из этих критериев является пониженная калорийность. В этой связи нами разработан сгущенный молочный продукт с частичной заменой сахара на крахмальную патоку [1]. Патока представляет собой смесь углеводов различной молекулярной массы, большая доля которых приходится на глюкозу [2]. В рамках нашего исследования значительный интерес представляет исследование влияния сахарозы и глюкозы на растворимость лактозы, поскольку растворимость влияет на кристаллизацию лактозы, а, следовательно, и на показатели качества готового продукта.

В качестве подготовительного этапа исследований выступает планирование эксперимента, целью которого является исследование влияния на процесс нескольких факторов и получение математической модели процесса с учетом взаимовлияния на него всех принятых к исследованию факторов [3]. Нами был выбран полный двухфакторный эксперимент, так как число факторов, влияющих на растворимость лактозы равно двум – это температура и концентрация примесей.

N = Lk, где N – число опытов при ПФЭ;

L – число уровней;

k – количество факторов.

Число опытов соответствует числу сочетаний из n элементов при их изменении на двух уровнях. В нашем случае матрица будет иметь вид N=22.

Температура и концентрация были выбраны на основании литературных данных. Температура является наиболее важным параметром в процессе растворения лактозы, значения температур выбраны исходя из технологического процесса кристаллизации лактозы [2]. Температура 35 °С соответствует стадии усиленной кристаллизации лактозы при производстве сгущенных молочных консервов, а температура 20 °С является конечной точкой процесса охлаждения. Таким образом, эти значения температур являются наиболее значимыми при производстве сгущенного молока с сахаром, чем и обуславливают их выбор в качестве входного параметра.

Концентрация примесей углеводов так же является важным фактором в разрабатываемой нами технологии. Предлагается заменить порядка 20–40 % сахарозы на крахмальную патоку, этим и обусловлен выбор именно таких концентраций примесей.

Таблица 1. Таблица значений уровней и интервалов варьирования на основе предварительной информации в натуральной размерности

Фактор	Уровни варьирования			Интервал варьирования, Δ
	-1	0	+1
Температура,t °С	20	27,5	35	7,5
Концентрация примесей, Hпр кг/кгводы	0,24	0,32	0,48	0,12

Найдем числовые значения верхнего и нижнего уровней факторов в безразмерном выражении и составим по ним план ПФЭ (табл. 2).

Таблица 2. План ПФЭ в безразмерном выражении факторов

№ опыта        Х1             Х2             Х12             У

1	+1	+1	+1	У1
2	-1	+1	-1	У2
3	+1	-1	-1	У3
4	-1	-1	+1	У4

Далее на основании плана ПФЭ в безразмерном выражении (табл. 2) составляем рабочую матрицу в натуральной размерности (табл. 3), для чего осуществляем перевод величины фактора в натуральную размерность, и проводим эксперимент согласно методике [4]. Результаты по растворимости лактозы Нл и рабочая матрица планирования эксперимента представлены в таблице 3.

Таблица 3. Рабочая матрица планирования эксперимента в натуральной размерности

№	Температура t, ° C	Концентрация примесей, Нпр, кг/ кгводы	Растворимость лактозы, Нл, кг/кгводы
			y1	y2	y3	0
1	35	0,48	0,261	0,261	0,258	0,260
2	20	0,48	0,155	0,153	0,151	0,153
3	35	0,24	0,305	0,310	0,309	0,308
4	20	0,24	0,174	0,174	0,172	0,173

Для оценки воспроизводимости полученных данных о растворимости лактозы было определено среднее значение для трех повторных опытов, отклонение от среднего (yi - ), квадрат отклонения (yi - )2 , квадрат среднеквадратичного отклонения δ S2n и среднеквадратичное отклонение δ Sn. Результаты представлены в таблице.

Таблица 4. Данные для оценки воспроизводимости результатов по растворимости лактозы.

№	Температура, t, °C	Концентрация примесей, Нпр, кг/ кгводы	yi	0	yi -	(yi -0) 2	δ S 2n	δ S n
1	35	0,48	0,261	0,260	0,001	0,000001	0,000003	0,001732
			0,261		-0,001	0,000001
			0,258		-0,002	0,000004
2	20	0,48	0,155	0,153	0,002	0,000004	0,000004	0,002000
			0,153		0,000	0,000000
			0,151		-0,002	0,000004
3	35	0,24	0,305	0,308	-0,003	0,000009	0,000007	0,002646
			0,310		0,002	0,000004
			0,309		0,001	0,000001
4	20	0,24	0,174	0,173	0,001	0,000001	0,0000015	0,001225
			0,174		0,001	0,000001
			0,172		-0,01	0,000001

Для определения достоверности повторных опытов был использован критерий

Стьюдента,

Lpac4         — LTa6ji где среднеквадратичное отклонение:

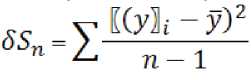
где n – число повторных опытов.

Например, для первого опыта определяем:

Для трех повторностей (n=3) и доверительного интервала α=0,95 ^тябл =4,30 [3].

Таким образом, неравенство выполняется, следовательно, результаты повторных опытов не являются ошибочными. Аналогично проведены проверки для всех остальных опытов. Для максимального и минимального значений растворимости (у) расчетное значение критерия Стьюдента представлено в таблице 5.

Номер опыта

Для максимального значения

Для минимального значения

Таблица 5. Расчетные значения критерия Стьюдента для максимального и минимального значений растворимости (у).

1	0,577	-0,577
2	1,000	-1,000
3	0,756	-1,134
4	0,816	-0,816

Далее полученные значения критерия Стьюдента сравниваем с табличным значением и по соотношению этих значений делаем вывод об ошибочности / безошибочности опытов. Табличное значение составляет 4,30 (для α=0,95; u=3). Сравнивая расчетные значения с табличным делаем вывод о том, что все опыты не являются ошибочными, так как все полученные значения меньше табличного.

Проверку однородности дисперсий осуществляют по критериям Фишера и Кохрана.

Критерий Фишера рассчитывают по формуле:

г =------- ss2 .

n mm ;

0,00000?

F =_______

0,0000015

= 4,667

.

Полученное расчетное значение сравнивают с табличным, который определяют при α=0,95 и степенях свободы f1= f2= n-1=2,  =19 следовательно диспер сия однородна.

Критерий Кохрана рассчитывают по формуле:

~ max

;

0,000007

G =_______

;

0,000011s

= 0,608?

^тайл =0,64 при α=0,95 и степенях свободы f1=n-1=2 и f2=N=4 [5]. Посколь- ку , следовательно условие выполняется.

По результатам ПФЭ составлена математическая модель объекта исследования, представленная в виде полинома первой степени, в котором помимо линейных членов есть член, учитывающий эффект парного межфакторного взаимодействия:

у = a_n + сц х₁ + а₂х₂ + а₁₂х₁ х₂

где а0, а1, а2, а12 – коэффициенты.

Коэффициенты рассчитывались по уравнениям и составили:

n _У1+У2+У3+У4 Q _ У1-У2+У3-У4 1              4            ; a _ У1+У2-У3-У4 2              4            ; п _У1-у2-у3+У4 12           4

0,260 + 0,153 +0,308 + 0,17з n ■ "--            A            "0,224. ;; 0,260 - 0,153 + 0,308 - 0,173 n сц = — ---------------------------= 0,06i 1                            4                                        ; 0,260 + 0,153 - 0,308 - 0,17з n <2, - —---------------------------=-0,01? . 2                            4                                           ; 0,260 - 0,153 - 0,280 + 0,17з n clA2= — ---------------------------= -0,007 ; ;.

Путем подстановки полученных коэффициентов получаем математическую модель объекта исследования вида:

y= 0,224+0,061x1- 0,017x2–0,007x12.

На основании полученной математической модели можно сделать вывод, что на растворимость оказывают влияние как температура (х1), так и концентрация примесей (х2). Причем температура повышает растворимость, о чем свидетельствует положительный коэффициент перед ней, а концентрация примесей наоборот, способствует снижению. Совместное влияние температуры и концентрации примесей незначительно.

Для подтверждения адекватности и работоспособности полученной модели необходимо определить границы доверительных интервалов в уравнении модели.

Определяем границы доверительного интервала для коэффициентов регрессии при α=0,95 с учетом значения дисперсности воспроизводимости:

где 6S_a – дисперсия воспроизводимости.

Определяем дисперсность воспроизводимости для серии измерений (N=4):

X6S^

N '

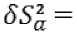
где

55^ - отдельный опыт; ^^ - серия опытов.

0,000003 + 0,000004 + 0,000007 + 0,000001s

8S^ = --------------------------------------- =0,000002875,

4,30 х VO,00000287s

5^ = ±---------------- -= 0,003646

Все коэффициенты в математической модели значимы, так как они превышают границы доверительного интервала.

Далее необходимо вычислить расчетные значения растворимости (у) и величину относительной погрешности.

Для расчета теоретических значений использовали полученную математическую модель объекта исследования и рабочую матрицу (таблица 3).

На основании проведенного полного двухфакторного планирования эксперимента выбраны условия для проведения опытов. В ходе эксперимента получены опытные значения растворимости (таблица 6).

Таблица 6. Опытные и расчетные значения растворимости

№	Опытное значение	Расчетное значение	Абсолютная погрешность	Относительная погрешность,%
1	0,260	0,261	0,001	0,385
2	0,153	0,153	0	0
3	0,308	0,309	0,001	0,325
4	0,173	0,173	0	0

Сравнивая расчетные значения растворимости со значениями, полученными опытным путем, можно заключить, что расхождение между ними крайне не значительное, что свидетельствует о целесообразности использования планирования эксперимента в качестве подготовительного этапа исследований.