Компьютерное геометрическое конструирование заданий занимательного характера как средство развития пространственного воображения обучающихся основной школы на уроках математики

В условиях массовой информатизации общества и образования все более востребованными становятся специалисты с высоким уровнем интеллекта. Одним из важнейших составляющих интеллекта является пространственное воображение, а его развитие становится крайне важным условием успешности обучения в школе. Пространственное воображение оказывает существенное влияние на изучение целого ряда дисциплин, лидирующую позицию среди которых, по нашему мнению, занимает математика. Имея хорошо развитые пространственные представления, обучающимся значительно проще представить абстрактные математические понятия и объекты, наполнить их конкретным содержанием.

В разное время вопросами развития пространственного воображения занимались такие исследователи, как А.Н. Леонтьев, А.А. Смирнов, Г.И. Лернер, Ж. Пиаже, И.С. Якиманская и целый ряд других ученых. Большинство практикующих педагогов и психологов отмечают, что формировать и развивать пространственное воображение следует уже в младших классах. Именно в этом возрасте учебный процесс базируется на живом созерцании, в котором большую роль играет уровень развития когнитивных функций: внимания, памяти, восприятия, наблюдения, мышления и воображения, в том числе пространственного.

Формирование пространственного воображения должно быть реализовано непосредственно в ходе современного образовательного процесса, оно способствует освоению основного геометрического материала школьных курсов, в частности таких разделов, как стереометрия, где обучающиеся учатся читать изображения основных геоме-

трических фигур, также обучаются навыкам представления требуемого предмета и умениям оперировать сразу несколькими геометрическими объектами.

На сегодняшний день наблюдается четкое снижение математической подготовленности обучающихся, что проявляется в первую очередь в низком уровне сформирован-ности пространственного воображения. Это обусловлено в том числе и тем, что школьный курс математики изучается в основном с использованием традиционных методов обучения, многие преподаватели редко используют информационные технологии, которые могли бы значительно облегчить процесс обучения, сделать его более интересным и понятным. На сегодняшний день для обучения математике разработано более 50 программ, таких, например, как Живая математика и GeoGebra, позволяющих создавать динамические чертежи с использованием компьютерной анимации. Следуя [3], под компьютерной анимацией мы будем понимать компьютерную имитацию реального или идеального процесса с помощью изменения формы объектов, текста или показа последовательных изображений с фазами движения.

В настоящей статье мы остановимся на возможностях интерактивной математической системы «Живая математика» [1]. Не вдаваясь в подробности и детали, опишем процедуру конструирования в этой среде обучающимися 7–9 классов под руководством учителя математики динамических чертежей для заданий занимательного характера, направленных на развитие пространственного воображения. К целевой аудитории, которой предназначены эти задания, в первую очередь мы относим всех тех обучающихся, кто участвует в разработке этих заданий, и, конечно, тех, кто будет эти задания выполнять. Как показал наш опыт, таковыми являются ученики не только основной школы, но и выпускных классов. Нами разработаны динамические чертежи для 34 заданий, большинство из которых мы заимствовали из книги А.Я. Цукаря «Развитие пространственного воображения» [2]. Поскольку реализация этих заданий на компьютере существенно отличается от той, что предложена в книге, мы внесли некоторые коррективы в их формулировки. В качестве примера приведем лишь следующие три задания.

Задание 1. На экране компьютера изображена фигура (рис. 1, левый слайд), разделенная на равные квадраты, один из которых окрашен. Выберите одну из шести прямых, двумя щелчками мыши задайте ее как ось симметрии, отразите окрашенный квадрат относительно этой прямой, окрасив тем самым новый квадрат. Попытайтесь окрасить всю фигуру.

Основная задача тех, кто конструирует динамический чертеж для этого задания, во-первых, сформулировать и корректно оформить на экране все необходимые инструкции по поводу используемых инструментов. Во-вторых, для тех, кто будет испытывать трудности с выполнением этого задания, разработать разумные визуальные подсказки. Так в обсуждаемом задании после нажатия на соответствующие кнопки-подсказки появляется ось симметрии s (красного цвета), которая, перемещаясь по плоскости, накла-

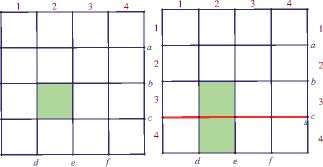
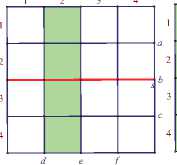
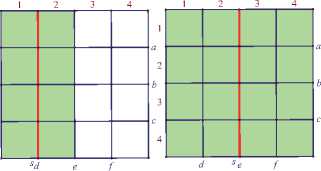
Рис 1. Этапы выполнения задания 1

дывается последовательно на прямые c, b, d и e, после чего окрашенные клетки отображаются относительно оси s (рис. 1, правые четыре слайда).

Отметим, что в задании 1 приведен наиболее простой вариант фигуры. Обучающиеся в процессе разработки восьми заданий, аналогичных заданию 1, предлагают свои версии фигур и различное расположение исходной окрашенной клетки.

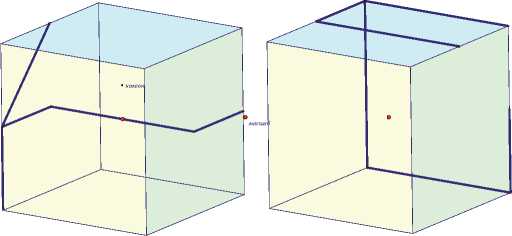
Задание 2. На экране компьютера изображены два равных куба и жирные линии на их поверхностях и внутри. Совместите мысленно эти кубы. Проекции совмещенной жирной линии на

поворот

Рис. 2. Слева изображены данные кубы, справа – кубы после их совмещения

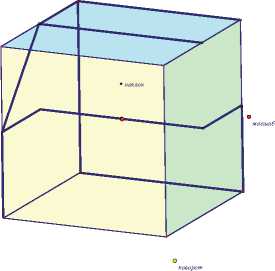
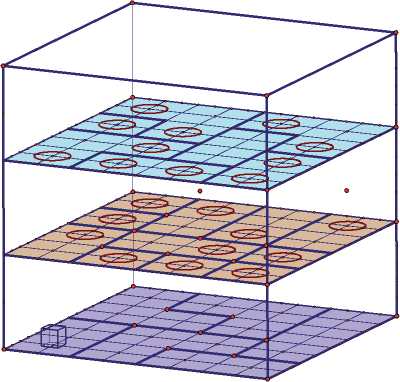
Рис. 3. Презентация путешествия кубика по лабиринту

переднюю грань, на правую грань и на верхнюю грань образуют слово из трех букв. Прочитайте его.

Чтобы сконструировать динамический чертеж для этого задания, достаточно воспользоваться готовым инструментом пользователя «Куб». Далее окрашиваются три его грани: передняя – желтым цветом, правая – зеленым цветом и верхняя – синим цветом. Чтобы изобразить второй куб, достаточно сначала на экран поместить любую точку – центр этого куба, затем задать вектор, начало которого совпадает с центром первого куба, а конец – с центром второго. Теперь осталось подсветить первый куб, воспользоваться параллельным переносом на этот вектор (команда «Перенести» из меню «Преобразования»), и на экране появится второй куб, равный первому (рис. 2). Кроме этого, он станет дублировать все преобразования, которые пользователь будет совершать с первым кубом (масштабирование, повороты и наклоны).

Теперь осталось выбрать на ребрах и гранях нужные точки и построить на первом и втором кубе требуемые жирные линии (окрашены синим цветом). Помощь разработчикам задания на этом этапе с удовольствием оказывают обучающиеся младших классов, не только подбирая слова из трех букв, благо в русском языке таких слов предостаточно, но и разбивая каждое слово на две компоненты – отдельно для каждого из кубов.

Если выполняющим это задание не удается мысленно совместить оба куба, а на первых порах в такой ситуации оказывается большинство школьников, то можно с помощью компьютерной мыши совместить центр второго куба с центром первого (рис. 2, правый слайд). Кубы не только совместятся, но и будут синхронно поворачиваться и наклоняться. В этом случае прочитать нужное слово не составит труда.

Задание 3. На экране компьютера изображен пространственный лабиринт с круглыми отверстиями, через которые проходит маленький кубик, расположенный на первом этаже лабиринта (рис. 3). С помощью компьютерной мыши можно перемещать кубик по каждому из трех этажей, не выходя за пределы многоугольников, отмеченных жирными линиями, либо перемещаться с этажа на этаж через круглое отверстие над (или под) кубиком. Найдите такую траекторию перемещения кубика, чтобы он прошел точно один раз через каждое отверстие.

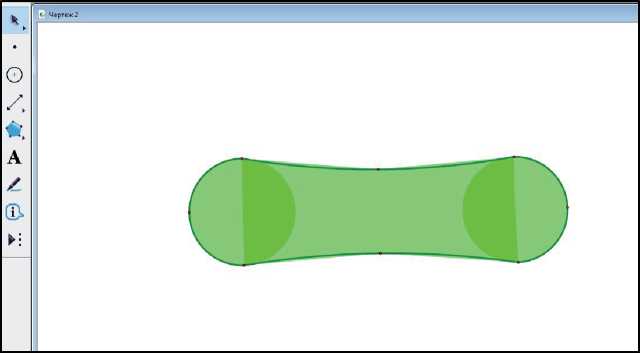
Рис. 4. Сноуборд из геометрических объектов

При конструировании динамического чертежа для этого задания используется собственный инструмент пользователя «Куб», знакомый ребятам по предыдущему заданию. Размеры куба делаются достаточно большими, во весь экран. Каждое вертикальное ребро куба делится на три равные части, создаются первый, второй и третий этажи. Используя инструмент «Деление отрезка на n равных частей», на каждом этаже изображается пол в клетку. В соответствии с устройством пространственного лабиринта в полу второго и третьего этажей создаются круглые отверстия, которые на модели изображаются в виде равных между собой эллипсов, центры которых находятся в заданных точках, а их сопряженные диаметры параллельны сторонам клеток. При наклоне куба автоматически изменяется и форма эллипсов. Например, если посмотреть на куб сверху, то отверстия будут круглыми.

Построение завершается конструированием маленького кубика, который, в отличие от предыдущего задания, после параллельного переноса большого куба уменьшается до нужных размеров.

При конструировании динамического чертежа для этого задания ученикам потребуется помощь учителя, хотя для построения всех требуемых фигур в среде «Живая математика» есть соответствующие инструменты. Как и во всех остальных заданиях создается кнопка-подсказка «Презентация путешествия кубика по лабиринту», нажав на которую, можно в режиме реального времени наблюдать за движением кубика по искомой траектории: как по каждому из трех этажей, так и при перемещении с этажа на этаж.

Задание 4. Задача: Из геометрических фигур составьте пригодный для занятий спортом «сноуборд».

Осуществлять построение «сноуборда» будем, используя свойства математического объекта: сноуборд, состоящий из геометрических объектов (2 одинаковые окружности, эллипс и 2 дуги, построенные по трем точкам). Используя инструмент «Построение окружности», находящийся на левой боковой панели инструментов, создадим окружность и построим любую прямую, проходящую через ее центр, с помощью инструмента «Отрезок»; параллельно построим отрезок АВ, зададим коэффициент сжатия отношением длин отрезков АВ к ВС; найдем середину отрезка АВ с помощью меню «Построение», находящегося на верхней панели инструментов, и выполним построение двух отрезков, затем с помощью стрелки (курсора) последовательно выделим их, перейдем в меню «Преобразования» и выберем команду, отмечающую соотношения; зададим произвольную точку на окружности, опустим из этой точки перпендикуляр на прямую, проходящую через центр окружности; построенную точку объявим центром окружности (двойным кликом мыши). Выделим произвольно построенную точку и выполним команду «Гомотетия», меню «Преобразования» верхней панели инструментов; для построенной в результате выполнения команды «Гомотетия» точки выполним команду «Геометрическое место точек» из меню «Преобразования», получим изображение эллипса.

Зададим нужный цвет и толщину линии, кликнув на выбранном объекте правой кнопкой мыши; по боковым точкам эллипса построим две одинаковые окружности путем их копирования, затем отметим по 3 верхние и нижние точки, выберем в меню «Построение» раздел «Построение дуги по выбранным трем точкам». На этом этапе правильный сноуборд, составленный из геометрических фигур, готов, далее необходимо скрыть ненужные элементы и раскрасить его на свое усмотрение.

Подводя итог, отметим, что разработанные динамические чертежи для большинства заданий прошли успешную апробацию на кружке «Экспериментальная математика» (научный руководитель – В.Р. Майер) для учащихся 7–9 классов в гимназии № 14 г. Красноярска. Все участники кружка успешно справлялись с выполнением заданий, а те из них, кто принимал участие в разработке некоторых заданий, заняли призовые места на Всероссийском конкурсе по экспериментальной математике (организатор – САФУ им. М.В. Ломоносова), требующем от участников высокий уровень пространственного воображения.

Как выяснилось, благодаря выполнению созданных в среде «Живая математика» заданий занимательного характера формируется не только пространственное воображение, но и абстрактное мышление, что весьма полезно при изучении стереометрии и решении задач прикладной направленности.