Корреляционный анализ результатов учебной деятельности студентов с дистанционной поддержкой процесса обучения

Реализация современных подходов к обучению в ВУЗах приводит к необходимости комбинирования традиционного обучения с дистанционным [2, c. 11; 7, c. 46]. Одной из причин такого сочетания стало сокращение аудиторных занятий при одновременном повышении требований к выпускникам. Как считают Е.В. Павлова и ГФ. Исламгулова, новые формы обучения в таких случаях просто необходимы [10, c. 85]. Преимущества онлайн-консультаций рассматривались ранее В.Р. Харпер, Г. Вильсоном, М.Е. Вайндорф-Сысоевой [5, c. 85], Р.Н. Бахтизиным [4, c. 11] и др. Развитие инфраструктуры дистанционного обучения идет достаточно быстрыми темпами [13, c. 120; 15, c. 7].

Для повышения качества обучения студентов первого курса математике [9, c. 231] авторами использовался курс дистанционной поддержки как элемент дополнения при очной форме обучения. Дистанционный курс позволяет обучающимся просматривать лекции, выполнять и сдавать на проверку домашние задания в удобное время, предварительно задавать вопросы, вызывающие затруднения, при самостоятельном изучении учебного материала. Системный подход к организации дистанционной поддержки, ежедневный контроль и постоянная коррекция курса позволяют обеспечивать мотивацию к изучению материала учебной дисциплины на достаточно высоком уровне, развивать мыслительную культуру, соответственно, увеличивать количество успевающих студентов [12, c. 117]. Благодаря внедрению онлайн-курса на аудиторных занятиях удалось уделить большее внимание изучению сложных тем. Это дало возможность прогнозировать результаты обучения с определенной точностью [14, c. 125]. Следует отметить, что самостоятельная работа обучающихся, использующих онлайн-курс, была организована более продуктивно и контролировалась более системно, чем у обучающихся, не использовавших такой курс.

В начале педагогического эксперимента авторами была выдвинута гипотеза о том, что применение подобного курса для контроля и мониторинга результатов достижений каждого студента и коррекция дальнейшего обучения в зависимости от результатов повлечет за собой увеличение количества успевающих студентов [6, с. 75]. Для эффективной работы онлайн-курса были задействованы эксперты, компетентные в области педагогики, и преподаватели, прошедшие повышение квалификации в области дистанционного обучения, учтена методология высшего образования, проводились постоянный мониторинг результатов и регулярная корректировка курса в зависимости от успехов и активности обучающихся [3; 8; 13; 1].

На первом этапе для определения наличия и характера статистической связи между количеством баллов за тест (Y) и количеством студентов, получивших определенное количество баллов (X), в виде корреляционных таблиц были подведены итоги тестирования по теме «Интегральное исчисление функции одной переменной» как студентов, не использовавших курс дистанционной поддержки, так и студентов, использовавших его. Затем составлены эмпирические законы распределения количества студентов (табл. 1 и табл. 2) и количества баллов в обоих случаях (табл. 3 и табл. 4).

По данным эмпирического закона распределения количества студентов, не пользующихся курсом дистанционной поддержки, и эмпирического закона распределения количества баллов этих студентов были вычислены средние значения = 1,35 и = 10,5 и средние квадратические отклонения σ²_Y= 1,9275, σ²_Х= 36,75. Аналогично вычислили средние значения = 1,3333, = 10,429 и средние квадратические отклонения o 2Y = 2,6035, о 2Х = 35,107. Вычислили условное среднее значение Y и условное среднее значение Х. По полученным данным установили средние значения количества баллов и количества студентов и их средние квадратические отклонения.

Корреляционный анализ результатов учебной деятельности студентов с дистанционной поддержкой процесса обучения

Общее

Курс дистанционно й подде ржки "Математика II семестр".

Цель курса: обеспечить базовую подготовку в области математических наук

Содержит лекции, презентации, интернет-ресурсы, разобранные примеры, задания для закрепления, индивидуальные задания по вариантам из контрольных работ тесты, итоговое повторение (тренажёр по математике), пробные варианты экзаменационных билетов, учебно-методический комплекс и контрольноизмерительные материалы, персональный консультант, список рекомендуемой литературы и интернет-ресурсов. видеолекции, график изучения материала, форум

Шварёва Етена Николаевна

График изучения

Новостной форум

Новостной форум

• *М Форум по работе в системе MOODLE

С Сайт кафедры ''математика'’

Рисунок 1. Фрагмент курса по дисциплине «Математика» для дистанционной поддержки первокурсников – бакалавров в образовательной среде Moodle

Таблица 1. Эмпирический закон распределения количества студентов, не пользующихся курсом дистанционной поддержки

Y	0	1	2	3	4
Распределение студентов по баллам	8	4	3	3	2
Относительная частота распределения студентов по баллам	0,4	0,2	0,15	0,15	0,1

И.А. Сокова, Е.Н. Шварева, Н.Ю. Фаткуллин, В.Ф. Шамшович

Таблица 2. Эмпирический закон распределения количества студентов, пользующихся курсом дистанционной поддержки

Y	0	1	2	3	4	5
Распределение студентов по баллам	9	5	3	1	1	2
Относительная частота распределения студентов по баллам	0,43	0,24	0,14	0,05	0,05	0,10

Таблица 3. Эмпирический закон распределения количества баллов тех студентов, которые не пользовались курсом дистанционной поддержки

X	1	3	5	7	9	11	3	5	17	19
Распределение баллов по студентам	2	2	2	2	1	2	2	2	2	3
Относительная частота распределения баллов по студентам	0,1	0,1	0,1	0,1	0,05	0,1	0,1	0,1	0,1	0,15

Таблица 4. Эмпирический закон распределения количества баллов тех студентов, которые пользовались курсом дистанционной поддержки

X	1	3	5	7	9	11	3	5	7	9
Распределение баллов по студентам	2	2	2	2	2	2	2	2	2	3
Относительная частота распределения баллов по студентам	0,10	0,10	0,10	0,10	0,10	0,10	0,10	0,10	0,10	0,14

Воспользовавшись данными корреляционных таблиц, вычислили коэффициенты уравнений эмпирических линий регрессий для данных обеих групп. Значения коэффициентов линий регрессий: 1) a = ρ_yx = ̶ 0,1395 и b = 2,8143 для

Y_p = P yyx Х + b и a = Р_ху = - 2,6589 и b = 14,089 для Х р = p yx Y + b (по итогам студентов, не пользующихся он-лайн-курсом);

• 2) a = p yx = -0,0922 и b = 2,2953 для

  Y_p = Рух Х + b и a = Р_ху= -1,2439 и b = 12,087 для Х р = p yx Y + b (по итогам студентов, пользующихся он-лайн-курсом).

Затем вычислили эмпирические линии регрессии Y=Y(X) и X=X(Y) для данных каждого года (Yx = aX + b и Xy = aY + b).

Значения коэффициентов линий регрессий: а = -0,13946 и а1= -2,65888 (2015 год) и a = ̶ 0,0922 и a1 = ̶ 1,2439 (2016 год).

Уравнения линий регрессий в обоих случаях:

• 1)    Y_cp= -0,1395 Х + 2,8143 и

  Х_р= - 2,6589 Y + 14,089 (по итогам студентов, не пользующихся онлайн-курсом);

• 2)    Y_cp= -0,0922 Х + 2,2953 и

  Х_ср ^{= -}1,2439 Y + 12,087 (по итогам студентов, пользующихся онлайн-кур-сом).

Изучение корреляционной связи между количеством студентов и итогами тестирования провели по следующим основным пунктам:

• 1)    определению формы корреляционной связи (вида теоретической функции регрессии) – линейной и нелинейной;

• 2)    определению тесноты (силы) корреляционной связи.

Представим графическое изображение эмпирических и теоретических линий регрессий У на Х (рис. 2-3).

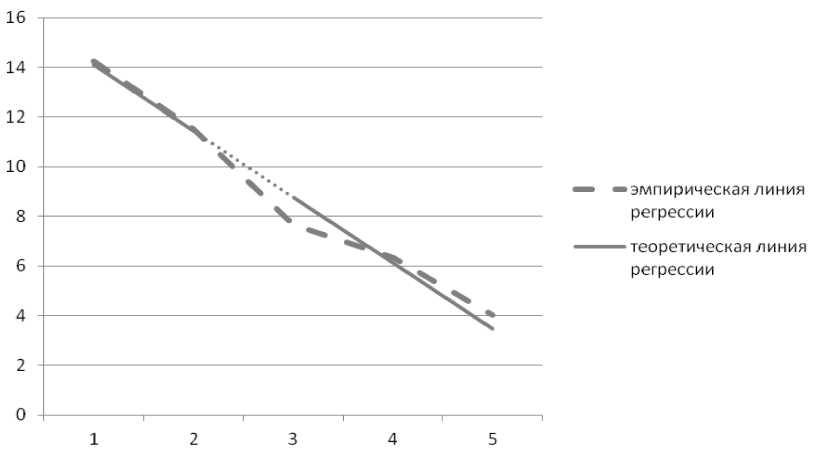
Рисунок 2. Графическое изображение эмпирических и теоретических линий регрессии У на Х (по итогам студентов, не пользующихся курсом дистанционной поддержки)

Корреляционный анализ результатов учебной деятельности студентов с дистанционной поддержкой процесса обучения

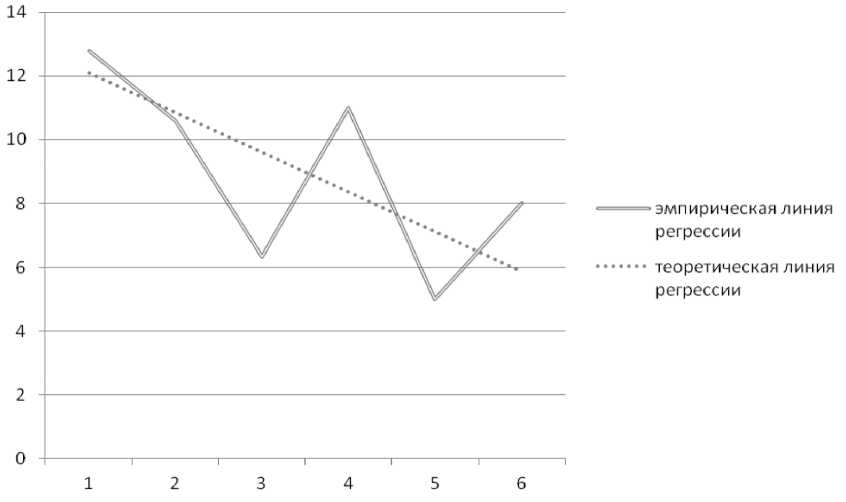
Рисунок 3. Графическое изображение эмпирических и теоретических линий регрессии У на Х (по итогам студентов, пользующихся курсом дистанционной поддержки)

И.А. Сокова, Е.Н. Шварева, Н.Ю. Фаткуллин, В.Ф. Шамшович

Определили эмпирические коэффициенты корреляции: r_b=ρ_yxσx/σy = –0.61 и r_b=ρ_yxσx/σy = –0,34.

Итак, коэффициент линии регрессии, равный –0,0922, в случае использования курса дистанционной поддержки, увеличился по сравнению с коэффициентом линии регрессии, равным –0,1395, в случае использования онлайн-курса. То есть количество студентов, получивших большее количество баллов, увеличилось, что указывает на положительное влияние дистанционной поддержки обучения. Соответственно, коэффициент корреляции тоже увеличился. Без использования онлайн-курса зависимость наших данных была обратная и достаточно тесная. При использовании курса зависимость была тоже обратной, но менее тесной. Выборочный коэффициент при этом вырос. Полученные результаты проведенного исследования дают основание предположить, что при совершенствовании онлайн-курса и более глубоком его внедрении коэффициент линии регрессии еще более возрастет. Таким образом, можно значительно увеличить количество успевающих студентов.

Необходимость дальнейшего совершенствования курса и расширение возможностей смешанного обучения оче- видна. Можно не ограничиваться только публикацией лекций и дублированием содержания практических занятий, но и продумать объяснение таких тем, которые обучающимся удобнее осваивать в свободном режиме с разной скоростью восприятия, не находясь в учебной аудитории. Дистанционный курс позволяет экспериментировать с компоновкой уроков и выявлять наиболее оптимальный вариант, который даст максимальный результат обучения, отражающийся в рейтинге студентов.