Математическое моделирование временного ряда количества преступлений в России

Кайбичев И.А.; Кайбичева Е.И.; Kabichev I.A.; Kaibicheva E.I.

Научные статьи \ Право. Юридические науки \ Уголовное право. Уголовное судопроизводство. Криминология. Криминалистика \ Криминология. Криминалистика

Математическое моделирование временного ряда количества преступлений в России

Автор: Кайбичев И.А., Кайбичева Е.И.

Журнал: Вестник экономики, управления и права @vestnik-urep

Рубрика: Математика

Статья в выпуске: 4 (49), 2019 года.

Бесплатный доступ

Предпринята попытка найти вид функциональной зависимости между числом преступлений на территории России и фактором времени. В процессе регрессионного анализа использованы наиболее известные функции, применяющиеся в экономике и биологии. В итоге выполненного исследования наиболее точное описание фактического количества преступлений в Российской Федерации получено в сплайновой модели с точками ДеМарко.

Математическая модель, количество преступлений, временной ряд, российская федерация

Короткий адрес: https://sciup.org/142226834

IDR: 142226834 | УДК: 343.9

Mathematical modeling of time series of crimes in Russia

An attempt is made to find a type of functional relationship between the number of crimes in Russia and the time factor. The regression analysis uses the most well-known functions used in economics and biology. As a result of the study the most accurate description of the actual number of crimes in the Russian Federation is obtained in the spline model with DeMarco points.

Текст научной статьи Математическое моделирование временного ряда количества преступлений в России

***

Возможность криминологического моделирования поднята в работе Т.В. Пилюгина, Д.А. Натура "Использование математи- ческого моделирования при прогнозировании региональной преступности в вопросах ее предупреждения" [См.: 1]. При этом рассмотрена региональная преступность на примере Краснодарского края, в частности данные с марта 2011 по февраль 2013 года для аппроксимации которых была использована линейная модель [2]. Анализ преступлений в Чикаго в период с 2001 по 2015 годы выполнен Вахрушевым [3]. При этом наилучшие результаты дала регрессия на основе случайных лесов.

Разработанная в исследовании [4] математическая модель позволяет прогнозировать количество преступлений на заданном периоде времени на основе рекуррентной формулы, которая позволяет рассчитать прогнозное значение на основании данных данного месяца за прошлый год и трех предше- ствующих месяцев рассматриваемого пери- ода.

Такая модель основана на предположении, что число преступлений зависит от времени. Эта гипотеза нуждается в проверке. Для этого выполним корреляционный анализ данных по числу преступлений в Российской Федерации за период 2001-2017 годов [5-21]. Расчет коэффициента линейной корреляции Пирсона привел к значению 0,68. У нас всего 17 значений данных

(n=17). При малом объеме выборки выполняют перерасчет коэффициента линейной корреляции Пирсона [22]:

R ‘ = R

1 - R 2

1 + 2(n-3)

Это дает результат R = -0,70. Имеем ситуацию средней связи.

Выполним проверку уровня значимости рассчитанного коэффициента корреляции. Выдвигаем две гипотезы: Н0 - временной зависимости числа преступлений нет (R =0), Н1 - такая связь есть (R ≠0).

Проверку нулевой гипотезы проводят с помощью преобразования Фишера [22]:

11+R′ u=2ln1-R′ =- 0,86

Полученное значение сравнивали с критическим uα(n) =z1-α2√n-3

Z, CL где - квантили нормированного распределения, zl-y =1,96 при уровне значимости α = 0,05 и zi-| =2,576 для α = 0,01. Для нашего случая имеем u0,01(18) =0,67, uo,os(18) =0,51. Выполняется неравенство |u| > ua(n), поэтому принимаем гипотезу Н1. Следовательно, мы установили на- личие временной зависимости числа преступлений с вероятностью 0,99.

Имеющийся статистический материал не дает возможность проверить результаты работы [4]. Однако имеющиеся данные можно интерпретировать с помощью регрессионного анализа. Для этого рассмотрим возможные классы функций.

Линейная модель

Связь между числом преступлений и фактором времени (задаваемом номером года) аппроксимируем прямой линией, коэффициенты которой рассчитаем с помощью регрессионного анализа [22]:

Y м = --72,1743*Х + 14738,3 (4)

где Yм - модельное количество преступлений (тыс. ед.), Х - номер года.

Реальные значения переменной Y, как правило, отличаются от модельных величин Yм, рассчитанных по функции регрессии (таб. 1).

Таблица 1

Линейная модель

Год	Y (тыс.)	Y м (тыс.)	e	e 2
2001	2968,3	3317,5	-349,2	121958,6
2002	2526,3	3245,4	-719,1	517034,9
2003	2756,4	3173,2	-416,8	173703,2
2004	2893,8	3101,0	-207,2	42933,0
2005	3554,7	3028,8	525,9	276540,8
2006	3855,4	2956,7	898,7	807744,0
2007	3582,5	2884,5	698,0	487232,1
2008	3209,9	2812,3	397,6	158081,3
2009	2994,8	2740,1	254,7	64856,1
2010	2628,8	2668,0	-39,2	1533,3
2011	2404,8	2595,8	-191,0	36474,4
2012	2302,2	2523,6	-221,4	49021,7
2013	2206,2	2451,4	-245,2	60139,8
2014 2015	2190,6 2388,5	2379,3 2307,1	-188,7 81,4	35592,5 6628,3
2016	2160,1	2234,9	-74,8	5596,7
2017	2058,5	2162,7	-104,2	10865,3
2018	1991,5	2090,6	-99,1	9813,4
среднее	2704,1	2704,0	0,0	159208,3

В качестве показателя качества регрессионной модели часто используют среднее значение квадрата ошибки e^2 = 1n^ ei2 (5)

i=1

В нашем случае среднее значение квадрата ошибки для линейной модели составило 159208,3 (Табл. 1).

Среднее значение ошибки равно 0. Коэффициент линейной корреляции Пирсона между ошибкой и номером года также равен 0. Это позволяет считать ошибку случайной величиной.

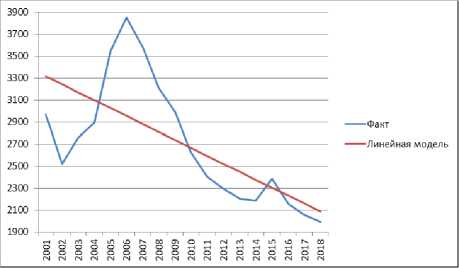
Рис. 1. Сравнение фактических значений с линейной моделью

Отметим, что линейная модель не может объяснить имеющийся максимум, приходящийся на 2006 год (Рис. 1).

Сплайновая модель

Используем аппроксимацию кусочнолинейной функцией, называемой в математике сплайном

277,6873 ∗ X - 553185,2001 ≤X ≤ 2006,,

-188,884 ∗ X + 382757,7 2006 <^ ≤ 2018. (6)

Y_М = ^

Сплайновая модель (Таб. 2) дает меньшее среднее значение квадрата ошибки (95696,9) по сравнению с линейной моделью (4).

Таблица 2

Сплайновая модель

Год	Y (тыс.)	Y м (тыс.)	e	e 2
2001	2968,3	2467,0	501,3	251338,2
2002	2526,3	2744,7	-218,4	47677,1
2003	2756,4	3022,3	-265,9	70723,1
2004	2893,8	3300,0	-406,2	165019,1
2005	3554,7	3577,7	-23,0	529,6
2006	3855,4	3855,4	0,0	0,0
2007	3582,5	3666,5	-84,0	7058,6
2008	3209,9	3477,6	-267,7	71679,9
2009	2994,8	3288,7	-293,9	86404,6
2010	2628,8	3099,9	-471,1	221899,5
2011	2404,8	2911,0	-506,2	256215,8
2012	2302,2	2722,1	-419,9	176310,3
2013	2206,2	2533,2	-327,0	106934,7
2014	2190,6	2344,3	-153,7	23631,1
2015	2388,5	2155,4	233,1	54317,1
2016	2160,1	1966,6	193,5	37459,6
2017	2058,5	1777,7	280,8	78865,1
2018	1991,5	1588,8	402,7	162178,3
среднее	2704,1	2805,5	-96,1	95696,9

Отметим, что среднее значение ошибки равно -96,1. Коэффициент линейной корреляции Пирсона между ошибкой и номером года также равен 0,227. Это не позволяет считать ошибку случайной величиной.

Cплайновая модель также корректно описывает максимум, приходящийся на 2006 год (Рис. 2).

Сплайновая модель с точками ДеМарка

В сплайновой модели [6] был смоделирован единственный максимум, приходящийся на 2006 год. В техническом анализе валютного и финансового рынков часто

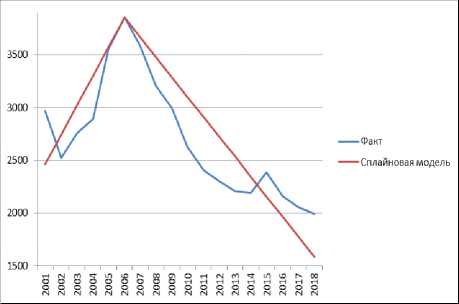
Рис. 2. Сравнение фактических значений со сплайновой моделью

применяют точки ДеМарка [23]. В таких точках значения меньше или больше двух соседних величин временного ряда. Среди фактических данных есть две точки минимума (2002 и 2014 год) и две точки максимума (2006 и 2015 год).

Рассмотрим аппроксимацию сплайновой функцией

Y М =

-442 ∗ X + 887410,3, ⎪^⎧ 332,275∗X-662688,

-208,1∗X+421304,

_⎪ 197,9∗X-396380, ⎩-129,238∗X+262802,4,

2001 ≤ X ≤ 2002,

2002 < X ≤ 2006, 2006<^ ≤ 2014, (7) 2014<^ ≤ 2015,

2015 < ^ ≤ 2018.

Использование точек ДеМарко (Таб. 3) уменьшило среднее значение квадрата ошибки до 37818,8.

Отметим, что среднее значение ошибки равно -132,2. Коэффициент линейной корреляции Пирсона между ошибкой и номером года также равен -0,055. Это позволяет считать ошибку случайной величиной.

Таблица 3

Сплайновая модель с точками ДеМарко

Год	Y (тыс.)	Y м (тыс.)	e	e²
2001	2968,3	2968,3	0,0	0,0
2002	2526,3	2526,3	0,0	0,0
2003	2756,4	2858,6	-102,2	10439,7
2004	2893,8	3190,8	-297,0	88238,7
2005	3554,7	3523,1	31,6	997,0
2006	3855,4	3855,4	0,0	0,0
2007	3582,5	3647,3	-64,8	4199,0
2008	3209,9	3439,2	-229,3	52578,5
2009	2994,8	3231,1	-236,3	55837,7
2010	2628,8	3023,0	-394,2	155393,6

2011	2404,8	2814,9	-410,1	168182,0
2012	2302,2	2606,8	-304,6	92781,2
2013	2206,2	2398,7	-192,5	37056,3
2014	2190,6	2190,6	0,0	0,0
2015	2388,5	2388,5	0,0	0,0
2016	2160,1	2259,3	-99,2	9833,2
2017	2058,5	2130,0	-71,5	5115,8
2018	1991,5	2000,8	-9,3	86,2
среднее	2704,1	2836,3	-132,2	37818,8

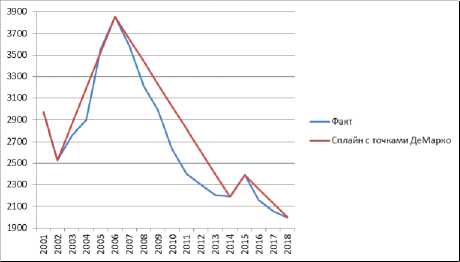
Рис. 3. Сравнение фактических значений со сплайновой моделью с точками ДеМарко

Заметим, что учет точек ДеМарко позволил более точно смоделировать фактические данные (Рис. 3).

Модель Ферхюльста

Для аппроксимации нашей ситуации используем функцию Ферхюльста которая часто используется в биологии для описания динамики популяции [24]:

93396,71 8

^{YМ =} 3417,3 - 3390,0 ∗ exp(-0,00235 ∗(X-2000)) (8)

Отметим, что среднее значение ошибки равно -11,3 (Таб. 4). Коэффициент линейной корреляции Пирсона между ошибкой и номером года также равен -0,118. Это позволяет считать ошибку случайной величиной.

Таблица 4

Модель Ферхюльста

Год	Y (тыс.)	Y м (тыс.)	e	e 2
2001	2968,3	3320,5	-352,2	124041,4
2002	2526,3	3229,1	-702,8	493865,0

2003 2004	2756,4 2893,8	3142,5 3060,6	-386,1 -166,8	149101,3 27806,1
2005	3554,7	2982,8	571,9	327122,6
2006	3855,4	2908,8	946,6	895995,2
2007	3582,5	2838,5	744,0	553539,5
2008	3209,9	2771,5	438,4	192193,1
2009	2994,8	2707,6	287,2	82478,1
2010	2628,8	2646,6	-17,8	317,3
2011	2404,8	2588,3	-183,5	33677,7
2012	2302,2	2532,5	-230,3	53058,2
2013	2206,2	2479,1	-272,9	74494,8
2014	2190,6	2427,9	-237,3	56334,5
2015	2388,5	2378,8	9,7	93,3
2016	2160,1	2331,7	-171,6	29444,7
2017	2058,5	2286,4	-227,9	51933,5
2018	1991,5	2242,8	-251,3	63162,3
среднее	2704,1	2715,3	-10,7	178258,8

Модель Ферхюльста дала наибольшее среднее значение квадрата ошибки (178258,8). При этом модельные результаты заметно отличаются от фактических (Рис. 4).

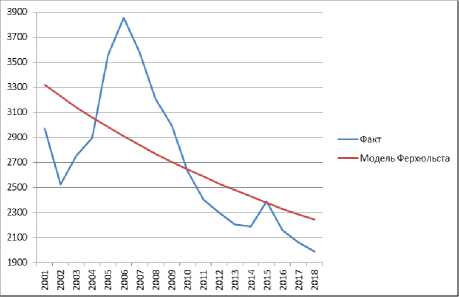
Рис. 4. Сравнение фактических значений с моделью Ферхюльста

В итоге выполненного исследования наиболее точное описание фактического количества преступлений в Российской Федерации получено в сплайновой модели с точками ДеМарко.

Предложенная математическая модель числа преступлений в Российской Федерации может быть использована для прогнозирования.

Список литературы Математическое моделирование временного ряда количества преступлений в России

Пилюгина Т.В., Натура Д.А. Использование математического моделирования при прогнозировании региональной преступности в вопросах ее предупреждения // Всероссийский криминологический журнал. 2017. Т. 11. № 1. C. 61-70.
Пилюгина Т.В., Пичкурено Т. А., Вендина А.А. Математические методы прогнозирования преступности // ASPECTUS. 2015. № 1. С. 98-103.
Вахрушев А.А. Прогнозирование уровня преступности на основе статистических данных: Магистерская диссертация. СПб: Санкт-Петербургский университет, 2016. 37 с.
Айкожаев Н.М., Шестопалова О.Л. Математическая модель прогнозирования динамики преступлений // Научное сообщество студентов XXI столетия. Технические науки: сб. ст. по мат. XLIV междунар. студ. науч.-практ. конф. (Россия, Новосибирск, 26 июля 2016 г.). 7(43). https://sibac.info/archive/technic/7(43).pdf
Российский статистический ежегодник 2003. Стат. сб. М.: Госкомстат России, 2003. 705 С.
Российский статистический ежегодник 2004. Стат. сб. М.: Росстат, 2004. 725 с.
Российский статистический ежегодник 2005. Стат. сб. М.: Росстат, 2005. 819 с.
Российский статистический ежегодник 2006. Стат. сб. М.: Росстат, 2006. 806 с.
Российский статистический ежегодник 2007. Стат. сб. М.: Росстат, 2007. 825 с.
Российский статистический ежегодник 2008. Стат. сб. М.: Росстат, 2008. 847 с.
Российский статистический ежегодник 2009. Стат. сб. М.: Росстат, 2009. 785 с.
Российский статистический ежегодник 2010. Стат. сб. М.: Росстат, 2010. 813 с.
Российский статистический ежегодник 2011. Стат. сб. М.: Росстат, 2011. 795 с.
Российский статистический ежегодник 2012. Стат. сб. М.: Росстат, 2012. 786 с.
Российский статистический ежегодник 2013. Стат. сб. М.: Росстат, 2013. 717 с.
Российский статистический ежегодник 2014. Стат. сб. М.: Росстат, 2014. 693 с.
Российский статистический ежегодник 2015. Стат. сб. М.: Росстат, 2015. 728 с.
Российский статистический ежегодник 2016. Стат. сб. М.: Росстат, 2016. 725 с.
Российский статистический ежегодник 2017. Стат. сб. М.: Росстат, 2017. 686 с.
Российский статистический ежегодник 2018. Стат. сб. М.: Росстат, 2018. 694 с.
21.Число зарегистрированных преступлений по видам. URL: http:// www.gks.ru/ Население/ Правонарушения / Основные показатели преступности / 10-01.doc.
Харченко М.А. Корреляционный анализ: Учебное пособие для вузов. Воронеж: Издательско-полиграфический центр Воронежского государственного университета, 2008. 31 с.
ДеМарк Т.Р. Технический анализ новая наука. М.: Изд-во "Евро", 2012. 178 с.
Соколов С.В. Модели динамики популяций: Учеб. пособие. СПб.: Изд-во СПбГЭ-ТУ «ЛЭТИ», 2018. 61 с.

Еще