Методические основы задачного подхода к процессу обучения младших школьников математике

Социальные преобразования, происходящие в современном обществе, выявили определенные противоречия, связанные с изменением социально-значимых критериев в рамках образовательной системы. Развитие теории и практики образования обусловило новые требования к характеру и содержанию педагогической деятельности и индикативно-факторной интерпретации педагогической практики. Они имеют принципиальное значение и обязывают рассматривать во взаимосвязи и взаимодействии деятельность педагога и деятельность учащихся. В рамках этих требований становится актуальным задачный подход к процессу обучения, выражающийся в переоценке роли ученика как субъекта этого процесса.

Смена парадигмы образования, инициированная созданием теории развивающего обучения, определила характер взаимодействия двух деятельностей (учителя и учащихся) в этом процессе. Направленность деятельностей на решение системы задач: математической, учебной, методической – является концептуальной методической основой задачного подхода к процессу обучения. Таким образом, обучение можно рассматривать как процесс решения системы различного рода задач1. Рассмотрение задачи в структурном контексте как единство цели и условия (или цели в заданных условиях)2, посредством сопоставительного анализа позво-

Кочеткова Ирина Александровна, кандидат педагогических наук, доцент кафедры математики, естествознания и методик их преподавания.

лит определить соотношение целевого и задач-ного подходов в обучении.

Задачный подход имеет вектор стратегической направленности на построение системы основополагающих задач (математической, учебной, методической) для решения проблем связанных с обучением и развитием младших школьников. Происходит перенос акцентов на овладение учащимися состава обобщенного формируемого способа решения различного рода задач, выполняющих функцию метода учения и создание необходимых условий для его формирования. Это позволяет мотивировать, планировать учебную деятельность учащихся и одновременно создавать условия для выполнения этой деятельности и достижения ее результата, т.е.вносить четкость и системность в организацию процесса обучения.

Однако, из психологии известно, что успешность решения различного рода задач во многом зависит от условий, в которых они решаются. Этими условиями являются субъективные характеристики учащихся: особенности восприятия, памяти, внимания, усвоения единиц учебной информации и т.д. Так, выделяются пять уровней усвоения учебного материала: различение-уровень знакомства; запоминание-уровень неосознанного воспроизведения; понимание-уровень осознанного воспроизведения; элементарные умения и навыки – репродуктивный уровень, т.е. умение пользоваться полученными знаниями при решении типовых задач; перенос сформированных умений в новые ситуации – уровень творческого применения умений, способов учебных действий. На каждом из этих уровней развертывается целенаправленная субъективная деятельность учащихся по решению задачи. Но задача не существует вне проблемной ситуации, в которой должен действо- вать ученик то, что составляет задачу для одного, может не быть задачей для другого. Поэтому, в этом случае, невозможно объективное изучение задач, независимо от рассмотрения деятельности ученика, от закономерностей процесса усвоения. Учет основных закономерностей (инвариантных характеристик процесса), отражающих причинно-следственные связи и зависимости, позволяет прогнозировать процесс усвоения конкретного математического содержания. К ним относятся: психологические закономерности восприятия, памяти, внимания, мышления и общие дидактические закономерности обобщения, свертывания действия, взаимно-обратных действий, обучения в сходных условиях, зависимости условий и операционного состава действий, возрастание роли несущественных компонентов математических объектов, тормозящего влияния данной функции объекта, инерции действия.

Раскроем дидактические закономерности: 1) закономерность обобщения – обобщение успешно идет по тем признакам, которые входят в ориентировочную основу формируемого действия с данными объектами; 2) закономерность свертывания действия – общая закономерность усвоения сложных действий, в результате которого происходит свертывание действия путем выпадения обосновывающих его положений и промежуточных операций, входящих в это действие; у учащихся образуются умственные связи – ассоциации, объединяющие начальное и конечное звено формируемого действия, т.е. его цель; 3) закономерность взаимно-обратных действий – формирование прямого действия не предполагает одновременного с ним формирования обратного действия; 4) закономерность обучения в сходных условиях – при изучении нового сходного действия, отличающий его компонент является слабо-сигнальным или же несигнальным для учащихся; 5) закономерность зависимости условий и операционного состава действий – изменение условий выполнения действий влечет за собой и изменение его операционного состава; 6) закономерность возрастание роли несущественных компонентов математических объектов – многократное сочетание индивидуальных признаков с общими существенными признаками того же объекта влечет за собой то, что эти индивидуальные признаки воспринимаются как существенные; 7) закономерность тормозящего влияния данной функции объекта – данная в условии функция объекта, его внешняя особенность или отношения оказывают тормозящее влияние на выявление другой функции того же объекта; 8) закономерность инерции действия – однотипные, по- вторяющиеся задания снижают степень осознания формируемого действия.

Опора на психологические и дидактические закономерности позволяет изучить основной механизм исследования задачи – процесс ее решения. Процесс решения задачи представляет собой такую систему преобразований условия задачи, при котором достигается требуемое искомое. Фактически в большинстве случаев решение задачи – процесс преобразования некоторой начальной (заданной) ситуации в некоторую конечную (требуемую) ситуацию. Поэтому, для полноценного исследования проблемы на методическом уровне необходимо рассмотреть сами задачи, установить их особенности, определить их место, роль и функции в обучении, классифицировать задачи по видам, изучить их взаимосвязь и влияние на процесс усвоения математического содержания. Обучение следует рассматривать как процесс решения целостной системы взаимосвязанных и взаимозависимых задач: математической (предметной), учебной и методической. Такой подход к обучению (за-дачный подход) позволяет изучать и формировать особый вид деятельности, при котором появляется возможность описывать и проектировать деятельность ученика и деятельность учителя как систему процессов решения разных видов задач. В процессе обучения происходит взаимодействие двух видов деятельностей учителя и ученика (т.е. взаимодействие внешних и внутренних факторов), которые можно описать через постановку и механизм решения системы трех взаимосвязанных задач. Эта исходная система задач позволяет модернизировать методическую модель системы обучения в рамках за-дачного подхода3.

Таб. 1. Сопоставительный анализ целевого и задачного подходов

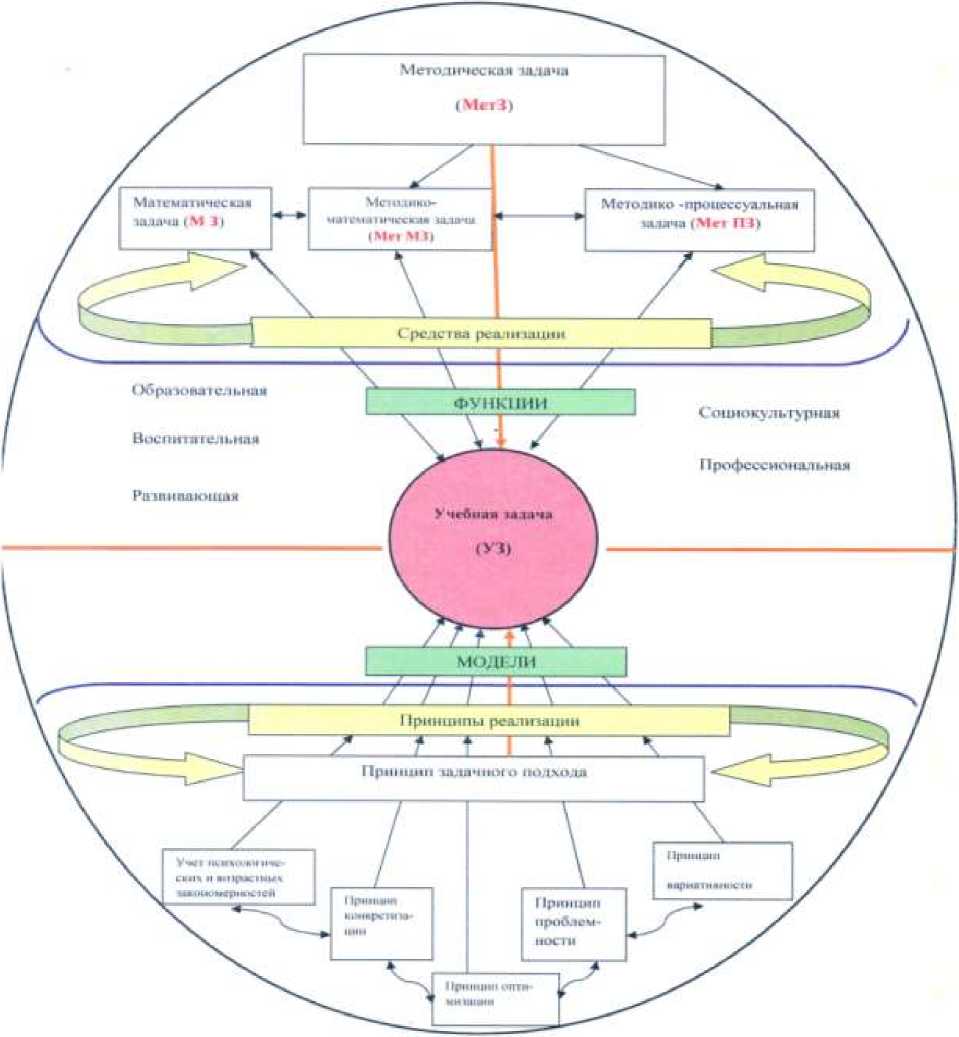
Рис. 1. Модель методической системы обучения как системы задач

Построение методической модели как системы задач обладающей свойствами полноты, целостности, структурности и взаимосвязанности является на наш взгляд актуальной проблемой современного школьного образования. Полнота определяется охватом всех видов задач; взаимосвязанность – есть зависимость каждого структурного компонента от его места и функции внутри системы; целостность системы определяется тем, что все компоненты обеспечивают решение единой учебной задачи как системообразующего компонента системы⁴. В качестве методико-процессуальных основ ее реализации выделены: теория обучения, деятельностный подход к обучению, психолого-дидактические закономерности, методические принципы, методы и формы организации деятельности учащихся.

Дальнейшая детализация позволила определить основные функции модели: социокультурная (общекультурная), образовательная, воспитательная, развивающая, профессиональная и методические принципы функционирования модели методической системы: принцип задачного подхода (введение учащихся в ситуацию учебной задачи посредством методических задач), принцип проблемного подхода (самостоятельное «добывание» учеником знаний, открытие нового понятия, способа действия и его использование в обучении), принцип вариативного подхода («перенос» освоенного обобщенного способа действия в новые условия, на другое содержание), принцип оптимизации (получение эффективного результата обучения с наименьшими временными затратами), принцип конкретизации (взаимосвязь теории и практики посредством применения теоретических положений в педагогической деятельности), принцип учета психологических и возрастных закономерностей в процессе обучения.

Такая модель методической системы позволяет рассмотреть все содержание начального курса математики как систему задач, каждая из которых выполняет определенные функции на этапах обучения. Реализация задачного подхода позволяет, учитывая психологические возрастные особенности детей младшего школьного возраста мотивировать их деятельность, создавать условия для решения задач «в зоне ближайшего развития», овладевать математическими понятиями, свойствами, открывать новые способы действий, контролировать и оценивать свои действия, т.е. формировать учебную деятельность младшего школьника поэтапно, в соответствии с ее структурными компонентами. В рамках этой системы создаются широкие возможности для формирования спецификоматематических и общеинтеллектуальных компетентностей, которые являются необходимым и очень важным компонентом, как деятельности учащихся, так и профессиональной подготовки учителя.

METHODOLOGICAL PRINCIPLES OF PROBLEM APPROACH TO MATHEMATICS TRAINING FOR YOUNG SCHOOLCHILDREN