Оценка сейсмических рисков на туристско-рекреационных территориях: математические модели

Прогноз сейсмического риска, выступая важной частью комплексного прогноза геоэкологической обстановки, является одной из зло- бодневных проблем современности, имеющей не только научное, но и серьёзное практическое значение для развития туризма и рекреационной деятельности [1–4]. Фактор сейсмического риска серьезно тормозит развитие туризма и строительство рекреационных объектов во многих регионах нашей страны и мира вследствие непредсказуемости земных катастроф и боязни путешествующих попасть в зону их проявления [5]. Во многом из-за непредсказуемости опасных «сюрпризов» Земли в научный оборот введено понятие “медленная” катастрофа [6 9]. Поэтому необходимость скорейшего решения проблемы прогноза сейсмических рисков, связанных с землетрясениями, неуклонно возрастает, поскольку проводимые многими странами исследования говорят о том, что география сейсмической опасности не ограничивается общеизвестными высокосейсмичными зонами, но и охватывает многие регионы, ранее считавшиеся малосейсмичными и даже асейсмичными [10; 11].

В XX веке предпринимались интенсивные международные попытки решить столь опасную для человечества проблему, однако они не увенчались каким-либо значимым успехом.

Так, по оценкам В.И. Кейлис-Борока и его соавторов [12] , существующие системы прогноза землетрясений способны обеспечить следующие грубые оценки точности его характеристик:

• 1)    место готовящегося землетрясения – сотни километров;

• 2)    возможная энергия ожидаемого землетрясения – шесть порядков;

• 3)    время реализации – годы.

Совершенно очевидно, что такой прогноз никакой практической ценности не имеет для оценки сейсмической опасности туристско-рекреационных (где всё более часто происходят катастрофические землетрясения) и заселенных территорий. Помимо того, что он может порождать ложную тревогу, он также способен породить и ложную успокоенность. Именно это произошло в 1989 г. в Калифорнии, когда сильное землетрясение ожидали в Паркфилде (300 км от Сан-Франциско), а оно произошло непосредственно под Сан-Франциско.

В последние десятилетия в геофизике господствовали два кардинально противоположных подхода к оценке сейсмического риска.

Первый подход основан на прямом методе обнаружения местоположения очага готовящегося землетрясения – деформационно-геодезическом методе, который позволяет, как полагают его приверженцы, осуществлять точный прогноз места этого очага и определять максимально возможную силу будущего землетрясения. Однако этот метод, не неся большого потенциала в разрешении задачи прогнозирования, сопряжён со значительными материальными и финансовыми затратами: в идеале все более или менее опасные в сейсмотектоническом отношении регионы должны быть опутаны сетью прогнозных профилей, что само по себе представляет трудновыполнимую задачу.

Второй подход основан на идеях обнаружения очага и отслеживания происходящих в нём процессов по разрозненным косвенным признакам – аномалиям, порождаемым готовящимся очагом в различных полях: сейсмических, деформационных, гидрогеологических, геохимических, электромагнитных и других. Конечно, есть веские основания полагать, что в однородной изотропной среде местоположение готовящегося очага действительно можно было бы точно локализовать по подобным аномалиям, однако реальная среда неоднородна и неизотропна. Именно эти качества реальной среды и не позволяют приемлемо решить проблему прогноза землетрясений.

Ясно одно: проблемы защиты населения и территорий, в том числе ТРТ, от воздействия опасных сейсмических процессов невозможно решать, не владея информацией об их пространственном распределении, интенсивности воздействия и периодичности проявления.

Для этой цели необходимо объединение обоих методов, из которых нужно взять самое ценное, достоверное, научно обоснованное и перевести это на язык математических моделей.

Комплексная математическая модель оценки сейсмического риска

Рассматриваемая в настоящей статье математическая модель оценки сейсмической устойчивости территорий представляет собой синтез двух конкурирующих подходов к оценке сейсмического риска, господствующих в настоящее время в геофизике, то есть объединяет в одной модели факторы влияния возмущений в геосреде, определяемым по косвенным признакам, в нашем случае – по аномальному гравитационному полю (вертикальная составляющая возмущений) [13–15] и современным движениям земной коры, основанным на данных повторных геодезических измерений, в частности, по данным космической геодезии (горизонтальная составляющая).

Для иллюстрации сказанного отвлечёмся на некоторое время от реальной геологической сре- ды и представим себе однородное изотропное замкнутое упругое пространство в форме параллелепипеда – некоторую «плиту» с известными осреднёнными значениями плотности, модуля сдвига и модуля Юнга.

Также предположим, что эта среда («плита») рассматривается в рамках ньютоновской реологии. И на неё снизу вверх, строго в вертикальном направлении, действует некоторая распределённая нагрузка P(x, y) (аномальное гравитационное поле). В горизонтальном направлении, фиксируемая по данным измерений, действует нагрузка V(x, y) (смещения в геосреде), которые и образуют совместное внешнее воздействие на геосреду (рис. 1). В результате такого воздействия в изотропной среде («плите») возникают неоднородные по своей структуре поля напряжений и смещений.

В таком случае, например, распределённое внешнее воздействие P(x, y) , известные дискретные значения которого заданы с некоторым фиксированным шагом по осям X и Y , представляются в виде ряда (1), то есть выполняется разложение аномального гравитационного поля в изостатической редукции на составляющие его зональные гармоники

^{P (} x , У ) = p^T- ^{+ 1} L Pm 0 ⁺

• ^{4    2} m = 1

l      sl

+ 1 L p 0 n + LL p

² n = 1          m = 1 n = 1

где, например,

P mn = a mn cos k x x cos k y y ⁺ b mn sin k x x cos k_yy ^{+ +} c mn ^cos k x x ^{sin к} у У ⁺ d mn sin ^k x x sin ^к у У

a mn

4 a b

=— Jj p ( x , y )cos k x x cos k ydxdy ;

ab

nm    nn

;             ; a , b – соответственно

x a yb, длина (X) и ширина (Y) рассматриваемой территории; p(x,y) – величины изостатических аномалий гравитационного поля.

Распределенная горизонтальная нагрузка

V(x, y) в таком случае также должна быть представлена в виде подобного ряда (1).

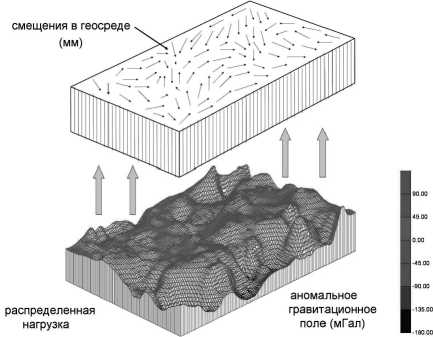
Рис. 1. Физическая модель возникновения напряжений и смещений в упругом объеме геосреды при вертикально-горизонтальных возмущениях

Тогда компоненты тензора напряжений и составляющие вектора смещений в геосреде представляются аналогичным образом, например, для нормальных компонент тензора напряжений соотношениями вида (2):

CTp (x, y, z) = -c/p } '^Xn'..m + lsl

+1Lc? n) +LTC”),(2)

² n = 1            m = 1 n = 1

где в € { X, y, Z , } .

Сформулируем граничные условия предложенной модели. Предположим, что к нижней поверхности упругого слоя приложена вертикальная распределенная нагрузка, а сдвиговые напряжения в вертикальных профилях на верхней и нижней поверхностях слоя равны нулю. В таком случае граничные условия для модели будет выглядеть следующим образом:

'c >^{( ( x} , y ^,0) = P ^{( x} , y ), ^ xy ( x , y , h ) = ^ V ( x , y ), ^T xz ^{( x} , у , h ) = ⁰, ^T xz ^{( x} , У ^,0) = ⁰

Подставив в систему (3) выражения для соответствующих компонент тензора напряжений, получим следующую систему равнений для отыскания коэффициентов A, B, C, D:

k2⎜ μ D -kA ⎟cosk xcosk y = P cosk xcosk y, x  ykx  y

_{⎝ λ +} μ       _⎠ x y k x y

- kxky {[k (B + Dh)+ C]shkh + [k(A + Ch)+ D]chkh}sinkxxsinkyy = μVk sinkxxsinkyy, kkx⎨

k ( A + Ch ) +

λ λ + μ

D

shkh +

k ( B + Dh ) +

λ _C λ + μ

⎥ chkh ⎬ sin k_xx cos k_yy = 0,

kk_x ⎜ kB +

λ λ + μ

C ⎟ sin k x cos k y = 0.

xy

Разрешая указанную систему уравнений относительно неопределенных коэффициентов, получим соотношения для компонент тензора напряжений и составляющих вектора смещений в геосреде, на основании которых и выполняется расчет её сейсмической устойчивости.

Результаты модельной оценки сейсмических рисков

Рассмотрим результаты математического моделирования, выполненного на основе вертикально-горизонтальной региональной модели оценки сейсмической устойчивости геосреды.

Эта модель реализована для целого ряда регионов России (Прибайкалье, Приморский и Хабаровский края, Рязанская область) и зарубежных стран (Коста-Рика, Турция, Эквадор), где особое внимание уделяется развитию турист ско-рекреационного комплекса [16–18].

В настоящей статье для примера приведены результаты модельной оценки сейсмических рисков для масштабного региона, включающего в себя часть территории Азербайджана, Армении, Грузии, Ирака, Ирана, России, Турции, Сирии (рис. 2).

Как видно из рисунка, именно на этих территориях, включающих теплые южные моря (Чёрное, Каспийское и Средиземное) с многочисленными курортными зонами, влекущими миллионы туристов, сейсмические риски весь- ма велики, и их необходимо учитывать при организации туристско-рекреационной деятельности в вышеназванных государствах. На карте территории, оконтуренные изолиниями до 0.3, являются зонами низкого риска; от 0.3 до 0.5 – среднего; от 0.5 до 0.8 – высокого; более 0.8 – катастрофического риска. Карта показывает достаточно высокую точность используемой модели, включая исторический аспект земных катастроф (их эпицентры отмечены красным цветом).

Для оценки сейсмических рисков взят достаточно значительный по масштабу регион таким образом, чтобы озеро Ван оказалось в его центре. Авторы при этом располагали информацией о современных горизонтальных движениях земной коры по данным космической геодезии. Поэтому была проведена дополнительная проверка модели на основании сопоставления ориентации векторов горизонтальных смещений на поверхности, полученных в результате математического моделирования, с информацией о современных движениях земной коры по данным космической геодезии. Соответствующая карта представлена на рис. 3. Анализируя её, нетрудно видеть, что наибольшие сейсмические риски, как правило, характерны тем местам исследуемой территории, где векторы горизонтальных смещений имеют противоположную направленность, либо характеризуются спиралевидной направленностью.

Рис. 2. Карта эквипотенциального распределения вероятностного показателя комплексного геодинамического риска с эпицентрами произошедших в рассматриваемом регионе землетрясений с магнитудой от 5 до 7,8 с 1900 г. по 2010 г. [41].

Перспектива развития модели: учет релаксации напряжений и деформаций

Рассмотренная математическая модель описывает распределение смещений, напряжений и деформаций в геосреде, отвечающей законам ньютоновской реологии, то есть без диссипации энергии. Между тем, в реальности, особенно для прогностических оценок, необходимо учитывать влияние релаксации напряжений и деформаций на скорость их накопления в данной геосреде.

Как известно, в земной коре в условиях сжатия процесс разрушения происходит по схеме сдвига [19]. Оценка прочности среды в таком случае производится на основании следующего положения. Пластическая деформация, предваряющая разрушение, начинается при определенном значении объемной плотности потенциальной энергии формоизменения, так как при пластической деформации в среде невозможно ее накопление больше определенного предела прочности. Пластическая деформация, предваряющая разрушение, не наступит до тех пор, пока плотность энергии формоизменения не превысит предела прочности для определенного типа пород земной коры.

Если скорость накопления упругой деформации очень мала, то напряжения будут релаксировать, и в этом случае энергия упругих деформаций будет диссипировать, переходя в тепло и энергию полиморфических и физико-химических процессов метаморфизма, и только малая ее часть будет накапливаться [15].

Рассмотрим процесс нарастания деформации в среде, обладающей не только упругостью, но и вязкостью. Примем, что скорость деформации является величиной постоянной. Связь между сдвиговым напряжением и деформацией для упруго-вязкой среды (в плоскости XZ ) определяется уравнением

+   τ xz ⁼       ,

μ dt η dt

где γ _xz

1 ⎜⎛ ∂ux2 ⎝ ∂z

+

∂uz ⎟⎞ ∂x ⎠

– деформация;

τ_xz – сдвиговое напряжение; μ – модуль сдвига; η– динамическая вязкость среды.

Рис. 3. Распределение векторов горизонтальных смещений на поверхности, полученных по результатам математического моделирования.

dγ

Обозначая для удобства ^xz

dτ                   dt xz = τ , перепишем (5) в виде dt xz

τ′ τ xz xz ′

+    = γ _xz ^.

μη

γ ′  и xz

Выражение (6) представляет собой обыкновенное дифференциальное уравнение первого порядка (так как скорость деформации постоянна), и его решение записывается в виде:

где δ = η µ – время релаксации напряжений, определяемое через модуль сдвига и динамическую вязкость среды.

Очень важным является вопрос об оценке величины скорости деформации γxz . Для этого выведем формулу для оценки скорости деформации γ′xz в вертикальной плоскости XZ. Вывод основан на предположении, что деформации и, соответственно, сдвиговые напряжения являются функциями упругих и вязких свойств гео- среды.

Ввиду того, что мы не знаем истинную величину «весового» вклада упругой и вязкой компо- нент геосреды, примем для простоты расчетов, что этот вклад применительно к параметрам её упругих и вязких свойств одинаков, получим формулу для приближенной оценки скорости деформаций γ ′ с учетом релаксации:

xz

γ ′ _xz

xz

,

T (°)

где T xz — начальное сдвиговое напряжение;

δ ₌ η μ – время релаксации; t – время.

С использованием соотношения (8) скорость деформации сдвига может быть оценена через начальное сдвиговое напряжение, параметры упруго-вязкой среды и время, прошедшее от начала накопления деформаций сдвига.

Таким образом, рассмотренная в статье комплексная математическая модель оценки сейсмической устойчивости геосреды, базирующаяся на совместном учете влияния возмущений в этой среде, определяемым как по аномальному гравитационному полю, так и по современным движениям земной коры, основанным на данных повторных геодезических измерений, позволяет более достоверно, по сравнению с так называемыми вертикальными моделями, выявлять на исследуемых территориях участки, наиболее опасные в сейсмическом отношении.

Еще больших результатов можно добиться при использовании описанной модели, если в ней будет рассматриваться максвелловская реология среды, позволяющая учесть влияние релаксации напряжений и деформаций на скорость их накопления в данной среде. Такой подход может позволить выполнить количественные оценки диссипации сейсмодеформационной энергии, что является очень значимым в плане осуществления прогнозных оценок сейсмичности во временном аспекте.

Заключение

Проблемы оценки геоэкологических рисков на туристско-рекреационных территориях во многом связаны с учетом системного влияния тектонических разломных нарушений верхних слоев земной коры [20]. Настоящая статья выступает скромным вкладом авторов в решение проблемы прогнозирования природных опасностей геофизического происхождения на туристско-рекреационных территориях. Полученные результаты, основанные на перспективных теоретических построениях и экспериментальной проверке математических моделей сейсмического риска, дают возможность заключить, что выбранное направление научных исследований позволяет еще на шаг приблизиться к пониманию и предупреждению катастрофических «замыслов» природы (подчас связанных с активным влиянием антропогенных факторов), мешающих человеку безопасно заниматься туризмом и рекреационной деятельностью.