Онлайн-тестирование по дисциплине "Математика" в современных реалиях

Вынужденный пандемией переход высших учебных заведений на дистанционное образование повлёк за собой необходимость контролировать освоение дисциплины студентами посредством различных онлайн-технологий. Безусловно одним из самых действенных и прогрессивных методов контроля качества знаний является тестирование. Несмотря на определённые недостатки этой формы контроля [1, 2], на сегодняшний день существует достаточно мало эффективных альтернативных методов. Дисциплина «Математика» в принципе является хорошо тестируемой дисциплиной. Однако, наличие большого количества прикладных математических пакетов ставит под сомнение самостоятельное решение студентом тех или иных заданий. Поэтому перед преподавателями возникла задача в разработке таких тестовых заданий, при которых обу- чающийся мог бы продемонстрировать освоение основных математических понятий, а не умение воспользоваться онлайн-калькулятором, что конечно тоже немаловажно в современных реалиях. Для организации тестирования Университетом была выбрана программная среда Moodle. Соответственно, ответом может являться некоторый набор символов, вводимых студентом с клавиатуры.

В общей классификации тестовых заданий выделяют три основных типа: задания с выбором ответа (как одного, так и нескольких), задания открытой формы, когда студенту необходимо самому вписать правильный ответ, и задания на соответствие [3]. Покажем, как были реализованы задания каждого из этих типов.

Задания с выбором ответа. В качестве примеров, рассмотрим следующие задания.

Таблица. Пример 1. Результатом каких действий является число?

1	( a x b ) • ( c x d )	4	( a + b ) x c
2	( a x b ) + ( c x d )	5	( a + b ) x ( c + d )
3	( a x b ) • c	6	x a +^ c

В ответ запишите номера выбранных действий в порядке возрастания, без запятых, пробелов и других дополнительных символов.

Это тестовое задание носит теоретический характер и достаточно хорошо показывает насколько хорошо студент понимает какой объект получается в результате тех или иных действий над векторами. Особенностью подобного типа заданий является то, что количество правильных ответов может варьироваться от одного до шести, что многократно уменьшает возможность случайного выбора экзаменуемым правильного ответа по сравнению с единственным возможным правильным ответом. Очевидно, что онлайн-калькулятор также не может помочь с решением данного вопроса.

Рассмотрим также пример на понятие несобственного интеграла второго рода.

Пример 2. Из перечисленных интегралов выберите несобственные интегралы второго рода.

1^

1) J

dx

3 x - 6

2) J

dx

3 x - 6

3)    J

-^

dx

3 x - 6

4)    J

dx

3 x - 6

³ dx

^J 3 x - 6

В ответе укажите номера выбранных интегралов без пробелов, запятых и других дополнительных символов в порядке возрастания.

И тот и другой пример также удобны для клонирования тем, что при одинаковых исходных данных могут быть поставлены различные вопросы. В первом случае можно попросить выбрать действия, результатом которых является вектор, во втором выбрать несобственные интегралы первого рода.

Рассмотрим теперь задания с открытым ответом. Для того, чтобы исключить онлайн-калькулятор нами использовались задания со своеобразными параметрами.

Пример 3. Произведение матриц размерностей [2 x k ] и [2 m x 4] равно матрице размерности [2 x k ] . Найдите k + m .

Пример отлично показывает насколько студенты усвоили общее понятие умножения матриц, а также умение логически мыслить. Аналогичная мысль прослеживается и в следующем примере на знание табличных интегралов.

Пример 4.

Дано равенство:

Г (   1    . L 1     _x . 1        „

—:---- + cos kx dx = a arete —+ —sin kx + C .

J ( x ² + a ²          J 2       a 4

Найдите a + k .

Обратимся теперь к заданиям на соответствие. Характерной особенностью является то, что в предлагаемых нами заданиях предлагаемые для соответствия объ- екты используются не в полном объёме, а значит студенту необходимо исключить посторонние.

Пример 5. Установите соответствие между функциями и гармониками, которые содержит её ряд Фурье на соответствующем интервале.

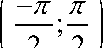
• А)    f ( x ) = x • sin x , ( -n ; n )

• В)    f (x) = x2 - 2x + 3;

1) только cos nx ;             2) только

Б) f(x) = x2 + 3x + 2; (-n;n)

Г) f ( x ) = x (| x | + 1 ) ;

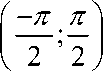
sin nx ;          3) и sin nx , и cos nx ;

4) только cos 2 nx ;     5) только sin 2 nx ;  6) и sin 2 nx , и cos 2 nx .

А	Б	В	Г

В ответе запишите номера правильных ответов в порядке их появления без запятых, пробелов и других дополнительных символов.

Безусловно, нельзя ограничивать контроль знаний студентов только тестированием. Должно быть разумное сочетание методов с тем, чтобы студент продемонстрировал не только знание общих понятий, но и показал вычислительные навыки, а также умение изложить грамотно математически те или иные положения. Контрольная работа, коллоквиум, расчётнографические работы по-прежнему должны оставаться в арсенале преподавателя, но и разумное применение онлайн-тестов как экспресс-метод вполне имеет право на су- ществование.

Окончание пандемии не поставит точку в применении онлайн-тестирования. Си- стема тестирования отлично подходит для текущего контроля знаний и не требует от преподавателя больших временных затрат на проверку студенческих работ, тем не менее позволяя корректировать выбранную стратегию обучения на основе полученных данных. Приведённые в статье тестовые задания апробированы кафедрой «Математика и математическое моделирование» ЮРГПУ(НПИ) им. М.И. Платова на студентах технической направленности и показали свою высокую эффективность. Всевозрастающая мобильность в современном мире, а также приобретённый опыт онлайн-обучения, показывает, что можно организовать качественное обучение применяя современные цифровые тех- нологии, а значит система контроля каче ства знаний также должна продолжать со вершенствоваться.