Оптимизация режимов приготовления теста с использованием муки композитного состава

Автор: Мусаева С. Д., Иманбаев А. Ж., Искакова Ж. А.

Журнал: Вестник Алматинского технологического университета @vestnik-atu

Рубрика: Технология пищевой и перерабатывающей промышленности

Статья в выпуске: 3 (137), 2022 года.

Бесплатный доступ

Разработана математическая модель процесса приготовления теста с применением композитной смеси из овсяной и пшеничной муки I сорта с целью определения оптимальных параметров конечного продукта. В качестве критерия оптимизации приняты органолептические показатели и пищевая ценность хлеба. Входными факторами являлись: влажность теста WT, количество вносимой овсяной муки NМ и кислотность теста КТ.

Овсяная мука, математическое моделирование, оптимизация режимов, пищевая ценность

Короткий адрес: https://sciup.org/140295369

IDR: 140295369 | DOI: 10.48184/2304-568X-2022-3-81-87

Текст научной статьи Оптимизация режимов приготовления теста с использованием муки композитного состава

Анализ научно-технической литературы и основных тенденций развития хлебопекарной промышленности показал перспективность и актуальность комплексного использования сырьевых ресурсов, необходимость создания новых видов сырья. Особое значение при аналитическом проектировании новых видов продуктов отводится показателям пищевой, энергетической и биологической ценности, по которым определяется степень соответствия продукта физиологическим нормам потребности организма [1,2].

Формирование оптимального состава композитной смеси из овсяной и пшеничной муки I-сорта для приготовления хлеба с высокой пищевой ценностью и качества, как правило, связано с необходимостью нахождения некоторой совокупности значений, влияющих факторов, при которых параметр оптимизации принимает экстремальное значение. Во многих случаях практики исследования зависимость параметра оптимизации от технологических параметров (входных факторов) неизвестна и настолько сложна, что аналитическое исследование ее вызывает трудности. В подобных случаях используют математическую теорию планирования экспериментов, которая позволяет найти область оптимальных параметров при постановке наименьшего количества экспериментов.

Материалы и методы исследований

В работе применяли метод ротата-бельного планирования второго порядка (план Бокса).

Результаты и их обсуждение

Чтобы определить наилучшие режимы приготовления хлеба и оптимальные параметры конечного продукта, обычно пользуются критериями оптимизации.

В качестве критерия оптимизации нами приняты следующие показатели хлеба: качественный - объем; пищевая ценносить -содержание железа и йода.

Процесс приготовления хлеба определяется несколькими технологическими параметрами (входными факторами), к числу которых относятся: влажность теста Wt, количество вносимой овсяной муки Nm и кислотность теста Кт.

Существует несколько методов математического планирования эксперимента, среди которых наиболее удобным для описания технологической модели приготовления хлеба с достаточной степенью точности, является ро-татабельное планирование второго порядка.

Таблица 1. Интервалы и уровни варьирования входных факторов в экспериментах с применением овсяной муки

Факторы		Уровни варьирования					Интервал варьирования
Натуральные	Кодированные	-1,682	-1	0	+1	+1,682	0
Влажность теста, Wt %	Хі	39,7	40,4	41,4	42,4	42,7	1
Количество овсяной муки, Nm %	Х2	13,2	20	30	40	46,8	10
Кислотность теста, Кт град.	Хз	2,7	3	3,5	4	4,3	0,5

В связи с этим в дальнейшем рассматривается ротатабельный план второго порядка (план Бокса) при К=3, позволяющий получить оптимальную совокупность входных факторов, влияющих на процесс приготовле- ния хлеба, при которых критерий принимает экстремальное значение.

Интервалы и уровни варьирования входных факторов представлены в таблице-1, а результаты опытов отражены в матрице планирования, которые представлены в таблице-2.

Таблица 2. Матрица планирования и результаты эксперимента

№	Матрица планирования			Объем хлеба
№	Х1	Х2	Х3	У	Ур	(У- У' )	I ү У о} ^_ У о
1	+1	+ 1	+1	965	966,43	2,04
2	+1	+ 1	-1	980	982,99	8,93
3	+1	-1	+1	1145	1174,30	858,72
4	+1	-1	-1	1155	1168,36	178,63
5	-1	+ 1	+1	905	907,80	7,85
6	-1	+ 1	-1	965	951,86	172,56
7	-1	-1	+1	1130	1143,18	173,69
8	-1	-1	-1	1150	1164,74	217,28
9	-1,682	0	0	1075,00	1069,04	35,47
10	+1,682	0	0	1145,00	1121,33	560,11
11	0	-1,682	0	1200,00	1162,37	1415,76
12	0	+1,682	0	800,00	808,94	79,93
13	0	0	-1,682	1125,00	1118,67	40,09
14	0	0	+1,682	1110,00	1086,64	545,44
15	0	0	0	1125	1120,10	23,97	44,44
16	0	0	0	1115	1120,10	26,05	11,11
17	0	0	0	1120	1120,10	0,01	2,78
18	0	0	0	1100	1120,10	404,17	336,11
19	0	0	0	1125	1120,10	23,97	44,44
20	0	0	0	1125	1120,10	23,97	44,44
X				21560		4798,66	483,33

Гипотезу об адекватности модели проверяем с помощью критерия Фишера. В таблице 3 предоставлены значения доверительных интегралов. Получены расчетные зна- чения критерия Фишера Брасч; число степеней свободы для большей 5 и меньшей 5 дисперсий. Зная значения дисперсии, находим таб- личное значение критерия Фишера для дове-ригельной вероятности 0,95% Ртабл=9,01.

Таблица 3. Значения доверительных интервалов

Вид муки	Выходные параметры процесса	Доверительный интервал
Вид муки	Выходные параметры процесса	Abo	Abi	Abii	Abij
Овсяная	Уз	3,27	1,44	1,36	2,46

Таким образом, учитывая, что Ррасч<Ртабл математическая модель технологии хлеба с использованием овсяной муки можно считать адекватной с 95% доверительной вероятностью.

Как известно, коэффициент уравнения регрессии является значимым, если его абсолютная величина больше доверительного интервала (bi>Abi). В противном случае он считается незначимым и может быть исключен из дальнейшего рассмотрения модели [3].

Сравнивая значения доверительных интервалов из таблицы 3 с соответствующи- ми коэффициентами регрессии в таблице 4 можно сделать вывод о том, что эффекты взаимодействия входных факторов незначительны, и можно было бы ими пренебречь. Однако, поскольку нам предстоит осуществить поиск оптимума функций откликов с наибольшей точностью, то следует не исключать незначимых коэффициентов из уравнений регрессии [4]. С учетом сказанного получим следующие уравнения регрессии:

у8=1180+15,56хі-105,19х2-9,53хз+6,87хіх2+6,87хіхз-5,62х2хз- (1))

После раскодирования независимых переменных с (1) получим уравнения регрессии при натуральных значениях факторов:

s=-12275,75+677,75Wt-6,46Nm-381,47Kt+0,69WtNm+13,75WtKt-1,12NmKt-

-8,83Wt2-0,48Nm2-24,73Kt2 . (2))

Таблица 4. Коэффициенты уравнений регрессии выходных параметров

Коэффициенты	Овсяная мука
Коэффициенты	уі
при кодированных значениях факторов		при натуральных значениях факторов
bo	1120,10397	Во	-12275,7476
bi	15,56232	Bi	677,7471
b2	-105,188	В2	-6,46241
Ьз	-9,53064	Вз	-381,473
Ьі2	6,875	Bi2	0,6875
Ьіз	6,875	Віз	13,75
b23	-5,625	В 23	-1,12500
bii	-8,82772	Bii	-8,82772
b22	-1,76357	В 22	-0,47636
Ь зз	-6,18172	Взз	-24,7269
Расчетное значение критерия Фишера Брасч
FrARn=9.01	1 8 93

Изучение объекта исследования проводили при помощи графического метода (изучение поверхности отклика с помощью двухмерных сечений), позволяющего получить наглядное представление о закономер ностях изменения критериев при варьирова нии факторов. Для этого необходимо полученное адекватное уравнение второго поряд- ка по плану Бокса преобразовать в уравнение канонического вида [3,4]:

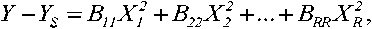
Следовательно, чтобы построить отклики двухмерных сечений для изучения закономерности критериев при варьировании факторов необходимо определить систему координат точки и значения критерия оптимизации в новом центре У ^ .

После канонического преобразования моделей второго порядка были получены уравнения регрессии в канонической форме, параметры которых, вычисленные на ЭВМ и необходимые для графического анализа поверхно- стей отклика методом двухмерных сечений для внесения овсяной муки, приведены в таблице 5.

Как видно, коэффициенты канонических уравнений имеют одинаковые знаки. Следовательно, поверхности отклика во всех парных сочетаниях факторов будут иметь эллиптическую форму. Уравнение (3) использовали для построения линии равных значений отклика, которые имели вид эллипса.

Таблица 5. Параметры, характеризующие поверхности отклика

Номера факторов	Координаты центра поверхности	Центр оптимума	Угол поворота осей координат	Коэффициенты регрессии в канонической форме
1-2	Хі=0,46 Х2=-0,17	уs=1180	т=5°	В:-1=-8,53 В2-2=-1,79
1-3	Хі=0,74 Хэ=-0,36	уs=1177	т=-34,5°	Вх-1=-11,19 Вэ-э=-3,82
2-3	Х2=-0,19 Хэ=-0,28	уs=1179	т=3,9°	В2-2=-1,78 Вэ-э=-5,99

Анализ двухмерных сечений (рис. 2) показывает, что необходимые значения критериев ys, удовлетворяющие требования, предъявляемые к объему хлеба, достигаются в рассматриваемой области поиска. Это означает, что уровни варьирования входных факторов при планировании экспериментов были приняты достаточно правильно.

у = Основнойіп(х) - Основной R2= Основной

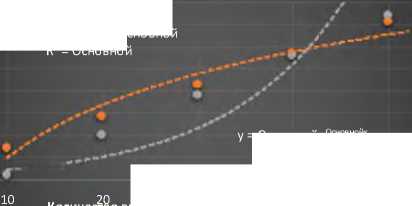
= ОсновнойеОсновнойх

R2 = Основной

30 40

Количество-вносимои овсяной муки, % Й д Запад

Рисунок-1. График зависимости содержания Fe и J в 100 г готового изделия от количества внесенной овсяной муки

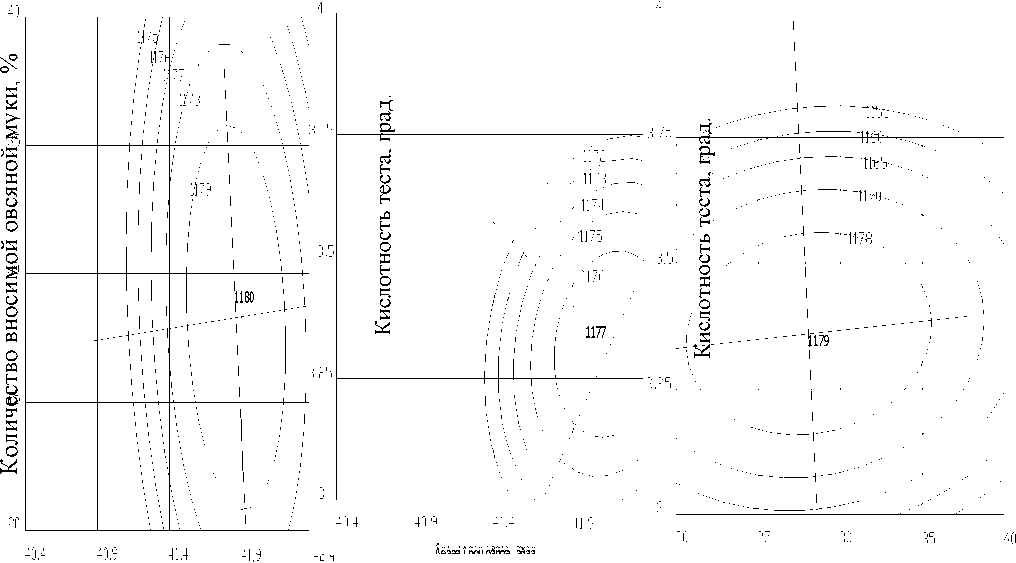
Влажность теста, %

Количество овсяной муки, %

Рисунок-2. Двухмерные сечения для изучения влияния входных факторов на показатель объема хлеба приготовленного на основе муки композитного состава из овсяной пшеничной 1-сорта.

а - Хі и Х 2 при Хз=0;
б - Хі и Хз при Х 2 = 0 ;
в - Х 2 и Хз при Хі=0

Заключение, выводы

В результате реализации оптимизационной модели получены следующие оптимальные режимы замеса теста с использованием овсяной муки:

- влажность теста Wt = 41,9 %
- количество вносимой овсяной муки N m = 27,5 %
- кислотность теста К т = 3,4 град

Таким образом, полученные результаты математического моделирования технологического процесса замеса теста с использованием овсяной муки в пшеничном хлебе, позволили научно обосновать оптимальные режимы приготовления хлеба с высоким содержанием минеральных веществ: Fe=20,4

мг, J=481,6 мкг и удельным убъемом-1180 смзз, при которых достигаются наилучшие технологические показатели.

Список литературы Оптимизация режимов приготовления теста с использованием муки композитного состава

Абдрахим А. Использование овсяной муки в производстве хлеба / А. Абдрахим, С. Д. Мусаева, Р. А. Изтелиева // Ізденістер, нәтижелер - Исследования, результаты. - 2017. - № 6 (78) - С. 252-257.
Пономарева Е. И. Прогнозирование пищевой ценности хлебобулочных изделий на основе математического моделирования биохимических превращений / Е. И. Пономарева // Вестник ВГУИТ. - 2013.- № 1. - С. 63-67.
Статистические методы анализа данных / Л. И. Ниворожкина; под общ. ред. д. э. н., проф. Л. И. Ниворожкиной. - М.: РИОР: ИНФРА-М, 2016. - 333 с.
Казаков А. В. Планирование эксперимента и измерение физических величин / А. В. Казаков. - Пермь: Пермский национальный исследовательский политехнический университет, 2014. - 89 с.
Перенести в английский вариант.
Abdrahim A., Musayeva S. D., Iztelieva R. A. The use of oat flour in bread production // Izdenister, natizheler - Research, results. - 2017. - No. 6 (78). Pp. 252-257.
E. I.Ponomareva, V. I.Ryazhskikh, V. Yu. Kaveshnikov, N. M. Zastrogina. Forecasting the nutritional value of bakery products based on mathematical modeling of biochemical transformations // Vestnik VGUIT. - 2013.- No.1. Pp. 63-67.
Statistical methods of data analysis / L. I. Nivorozhkina, S. V. Arzhenovsky, A. A. Trudyaga; under the general editorship of Doctor of Economics, prof. L. I. Nivorozhkina. - M.: RIOR: INFRA-M, 2016. - 333 p.
Kazakov A. V. Experiment planning and measurement of physical quantities. - Perm: Perm National Research Polytechnic University, 2014. - 89 p.

Еще

Статья научная