Повышение мотивации к изучению математики у школьников

Требования к результатам освоения образовательной программы основного общего образования определены федеральным государственным стандартом. Выпускник должен быть ориентирован на моральные ценности и нормы, за-мотивирован, уметь ставить цели, дей- ствовать в ситуации неопределенности, иметь активную позицию в своем обучении и развитии, уметь работать с информацией, проводить исследовательскую работу, оценивать результаты своих действий и риски. В процессе обучения школьник должен научиться работать са- мостоятельно и в группе, быть готовым к разнообразной совместной деятельности, действовать на принципах взаимопонимании, взаимопомощи и уважении, уметь донести свою точку зрения, получать новые знания от учителей и других обучающихся.

Перечисленные требования ФГОС невозможно реализовать без регулярного обеспечения специальных условий проведения уроков и без формирования устойчивой мотивации каждого обучающегося. В данной статье рассмотрим возможность обеспечения этих позиций в образовательном процессе.

Вопросы формирования мотивации у обучающихся в своих работах освещали Л.И. Божович, Г.Г. Зайцев, Е.П. Ильин, И.В. Калинина, А.Н. Леонтьев, Л.В. Мамедова, М.Е. Королёва, С.А. Пугина, Э.А. Уткин, Г.П. Щедровицкий, М.В. Юра-кова и др.

Понятие мотивации и подходы к формированию мотивации рассмотрены достаточно широко. Существуют различные подходы к определению понятия мотивации. Л. И. Божович и Г.Г. Зайцев определили мотивацию через понятие побуждения, которое возникает из личностных характеристик и ценностей [1, 3]. Е.П. Ильин рассматривает мотивацию как динамический процесс формирования мотива – объективной ценности результата [4]. Мотивацию как состояние личности, определяющее направление деятельности человека, понимает Э.А. Уткин [11]. М.В. Юракова мотивацию к изучению математики определяет как «совокупность причин, связанных с математическим содержанием и индивидуальным опытом обучающихся, побуждающих к возникновению математических действий, выбору направленности и способов осуществления математических действий» [13].

Подходы к формированию мотивации к учебной деятельности достаточно разнообразны. С.А. Пугина рассматривает содержательный аспект способов формирования мотивации на различных этапах урока через осознанность обучающимися положительного опыта изучения материала на уроке геометрии [10]. Л.В. Мамедова, М.Е. Королёва отмечают проблему сохранения мотивации к обучению обучающихся при переходе в пятый класс [8]. И.В. Калинина выделяет в качестве основных способов воздействия на повышение мотивации у школьников содержательный, игровой, использование современных компьютерных технологий [5]. В работе М.В. Юраковой перечислены популярные педагогические приемы повышения мотивации к учебе: демонстрация актуальности данных, создание условий для установления связи задачи с личным опытом обучающихся [13]. В качестве мотивирующего способа М.В. Юракова предлагает использование мотивационных заданий с наличием математического содержания, связи задачи с опытом обучающихся.

Среди видов побуждений к учебной деятельности наиболее популярными являются:

– создание проблемной практической ситуации, в ходе которой формируется потребность в получении новых знаний и опыта;

– понятность и наглядность изложения материала;

– включение исторических справок и материалов;

– решение нестандартных задач и задач различной степени сложности;

– использование интересных методик обучения, в том числе проведение игр, опытов и проектов;

– использование современных информационных технологий;

– прозрачность и понятность всех действий, операций и результатов поставленных учебных задач.

Таким образом, мотивацию понимают как основное условие для успешной учебы. Ей отводится даже более существенная роль, чем интеллектуальным характеристикам обучающегося. В большинстве научных исследований отмеча-

Повышение мотивации к изучению математики у школьников

Е.А. Омельченко

ется необходимость введения мотивационных элементов на всех этапах урока и целого процесса обучения.

Безусловно, повышение учебной мотивации обучающихся является одной из первостепенных задач учителя. Отметим, что мотивация определяется в первую очередь личностными ценностями (свобода, здоровье, доброта, честность, стремление к истине, нравственность, гуманизм, сострадание, стремление создать создавать социальное благополучие, сохранение природы, созидание, приобретение знаний) и актуальными потребностями человека. Поэтому формирование мотивации к учению школьников невозможно без учета набора его ценностей и интересов, которые на начальном этапе обучения можно определить в беседе, игре, анкетировании.

Одним из эффективных методов активного обучения считается метод вопросов и ответов, где используются предварительно составленный набор вопросов. Его сравнивают с обычным собеседованием. Этот метод хорошо себя показывает на начальном этапе изучения курса, раздела или темы. Заранее подготовленные вопросы помогут каждому школьнику через личную ценностно шкалу выстроить список своих потребностей (целей), мотивирующих на изучение материала.

Приведем несколько примеров таких вопросов:

– Какие качества ты ценишь в человеке?

– Какие качества позволяют человеку добиться значимых результатов в своей жизни?

– Какие действия надо предпринимать, чтобы воспитать в себе эти качества?

– Какую роль играет изучение математики в формировании личности человека?

– Какие темы в этой четверти ты считаешь наиболее важными для изучения, а какие менее важными?

– Можно ли сделать процесс обучения математики более полезным?

– Можно ли сделать процесс обучения математики более быстрым?

– Можно ли сделать процесс обучения математики более легким?

– Можно ли сделать процесс обучения математики более интересным?

Чтобы обеспечить отсутствие дискомфорта учеников, честность и полноту ответов, можно обеспечить их анонимность, например, оформить письменно или напечатать в электронном виде заранее. В процессе обсуждения всех ответов обучающиеся самостоятельно делают выводы о важности изучения математики лично для них, о выборе дополнительных тем для изучения (помимо обязательных тем), способов обучения, выстраивания своего графика обучения, расставляя приоритеты с учетом личных потребностей, что повышает интерес к изучению темы.

С помощью данного метода фокус школьников переносится с текущих интересов, например, поиграть в телефоне, на главные жизненные цели. Расставляются приоритеты таким образом, чтобы обучение стало более комфортным и интересным. Однако метод собеседования предполагает использование заранее заготовленных вопросов, что, с одной стороны, дает пример процесса вопрошания и возможность привыкнуть к такого рода работе, с другой стороны, оставляет отвечающего в более пассивной роли и не дает в полной мере раскрыть и учесть все особенности его личности и опыта.

В своих работах В.Л. Данилова, В.Е. Карастелев [2, 6] изучают и описывают более эффективную, на наш взгляд, технику вопрошания как умение обучающихся самим формулировать вопросы, помогающие решать поставленные задачи. Умение задавать вопросы является эффективным инструментом познания и свершения открытий. Техника имеет широкую сферу применения, основывается на многолетнем опыте решения креатив- ных, управленческих, исследовательских задач.

В рамках школьной программы применение этой техники представляет большой интерес. Так как она исключает пассивную позицию при изучении материала, предполагает как индивидуальную работу обучающихся, так и групповую, заключается в формировании умения обучающегося задавать вопросы, тем самым делать его ключевым организатором своего пути развития. Для реализации такой техники следует придерживаться простых принципов:

– объявить фокус вопросов;

– на первоначальном этапе не отвечать и не комментировать на вопросы;

– нет плохих и неправильных вопросов;

– количество вопросов не ограничено.

После формирования наборов вопросов по теме обучающимся может быть предложено классифицировать вопросы, составить из них иерархическую структуру, начертить схему или дерево вопросов. Таким образом формируется перечень вопросов для глубокого изучения темы, учитывающий все интересы и увлечения участников, отвечающий на их интеллектуальные запросы. Учитывая, что авторами вопросов являются обучающиеся, то можно с уверенностью сказать, что все пункты изучаемой проблемы уже связаны заинтересованностью через их личностные ценности и потребности, что указывает на высокую мотивацию к глубокому изучению данной темы не только в ее рамках, но и дальнейшего изучения следующих тем.

Заключительным этапом применения метода вопрошания является рефлексия. Помимо изучения темы, обучающиеся могут наблюдать за изменением своих вопросов, их качеством, проанализировать свой выбор вопросов, определить их приоритетность и выбрать перечень вопросов, на которые будут искать ответы.

Нами был проведён эксперимент по повышению уровня мотивации среди обучающихся шестых классов на уроках математики с применением техник задавания вопросов.

На подготовительном этапе в начале четверти школьникам в качестве домашнего задания предложен список первых четырех вопросов, представленный выше, на которые нужно было ответить. Ответы оформлены анонимно на небольших листочках. На уроке дети, работая в небольших группах, сгруппировали ответы, проанализировали их, сделали выводы и поделились ими с остальными. Таким образом, у всех сложилась полноценная картина о ценностях и интересах класса. Второе задание заключалось в ответе на следующие пять вопросов, представленных выше. Для работы детям предварительно даны темы, которые будут изучаться в этой четверти. Работа выстраивалась так же, как и в первом задании. Стоит отметит вовлеченность детей: при выполнении первого задания наблюдалось настороженность и недоверие, а при выполнении второго задания обучающиеся активно предлагали и обсуждали свои ответы. Сведение всех ответов позволило выстроить общую и индивидуальную стратегию изучения учебного материла с учетом интересов и рекомендаций каждого ученика. Дети с большим интересом, чем обычно, приступили к изучению математики.

Далее на уроках использовался метод формулирования вопросов. На этапе объявления темы предлагается сформулировать вопросы по данной теме, чтобы качественно ее изучить. Вопросы выписываются на доске, из них составляется схема изучения темы. Среди них были такие вопросы: «Что я уже знаю по этой теме?», «Какой имею опыт по теме и чему могу научить?». Обсуждение данных вопросов обеспечило более глубокую мотивацию к изучению темы.

На этапе непосредственного изучения темы появляются такие вопросы, как «Какими ресурсами я могу воспользоваться, чтобы лучше изучить тему урока?», «Что мне было непонятно и как

Повышение мотивации к изучению математики у школьников

понять?», «Где я могу использовать эту информацию в дальнейшем?». Здесь будет уместен вопрос от учителя: «Какие можно задать вопросы ученику, чтобы увериться в понимании им темы урока?», «Чего вам не хватило для максимального понимания темы и отработки навыков?».

На заключительном этапе урока дети задаются вопросами не только о том, чем полезен был урок, чему новому научились, но и каким способом могли бы они рассказать об этой теме, как могли бы представить данную тему наглядно, какое бы домашнее задание они себе придумали и в какое бы направление углубились при изучении данной темы.

В ходе исследования были определены две группы обучающихся. В пер- вой (контрольной) группе реализовывались прежние методы обучения, во второй (экспериментальной) – методы формулирования вопросов. В качестве показателей эффективности метода принята успеваемость школьников по математике. Качественная успеваемость до начала эксперимента составляла 77,3% в экспериментальной группе и 63,6% в контрольной. В экспериментальной группе отличников 40,9%, обучающихся на «4» и «5» 36,4 % и с базовой успеваемостью 22,7%. В контрольной группе отличников 22,7%, обучающихся на «4» и «5» 40,9 % и с базовой успеваемостью 36,4%. Анализ успеваемости за отчетный период представлен в табл. 1 и рис. 1.

Таблица 1 – Входные результаты

Уровень успеваемости	Экспериментальная группа, %	Контрольная группа, %
высокий	40,9	22,7
повышенный	36,4	40,9
базовый	22,7	36,4
ниже базового	0	0
Качественная успеваемость	77,3	63,6
Абсолютная успеваемость	100	100

100 100

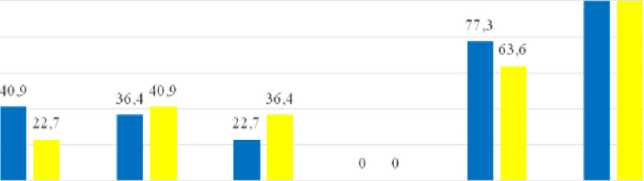
высокий уровень повышенный базовыйуровень уровеньусп Качественная Абсолютная усп уровеньусп. усп. ниже базового успеваемость успеваемость

• ■ Экспериментальная группа    Контрольная группа

Рисунок 1 – Входные результаты

Е.А. Омельченко

Качественная успеваемость до начала эксперимента составляла 90,9% в экспериментальной группе и 59,1% в контрольной. В экспериментальной группе отличников и обучающихся на «4» и «5» по 45,5% и с базовой успеваемостью

• 9,1 %. В контрольной группе отличников 18,2%, обучающихся на «4» и «5» и с базовой успеваемостью по 40,9%. Анализ успеваемости за период применения метода вопросов представлен в табл. 2 и рис. 2.

Таблица 2 – Итоговые результаты

Уровень успеваемости	Экспериментальная группа, %	Контрольная группа, %
высокий	45,5	18,2
повышенный	45,5	40,9
базовый	9,1	40,9
ниже базового	0	0
Качественная успеваемость	90,9	59,1
Абсолютная успеваемость	100	100

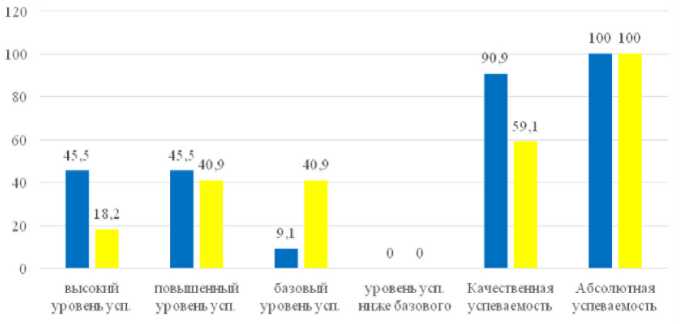
■ Экспериментальна я группа    К онтр ольная группа

Рисунок 2 – Итоговые результаты

Таким образом, качественная успеваемость в экспериментальной группе выросла на 13,6% и в контрольной группе уменьшилась на 4,5%. В экспериментальной группе количество обучающихся с высоким уровнем успеваемости увеличилось на 4,6%, с повышенным уровнем успеваемости повысилось на 9,1% и с базовой успеваемостью снизилось на 13,6%. В контрольной группе количество обучающихся с высоким уровнем снизилось на 4,5%, с повышенным уровнем успеваемости – не изменилось, с базовой успеваемостью увеличилось на 4,5%. Все изменения представлены в табл. 3-5 и рис. 3-5.

Таблица 3 – Сравнительные результаты экспериментальной группы

Экспериментальная группа	Входные результаты, %	Итоговые результаты, %
высокий уровень успеваемости	40,9	45,5
повышенный уровень успеваемости	36,4	45,5
базовый уровень успеваемости	22,7	9,1
уровень успеваемости ниже базового	0	0
Качественная успеваемость	77,3	90,9
Абсолютная успеваемость	100	100

Повышение мотивации к изучению математики у школьников

100 100

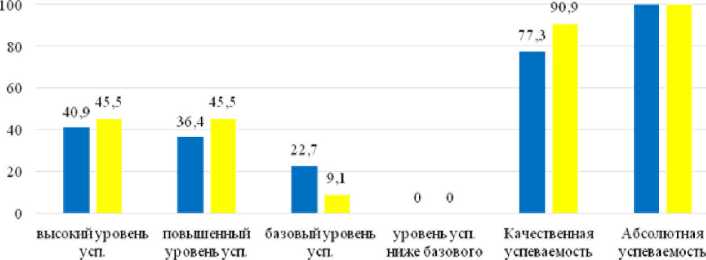
■ Входныерсз Итоговыерез

Рисунок 3 – Качественные изменения результатов экспериментальной группы

Таблица 4 – Сравнительные результаты контрольной группы

Контрольная группа	Входные результаты, %	Итоговые результаты, %
высокий уровень усп.	22,7	18,2
повышенный уровень усп.	40,9	40,9
базовый уровень усп.	36,4	40,9
уровень усп. ниже базового	0	0
Качественная успеваемость	63,6	59,1
Абсолютная успеваемость	100	100

100 100

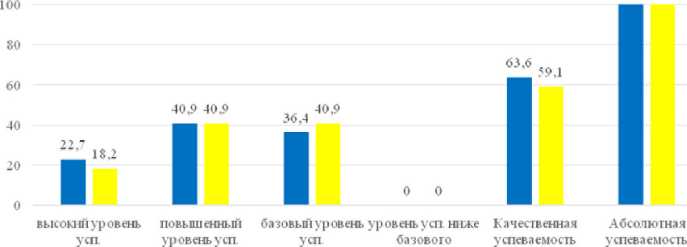
■ Входныерез Итоговыерез

Рисунок 4 – Качественные изменения результатов контрольной группы

Таблица 5 – Сводные результаты изменения качественной успеваемости

Уровень успеваемости	Экспериментальная группа, %	Контрольная группа, %
высокий	4,6	-4,5
повышенный	9,1	0
базовый	-13,6	4,5
ниже базового	0	0
Качественная успеваемость	13,6	-4,5
Абсолютная успеваемость	0	0

■♦■'Пзменнення результатов контр спьной группы

Рисунок 5 – Качественные изменения результатов групп

Из приведённых расчетов видно, что данный подход к обучению показал себя достаточно эффективным. Практически на каждом уроке есть возможность формировать достаточно большой спектр личностных, предметных, мета-предметных результатов освоения образовательных программ ФГОС, грамотно формировать у детей ценность научного познания, межличностного общения, гражданственности и культуры. Несмотря на различные личностные психологические характеристики, уровень знаний обучающиеся в равной степени включаются и проводят сложную аналитическую работу. При этом творческий и интеллектуальный вклад и значимость каждого школьника для общего дела очевиден на протяжении всего урока, что подкрепляет самооценку и веры в свои силы. Дети становятся более раскрепощенными, заинтересованными, учатся высказываться, принимать другие точки зрения, мыслить критически. Уровень мотивированности детей к изучению математики при таком подходе стал более высоким, что отмечают и сами дети.

Полученный навык формулирования вопросов в дальнейшем помогает самостоятельно быстро и качественно разобраться в любой теме и ситуации, составлять качественные тексты, проводить исследовательскую работу, находить неординарные решения любых задач в учебе, на производстве, строить траекторию своего развития.