Системно-комплексная диагностика качества математического образования в общеобразовательных организациях

потенциала общеобразовательной организации. Можно утверждать, что каждой общеобразовательной организации присуща своя модель математического образования. Актуальность проблемы оценки качества математического образования, реализуемого в общеобразовательных организациях, обусловлена необходимостью оптимальной организации учебного процесса обучения математике с целью его постоянного совершенствования с учетом социально-экономических ситуаций и педагогических реалий.

Проблеме оценки качества математического образования как одной из самых актуальных для всей системы российского образования посвящено много работ. Оценка качества математического образования в последнее время проводится в основном на базе рейтинга, включающего показатели учебных достижений выпускников по конечному результату (массовое тестирование учащихся общеобразовательных организаций по математике в формате ГИА). По показателям учебных достижений выпускников определяется рейтинг общеобразовательных организаций в областном, региональном и во всероссийском масштабе. С.Ю. Сергеева, Е.Д. Обревко предлагают оценивать качество образования на основе процессного подхода с учетом трех групп критериев: качества результата образовательного процесса, качества условий осуществления образовательного процесса, качества реализации образовательного процесса [12]. В.А. Ясвин, С.Н. Рыбинская, С.А. Белова, С.Е. Дробнов предлагают оценивать качество образования в школах на основе комплексного рейтинга, включающего показатели предметных образовательных результатов обучающихся и показатели образовательных условий и личностно-развивающих возможностей самих школ [14]. Большой интерес в последнее время вызывает метод рангового анализа в технологии оценки и контроля качества образования в образовательных учреждениях, который представлен в работах Р.В. Гуриной и В.В. Бедаш [3]. К сожалению, предлагаемые контрольно-оценочные системы не является унифицированными и всеобъемлющими, т. к. в основном опираются на анализ различных диаграмм, таблиц, а также текстовых описаний отдельных параметров исследуемых объектов. Несмотря на продуктивность и инновационные находки ученых, методистов, практиков, проблема оценки качества математического образования в школах тем не менее по-прежнему остается актуальной.

В данной статье описана методика оценки качества математического образования в общеобразовательных организациях на основе системно-комплексной диагностики. Системно-комплексная диагностика представляет собой синтез системного и комплексного исследования изучаемого объекта, реализуемого в наши дни с помощью компьютерных технологий и математических (количественных) методов. Системное исследование объекта предполагает его изучение как целостной системы, дифференцированной на взаимодействующие элементы. Комплексное исследование позволяет выявить сущность явлений и процессов в многообразных структурных составляющих сложных объектов в аспекте их привязанности ко времени и месту. Системнокомплексное изучение исследуемого объекта как единого целого с позиций системного анализа, взаимосвязи, изучения отдельных структурных частей и выявления роли каждой из них в общем функционировании системы позволяет дать качественную интерпретацию причинно-следственных связей целостных явлений. Таким образом, под системнокомплексной диагностикой качества математического образования в общеобразовательной организации понимается комплекс научно обоснованных процедур, который позволяет выявить характер изменений в образовательной системе обучения математике за определенный период с целью прогностического слежения за его состоянием.

Наряду с понятием «диагностика» в научной литературе широко используются такие понятия, как «мониторинг», «оценка». Рассмотрим их взаимосвязь.

Под мониторингом понимается специально организованное, систематическое наблюдение за состоянием педагогических систем, предполагающее сбор, обобщение, анализ информации с целью слежения за их состоянием и прогнозирования их дальнейшего развития [6; 9]. Комплексность сведений об объекте наблюдения (набор индикаторов, разносторонне отражающих состояние, и факторы, влияющие на развитие объекта) считается важнейшей отличительной характеристикой этого метода исследования, позволяющего принимать управленческие решения с учетом различных факторов. Под диагностикой понимается процесс / деятельность, заключающаяся в изучении и оценивании фактического состояния и особенностей объектов. Отличие диагностики от мониторинга заключается в том, что диагностика является одним из инструментов комплекса процедур мониторинга. Оценка (оценивание) в педагогике – это условно-формальное (знаковое), количественное выраже- ние диагностики состояния педагогической системы в цифрах, буквах или иным образом, отражающее социальные требования к качеству педагогической системы [4; 11].

Механизмом системно-комплексной диагностики качества математического образования в общеобразовательных организациях является контроль за деятельностью такой системы, как математическое образование в общеобразовательной организации, который выражается как во внутрисистемной, так во внесистемной аналитике и представляет собой сбор данных об условиях реализации образовательных программ, результаты промежуточной и итоговой аттестации, оценка квалификации учителей математики, мониторинг внеучеб-ных достижений всех субъектов математического образования в конкурсных мероприятиях (олимпиады, смотры, конкурсные мероприятия, публичные доклады) в системе образования и т. д.

Основой системно-комплексной диагностики оценки качества математического образования в общеобразовательных организациях является методика «свертки качеств», предложенная А.Н. Колмогоровым [7]. В основу методики «свертки качеств» положены следующие идеи: а) эффективность системы оценивается по комплексу различных критериев, образующих систему со сложной иерархической структурой [1]; б) общее качество всей системы формируется из определенных частных оценок качеств по уровням иерархии системы, которые сворачиваются в единый критерий в соответствии со средней функцией переменных Колмогорова – Нагумо [7]. Под средней функцией переменных Колмогорова – Нагумо понимается функция, значения которой всегда принадлежат интервалу, занимаемому конкретным набором значений аргументов. Введение нормального интервала задает единый масштаб для всех частных качеств, а использование средних функций приводит к тому, что единое качество выражается в этом масштабе. Данная методика успешно используется для оценки качества и оптимизации различных сложных объектов в механике, химической технологии, экономике и педагогике высшей школы [15; 16]. Данная методика позволяет дать оценку качества математического образования в общеобразовательных организациях, определить проблемное поле и направления для совершенствования математического образования.

Разработка критериально-диагностического инструментария для оценки качества математического образования в общеобразователь- ных организациях является довольно сложной задачей, поскольку объектом диагностирования выступает сложная образовательная система – математическое образование в общеобразовательной организации. За основу выявления критериев для системно-комплексной диагностики математического образования в общеобразовательной организации мы выбрали один из подходов к определению качества образования, согласно которому в критериях качества образования выделяют четыре направления:

• –    соответствие цели (определенного уровня знаний и умений, умственного, физического и нравственного развития выпускников образовательной организации) и результата как меры достижения цели;

• –    содержание математического образования, обеспечивающее целостность развития личности обучающегося;

• –    особенности учебного процесса, соответствующие современным требованиям наук, в особенности философии, психологии, педагогики и методики обучения математике;

• –    создание в общеобразовательной организации таких условий, которые оптимальны для реализации целей математического образования [2, с. 28].

В соответствии с четырьмя направлениями оценки качества математического образования в общеобразовательной организации были определены критерии. Выделенные критерии в определенной степени связаны друг с другом, могут иметь свой низкий или высокий показатель, что отражается на интегральной оценке качества математического образования в общеобразовательных организациях. Соответственно четырем критериям качества математического образования в общеобразовательных организациях были определены показатели, оцениваемые по 5-балльной шкале целыми цифрами от 0 до 4. Более наглядно критерии и соответствующие им показатели с диапазоном возможных значений представлены в табл. 1.

Формирование единого критерия качества производится на основе анализа взаимоотношений частных качеств, выраженных в форме графа-иерархии (рис. 1). Возможность количественного выражения взаимоотношений частных качеств и единого качества основывается на двух предварительных условиях:

• 1)    общая шкала для всех групповых и единого качества нормирована (интервал [0, 1]);

• 2)    для формирования единого критерия качества используются средние функции.

Системно-комплексная диагностика качества математического образования в общеобра-

Таблица 1

	Критерии и показатели	Диапазон измерения
Q 1	Научно-целевой (характеризует соответствие целей математического образования в общеобразовательной организации требованиям общества и времени)	0–16
q11	Наличие целевого ориентира, соответствующего требованиям общества и времени и реализуемого каждым субъектом математического образования в общеобразовательной организации	0–4
q12	Согласованность (соответствие) целевых ориентиров, мотивов всех субъектов математического образования в общеобразовательной организации	0–4
q13	Наличие нормативно-правовой основы и концептуальной основы, что предполагает подготовку и наличие всех необходимых документов для организации математического образования как инновационной образовательной системы в общеобразовательной организации	0–4
q14	Включенность педагогов на уровне команды единомышленников в проектирование и реализацию математического образования в общеобразовательной организации как инновационной образовательной системы	0–4
Q 2	Деятельностно-организационный (характеризует интеграцию методологий, методов, технологий обучения, моделей деятельности, обусловленной личностной направленностью математического образования в общеобразовательной организации) с учетом тенденций развития математического образования	0–16
q21	Полнота и целостное единство компонентов математического образования как инновационной образовательной системы, реализуемой в общеобразовательной организации	0–4
q22	Взаимообусловленность процессов интеграции и дифференциации при реализации математического образования в общеобразовательной организации как инновационной образовательной системы	0–4
q23	Отбор соответствующего содержания, отбор технологий, методов обучения с учетом тенденций развития математического образования, осуществление обучения математике на основе традиций и инноваций	0–4
q24	Интерактивность математического образования, его адаптивность и адекватность к изменениям, происходящим в обществе (функциональная возможность математического образования в общеобразовательной организации, позволяющая его субъектам гибко реагировать на запросы социума)	0–4
Q 3	Содержательно-качественный критерий (характеризует направленность обучения математике на целостность развития личности обучающегося средствами математики, а также практикоориентированную направленность обучения математике, позволяющую после окончания общеобразовательной организации успешно самореализоваться в социуме)	0–16
q31	Многообразие, вариативность компонентов математического образования в общеобразовательной организации как инновационной образовательной системы, позволяющих выстраивать разнообразные образовательные траектории обучающихся с учетом потенциальных возможностей и познавательных интересов обучающихся	0–4
q32	Конструирование (агрегирование) элементов математического образования в общеобразовательной организации как инновационной образовательной системы обучения математике с учетом развития математического образования, обусловленного социально-экономической ситуацией (ориентированных на развитие метапредметных умений и навыков обучающихся)	0–4
q33	Саморазвитие и самоорганизация субъектов математического образования в общеобразовательной организации (результативность обучения математике в рейтинговых показателях)	0–4
q34	Школьный менеджмент и качество управления	0–4
Q 4	Качественно-пространственный критерий (характеризует обеспечение оптимальных условий организации математического образования в общеобразовательной организации)	0–16
q41	Создание благоприятного эмоционально положительного микроклимата, здоровьесберегающих условий для всех субъектов математического образования в общеобразовательной организации	0–4
q 42	Материально-техническое оснащение математического образования в общеобразовательной организации с учетом тенденций развития математического образования, обусловленных социально-экономической ситуацией, возможность максимального использования субъектами математического образования в общеобразовательной организации его ресурсного обеспечения	0–4
q43	Высокая методологическая подготовка учителей математики; педагогическое партнерство и взаимодействие в реализации математического образования в общеобразовательной организации как инновационной образовательной системы обучения математике	0–4
q44	Степень функционального комфорта и степень вовлеченности в деятельность коллективного субъекта математического образования в общеобразовательной организации	0–4

Критерии и показатели качества математического образования в общеобразовательных организациях

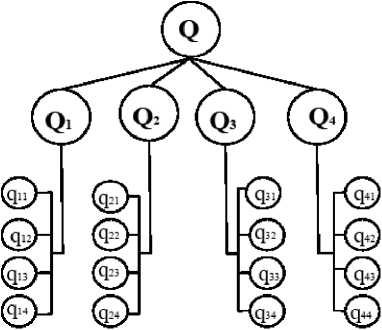
Рис. 1. Иерархическая схема суммарной оценки качества модели математического образования в общеобразовательной организации

Качественная оценка содержательно-качественного критерия:

Q3 := -In

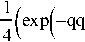
+ ехРНчч32

+ exp(-qq33) + exp(-qq34j)

Качественная оценка качественно-пространственного критерия:

Qq := -In

+ exp(-qq42)

+ exp(-qq43)

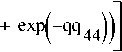
Q – обобщенный показатель качества:

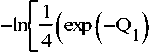
+ exp

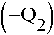
зовательной организации имеет вид четырехуровневой иерархической системы.

Суммарная оценка качества математического образования в общеобразовательной организации определяется качественными оценками четырех интегральных свойств системы: Q – обобщенный показатель качества Q = Q (Q₁, Q₂, Q₃, Q₄), он формируется из следующих критериев: Q₁ – научно-целевой; Q₂ – деятельностно-организационный; Q₃ – содержательно-качественный; Q₄–качественно-про-странственный.

Качество модели математического образования в общеобразовательной организации (интегральное свойство) Q определяется сверткой нормированных критериев качества образовательной системы, которые в свою очередь являются сверткой нормированных показателей (четырехуровневая свертка):

Q1 = Q1 (q11; q12; q13; q14), Q2 = Q2 (q21; q22; q23; q24), Q3 = Q3 (q31; q32; q33; q34), Q4 = Q4 (q41; q42; q43; q44).

Качественная оценка научно-целевого критерия:

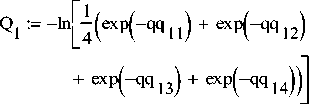
Качественная оценка деятельностно-организационного критерия:

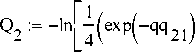
+ ^("^22)

+ ехР(-ОД2з) +

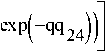
+ exp I— Q3j + exp

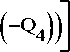
По каждому из выбранных критериев оценивалась чувствительность всей системы как нормированной общей целевой функции по отдельным параметрам. Выбранные параметры обеспечивают приемлемую чувствительность изменения целевой функции при изменении входных параметров системы, что означает, что модель адекватно описывает реальную ситуацию.

Предлагаемая нами системно-комплексная оценка качества математического образования в общеобразовательных организациях реализована в программном пакете VisSim, в котором иерархия системы представлена в виде взаимосвязанных блоков MathCad. Предложенная методика и разработанная на ее основе автоматизированная программа позволяют оперативно по многим показателям провести оценку качества математического образования в общеобразовательных организациях. Данная методика является универсальной, границы ее применимости обусловлены развитием педагогической науки, т. к. она позволяет фиксировать «новое» качество в парадигме новых подходов и требований к нему с учетом новых приоритетов образовательной политики. В дальнейшем представленная системнокомплексная диагностика оценки качества математического образования в общеобразовательных организациях может быть легко расширена путем введения новых параметров системы. Подключение к ней нового блока, производящего оптимизацию целевой функции, позволит находить оптимальные значения параметров исследуемой системы для формирования управленческих решений. Кроме того, данная методика позволяет оценить потенциал математического образования, провести его системное описание и мониторинг в контексте обеспечения качества общего математического образования, а также прогнозировать его совершенствование.

С учетом принципов целостного подхода, в рамках которого математическое образование в школах рассматривается как системноцелостный процесс, включающий такие фазы целостности, как 1) нецелое (несвязное); 2) целое (связное); 3) единое целое (оптимально связное) [5], были определены три качественных уровня математического образования в общеобразовательной организации:

• –    дискретный (т. е. минимально ограниченный);

• –    фрагментарный (т. е. среднефункциональный);

• –    целостно-связный (т. е. достаточно высокий).

Минимально ограниченный (дискретный) уровень организации математического образования в школах характеризуется разрозненностью, автономностью компонентов математического образования как образовательной системы, отсутствием согласованности ценностей, целей, технологических подходов, внешних связей, однообразием предложенных об- разовательных услуг. Кроме того, образовательный процесс обучения математике в школе носит замкнутый характер (40–59).

Среднефункциональный (фрагментарный) уровень организации математического образования в школах характеризуется тем, что целостно-объединяющее единство элементов системы «математическое образование в школе» носит локальный характер и не характеризуется систематичностью: принятие целей и ценностей математического образования носит эпизодический характер; участие в организации математического образования администрации, учителей математики носит фрагментарный характер (60–79).

Целостно-связный (высокий) уровень организации математического образования в школах характеризуется целостностью, комплексностью, организованностью, многообразием, вариативностью предложенных образовательных услуг, соответствием математического образования социально-экономическому контексту и педагогическим реалиям (80–100).

Все перечисленные уровни качества (организации) математического образования связаны между собой непрерывно: каждый из последующих уровней обязательно включает в себя все предыдущие и потенциально вносит в них качественные изменения.

Описанный диагностический инструментарий для оценки качества математического образования в общеобразовательных органи-

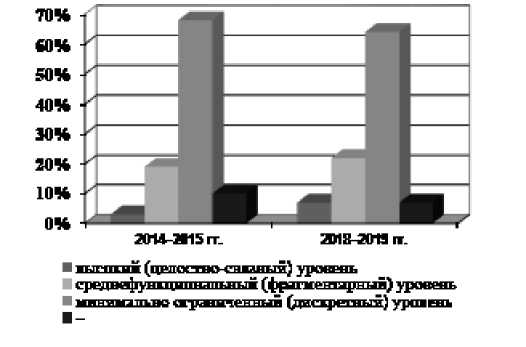
Рис. 2. Диаграмма изменения качества математического образования в общеобразовательных организациях

зациях образует развернутую характеристику конечного результата педагогической деятельности. Это необходимо для определения педагогических целей и содержания математического образования, реализуемого в образовательных организациях; для отбора педагогических концепций и технологий, обеспечивающих достижение качества математического образования с учетом социально-экономического контекста и педагогических реалий.

Представленная системно-комплексная диагностика качества математического образования апробировалась в общеобразовательных организациях различного типа (ОО, гимназии, лицеи) г. Волгограда и Волгоградской области на протяжении 5 лет (с 2014 по 2019 г.). В качестве жизненного цикла модели математического образования в общеобразовательных организациях рассматривался учебный год. Одна из задач проводимой диагностики заключалась в выявлении эффективности реализуемого математического образования в общеобразовательных организациях в количественных и качественных показателях. В течение учебного года, кроме того, имело место квалиметриче-ское сопровождение образовательного процесса обучения математике, что способствовало совершенствованию образовательного процесса, обеспечивая информацию о его состоянии на основе выбранных критериев и показателей, свидетельствующих о динамике внутренних изменений, а также о динамике изменений его субъектов. Опытно-экспериментальное исследование велось самим исследователем в сотрудничестве с учителями и руководителями образовательных организаций. Использовался системный мониторинг, который включал разные методы сбора информации, такие как внутренний и внешний аудит, педагогическое наблюдение, анкетирование, интервьюирование, индивидуальные и групповые беседы с учащимися и учителями, метод самооценки и экспертных оценок, рефлексивный анализ продуктов профессиональной деятельности учителей математики, оказывающих воздействие на качество математического образования в общеобразовательных организациях.

При проведении системно-комплексной диагностики качества математического образования в общеобразовательных организациях Волгограда и Волгоградской области учитывался тот факт, что учителя математики проходят обучение проектированию целостного учебного процесса обучения математике на инновационной основе в Волгоградской государственной академии последипломного образования [10].

Таблица 2

Динамика изменений качества математического образования в общеобразовательных организациях

Уровни организации математического образования в общеобразовательной организации

Целостно-связный (высокий)

Среднефункциональный (фрагментарный)

Минимально ограниченный (дискретный)

18    19    19    22

62   64

В результате системно-комплексной диагностики качества математического образования в общеобразовательных организациях Волгоградской области получен обобщенный показатель качества, равный Q = 0,52 (52%), что позволяет констатировать, что в Волгоградской области преобладает недостаточная подготовка выпускников общеобразовательных организаций по математике. Это обстоятельство подтверждается результатами ЕГЭ по математике (качество предметных знаний колеблется от 42 до 43%). Степень математической образованности учащихся все последние годы стабильно сохраняется на уровне элементарной грамотности.

Таблица 3

Распределение общеобразовательных организаций, участвующих в системно-комплексной диагностике качества математического образования, по уровням

Уровни качества математического образования в общеобразовательной организации

Целостно-связный (высокий)

Среднефункциональный (фрагментарный) Минимально ограниченный (дискретный)

19    18    19    19    22

67   62   64

Результаты оценки качества математического образования в общеобразовательных организациях позволяют дать качественную (развернутую) трактовку, что помогает выбирать направления коррекции и повышения качества математического образования в общеобразовательных организациях. Анализ результатов системно-комплексной диагностики качества математического образования в общеобразовательных организациях г. Волгограда и Волгоградской области позволил выделить причины и обстоятельства, являющиеся серьезными препятствиями к достижению тех целей, которые задаются ФГОС [13] и Концепцией развития математического образования [8]. Сюда относятся:

– авторитарный стиль управления качеством математического образования в общеобразовательных организациях;

– недостаточная поддержка баланса интересов всех субъектов математического образования, недостаточное использование ресурсов общеобразовательных организаций;

– закрытость учителей математики по отношению к изменениям во внешней среде и неготовность к реализации инновационных методов, средств и технологий на практике;

– преобладание репродуктивных форм организации учебной деятельности обучающихся, не способствующих раскрытию их индивидуальности и творческого потенциала.

Описанная выше методика оценки качества математического образования в общеобразовательных организациях может рассматриваться как методологическая основа для подобных оценок качества образования.