Оптимизация конструкции кристаллизатора с воздушным охлаждением

Кристаллизат в барботажном кристаллизаторе представляет собой трехфазную систему: меласса (жидкая фаза), кристаллы (твердая фаза) и охлаждающий воздух (газ). Температурные режимы охлаждения и интенсивность перемешивания кристаллизата напрямую зависят от взаимодействия жидкостной и газообразной фазы. С целью оптимизации условий протекания процесса кристаллизации далее проведен теоретический анализ гидро- и термодинамических параметров отдельного воздушного пузырька в кристаллизате.

Образование воздушных пузырьков в кристаллизаторе происходит при истечении охлаждающего воздуха из специального распределительного устройства.

Учитывая, что плотность кристал-лизата ркр=1300 кг/м3; поверхностное натяжение кристаллизата о=42,5^10-3 Н/м; кинематическая вязкость кристаллизата n = 16,16x10-6 м2/с; динамическая вязкость кристаллизата ркр = 21^10-3 Па^с; критерий Прандтля для воздуха Ргв=0,703; удельная теплоёмкость кри

сталлизата скр=3290 Дж/(кп°С); тепло-

Вт проводность кристаллизата λ=0,6     ;

м ⋅ К

Вт теплопроводность воздуха λ=0,026 м⋅К и полагая, что начальная температура кристаллизата tнкр = 60 ° С; конечная температура tккр = 10 ° С; температура охлаждающего воздуха tв = 5 ° С; средняя разность температур между воздухом и кристаллизатом △tср = 30 ° С про-ведеманализгидро-итермодинамических параметров воздушного пузырька в кри-сталлизате.

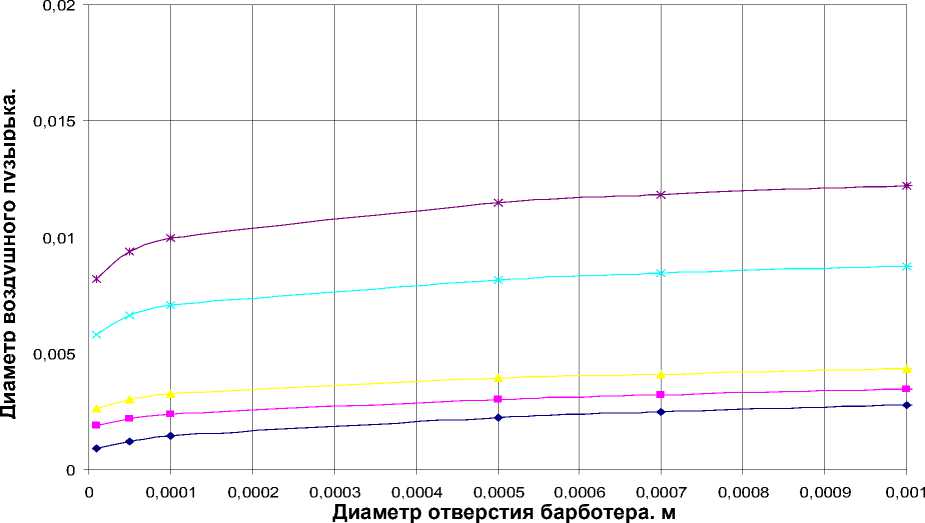
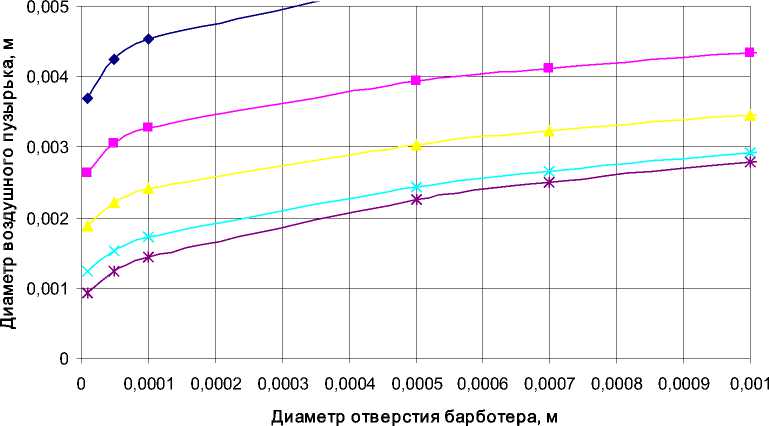
Зависимость размера воздушного пузырька от диаметра отверстия в барботере и расхода воздуха через отверстие представлена на рис. 1. Получается, чем больше расход воздуха, даже при одном и том же диаметре отверстия барботера, тем больше диаметр воздушного пузырька. Причем увеличение диаметра отверстия, например в 10 раз, от 0,0001 м до 0,001 м ведет к незначительному увеличению диаметра воздуш-

Таблица 1 – Основные термо- и гидродинамические параметры воздушного пузырька в кристаллизате

Скорость истечения воздуха, м/с	( П ,2) w = V 1 n---d 1 / I 4     )		(1)
Критерий Фруда	Fr =--- g^		(2)
Критерий Вебера	w2 d p™ Ws =---^ CT		(3)
Параметр режима истечения воздушного пузырька	( и^2 V ф = 1 + 1+---		(4)
Средние диаметры образующихся воздушных	5 = 0,9 • при Ф<27:	1 ( 3 • ^ • d ) 3 Jr • Ф 2 ( Pp • g J	(5)
пузырьков, м	5 = 0,5 при Ф>27:	1 1 3 • < r • d       , •                         • 3	(6)
		I Pp • g )
Скорость подъёма пузырька, м/с	R i = 1,5• ( g • Pp • а 3 / Др 4) 0,214 ю = 0,7 • 5 1'8 /v °’5 кр		(7) (8)
	при Re1≤Re≤ Re2 Re 2 — (Рф ■ g? ca= \,91^crf(p	°'25 V-75]/^ 4'5)	(9)
	при Re≥Re2 to = 0,714 • 7 g • 5		(10)

Продолжение Таблицы 1

V 1 = 0,110 - 6 м³/с.

Рассмотрим термодинамические ха

рактеристики воздушного пузырька, выходящего из отверстия d=0,0007 м.

Представляет интерес интенсив ность изменения теплопередачи между

V1 V2

V3 V4 V5

Рис. 1. Зависимость диаметра воздушного пузырька от диаметра отверстия в барботере и расхода воздуха через отверстие: V 1 = ^0,1 ‘ 10 м³/с; V 2 = ^0,5 ‘ ¹⁰ - 6 м 3 /с; V₃= ^0,1 ‘ ¹⁰ - 5 м 3 /с; V 4 = ^0,5 ‘ ¹⁰ - 5 м 3 /с; V 5 = ^0,1 ‘ ¹⁰ - 4 м 3 /с

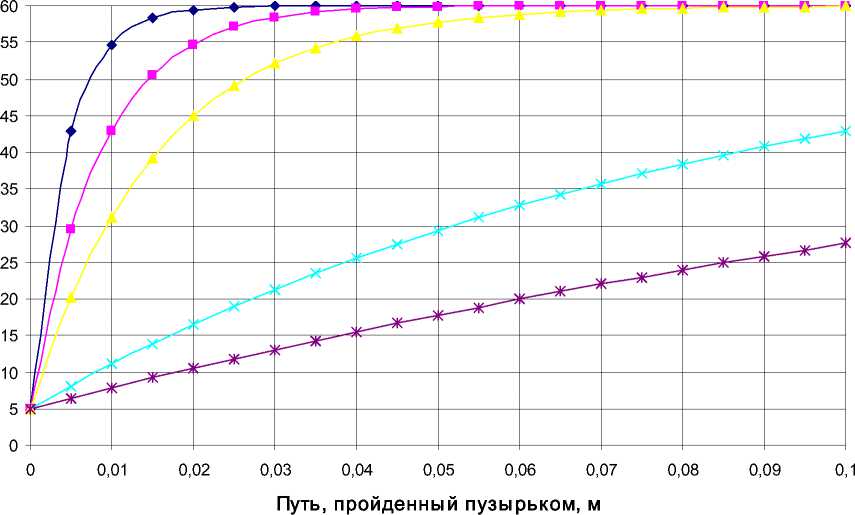
воздушным пузырьком и кристаллиза-том в процессе его движения. Если принять весь путь, пройденный всплывающим пузырьком h=0,1 м и разделить его на участки по 0,5 мм, принимая на каждом участке температуру пузырька постоянной и равной его температуре на выходе из предыдущего участка, то изменение температуры по участкам будет соответствовать кривым на рис. 2.

Из рисунка 2 видно, что чем меньше подача воздуха и, соответственно, меньше размер воздушного пузырька, тем быстрее он нагревается до максимально возможной температуры, которая приближается к температуре кристаллиза-та. Если при маленьких расходах V1= 0,1 ‘ 10 ^{- 6} м³/с, V 2 = 0,5 ‘ 10 ^{- 6} м³/с и V₃= 0,1 ‘ 10 ^{- 5} м³/с пузырек на пути h=0,1 м успевает нагреться до температуры кристалли-зата, то при повышении расхода до V₄=

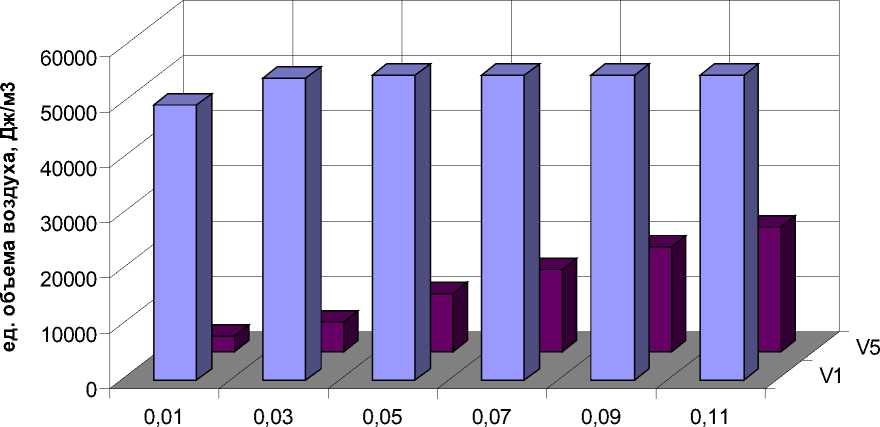
0,5 ‘ 10 ^{- 5} м³/с и выше - он нагревается всего до 43 ° С. Чем больше расход, тем меньше используется теплоотводящая способность воздуха. Это подтверждает зависимость, представленная на рис. 3.

Поскольку цель воздушного охлаждения – отбор тепла от кристаллизата, который осуществляется в конкретном аппарате, то представляет интерес анализ влияния конструктивных и эксплуатационных параметров кристаллизатора. Основным элементом кристаллизатора, определяющим процесс теплопередачи между воздухом и кристаллизатом, является барботирующее устройство, в частности диаметр отверстий для выхода воздуха d и их количество n.

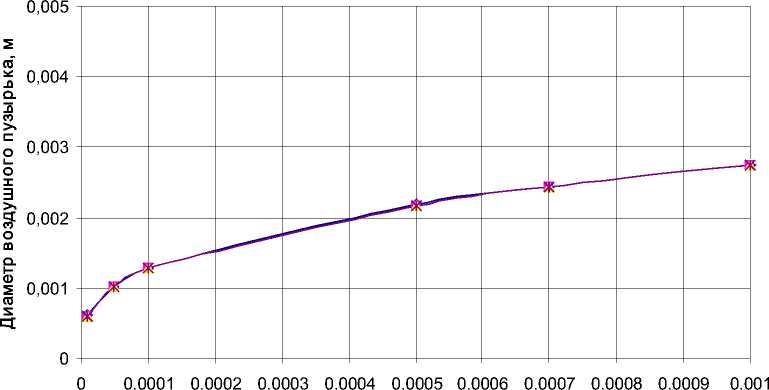
Проведем анализ влияния диаметра отверстий барботера и их количества на диаметр образующихся воздушных пузырьков при небольшом расходе воздуха V= ^0,1 ‘ ¹⁰ м³/с (рис. 4).

V1 V2 V3 V4 V5

Рис. 2. Изменение температуры воздушного пузырька, выходящего из отверстия диаметром d = 0,0007 м с начальной температурой t_н = 5 ° С в кристаллизат с температурой t_кр = 60 ° С на пути h = 0,1 м при расходах воздуха V 1 = ^0,1 1 ⁰ м³/с; V 2 = 0,5 • 10 - 6 м³/с; V₃= 0,1 • 10 - ⁵ м³/с; V 4 = 0,5 • 10 - ⁵ м³/с; V₅= ^0,1 • ¹⁰ м³/с

Как видно из рис. 4. количество отверстий при малых расходах воздуха практически не влияет на размер образующихся воздушных пузырьков. При увеличении расхода это влияние становиться заметным (рис. 5).

При малых расходах воздуха частота образования пузырьков из одного отверстия при малом их количестве, например n = 5, во много раз больше частоты образования пузырьков из барботера с большим количеством отверстий. Таким образом, общее количество пузырьков, находящееся в кристаллизате и их диаметр, не зависят от количества отверстий в барботере.

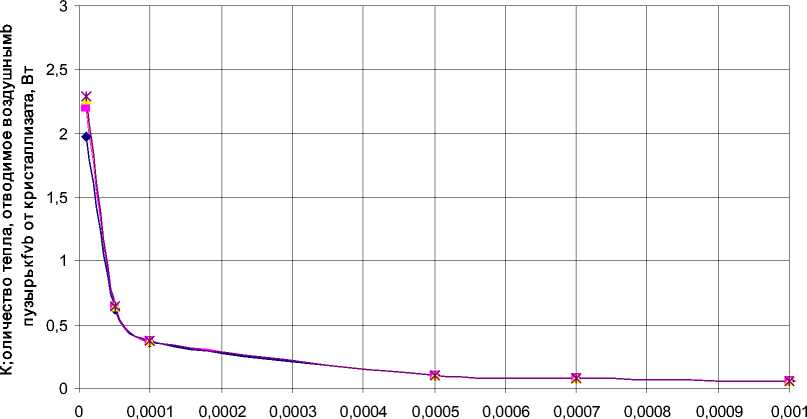
Аналогичным образом количество тепла, отводимое всеми воздушными пузырьками, образующимися при барботировании, при постоянном малом расходе практически не зависит от количества отверстий в барботере, причем интенсивность теплоотвода повышается при уменьшении диаметра его отверстий (рис. 2.12).

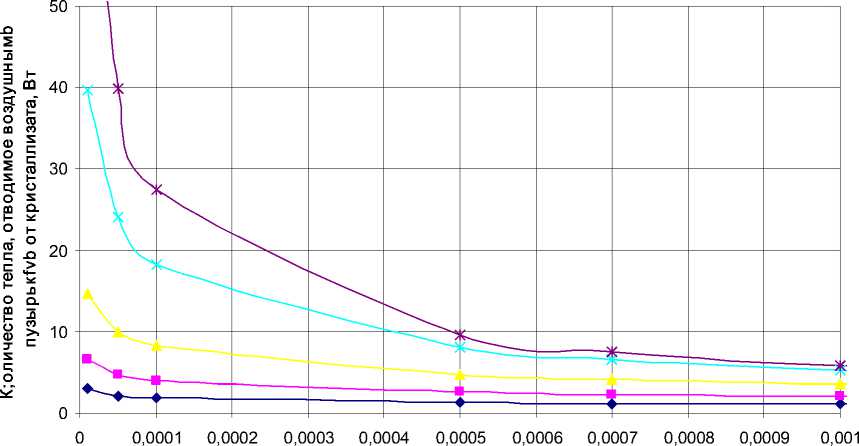
При увеличении расхода воздуха количество тепла, отводимое пузырьками, начинает существенно зависеть от количества отверстий в барботере (рис. 7).Анализ показал, что чем меньше диаметр отверстий барботера, тем эффективнее теплоотвод от кристаллизата к воздушным пузырькам. Это объясняется тем, что поверхность теплопередачи увеличивается при неизменном расходе воздуха и уменьшении диаметра воздушных пузырьков. Однако при неизменном количестве отверстий в барботере и расходе воздуха уменьшение площади сечения отверстий выхода

т

V1 V5

Рис. 3. Количество тепла, забираемого воздухом (на 1 м³) в процессе движения его в кристаллизате, при минимальном и максимальном расходах V 1 = ^0,110 - 6 м 3 /с и V 5 = 0,1 - 10 - 4 м 3 /с

Диаметр отверстия барботера, м n=5      n=10      n=20      n=50      n=100

Рис. 4. Зависимость диаметра образующегося воздушного пузырька от диаметра отверстий барботера при расходе воздуха

V= 0,1 ⋅ 10

-

6 м³/с.

n=5      n=10      n=20      n=50      n=100

Рис. 5. Зависимость диаметра образующегося воздушного пузырька от диаметра отверстий барботера при расходе воздуха V= ^0,1 " ¹⁰ м³/с

Диаметр отверстия в барботере, м

n=5

n=10

n=20

n=50

n=100

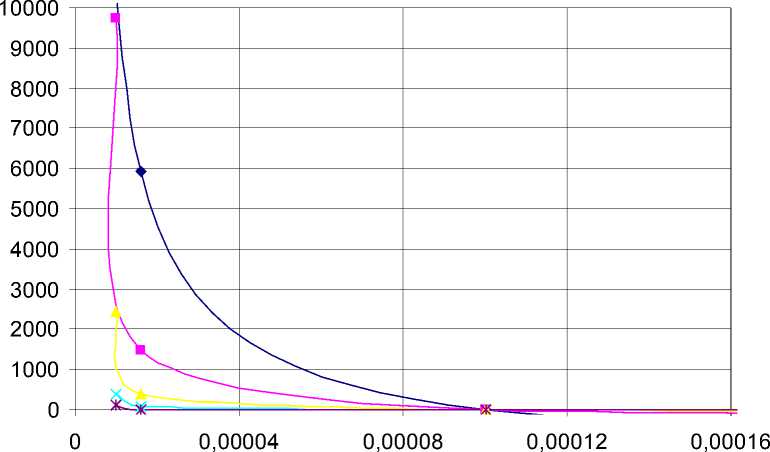
Рис. 6. Зависимость влияния конструктивных параметров барботирующего устройства на теплопередачу между воздушными пузырьками и кри-сталлизатом при расходе воздуха V= 0,110 м3/с воздуха потребует увеличение давления подачи воздуха в кристаллизатор. Проведем оценку зависимости давления воздуха от диаметра отверстий и их количества (рис. 8).

С учетом формулы (1):

_P = 16 ⋅ ρ в ⋅ V ² 2 ⋅ n ² ⋅ π ² ⋅ d ⁴ ,

Диаметр отверстия в барботере, м

n=5

n=10

n=20

n=50

n=100

Рис. 7. Зависимость влияния конструктивных параметров барботирующего устройства на теплопередачу между воздушными пузырьками и кристаллизатом при расходе воздуха V= 0,1 - 10 - 4 м³/с

т т т          т

n=5 n=10 n=20 n=50 n=100

Рис. 8. Зависимость давления подачи воздуха от диаметра отверстий барботера при расходе воздуха V= 0,110 м3/с где рв - плотность воздуха при ат- мосферном давлении и t = 5 ° С, Рв в.

1,3 кг/м3.

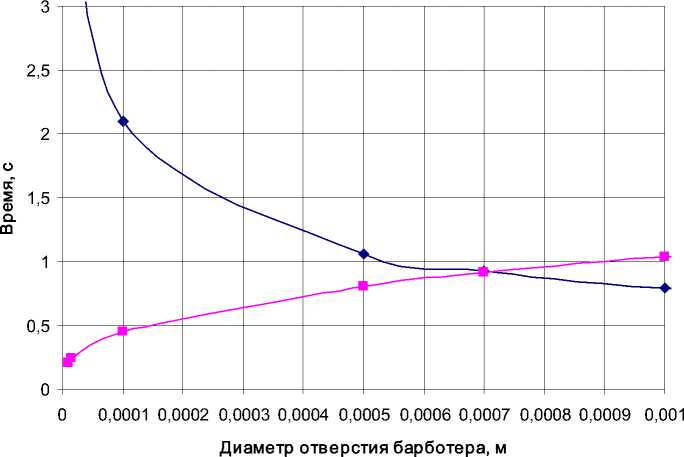
Время подъема воздушного пузырька, с

Время нагрева воздушного пузырька, с

Рис. 9. Определение оптимального диаметра отверстия барботера для кристаллизатора высотой h=0,1 м при расходе воздуха V= ^{0,1 ⋅ 10 - 6} м3/с независимо от количества отверстий

Как и следовало ожидать, с уменьшением диаметра отверстий барботера и уменьшением их количества давление подачи воздуха должно неограниченно возрастать, следовательно, возрастет расход энергии на подачу воздуха. Очевидным решением этой задачи является увеличение числа отверстий барботера, тем более что теплопередача при увеличении количества отверстий также интенсифицируется (рис. 7).

Следует учесть, что эффективность теплопередачи к мелким пузырькам приводит к быстрому их нагреванию, тогда при большой высоте кристаллизатора большая часть времени пребывания пузырька в нем становится бесполезной. Здесь возникает задача соотношения конструктивных параметров кристаллизатора и барботера.

Рассмотрим предельный случай. Допустим, высота кристаллизатора составляет h = 0,1 м. Определим время нагрева воздушного пузырька от начальной температуры t_нв = 5 ° С до температуры кристаллизата, которая для воздуха является предельной конечной t_кв = 60 ° С.

Сравним это время со временем подъема пузырька на предельную высоту h = 0,1 ис. 9).

Как видно из графика, существует оптимальный диаметр отверстия барботера, который составляет d = 0,0007 м и обеспечивает образование пузырьков такого диаметра, при котором время нагрева с 5 до 60 ° С равно времени подъема их в кристаллизаторе на заданную предельную высоту h = 0,1 м. Совпадающее время нагрева и подъема пузырька составит τ = 0,9 с при расходе воздуха

V= 0,110 ^{- 6} м³/с. Размер пузырька, рассчитанный по формуле (5) составил δ= 2 ⋅ 10 ^{- 3} м; скорость его подъема ^{ω = 0,11} м/с; коэффициент теплопередачи от кристаллизата к пузырьку k = 11,7 Вт/ (м²^К); количество тепла, отводимое пузырьками Q = 0.08 Вт. Все данные получены по методике (табл. 1).

Для малых расходов воздуха оптимальный размер отверстия барботера не

зависит от расхода воздуха и количества отверстий барботера и составляет d = 0,0007 м.

Рассчитаем диаметр кристаллизатора по известным высоте и ее объему, например, v=0,7 л:

D =

4 ⋅

v π ⋅ h

4 ⋅

0,7 ⋅ 10 ^{- 3}

3,14 ⋅ 0,1

≈ 0,09 м .

Таким образом, для кристаллизатора вместимостью 0,5 л выбраны оптимальные геометрические параметры: h=0,1 м; D=0,09 м; d=0,7 мм; n=5 при расходе воздуха через одно отверстие

V= ^0, 11 ⁰ — 6 м 3 /с.

Итак, в результате теоретического анализа гидро- и термодинамических параметров воздушного пузырька в кри-сталлизате установлены оптимальные соотношения между диаметром отверстия барботера и высотой кристаллизатора, обеспечивающие наиболее интенсивную теплопередачу от кристаллизата к охлаждающему воздуху в зависимости от его расхода.

FGBOU VPO the Vereschagin Vologda State Dairy Farming Academy

Air-Cooled Crystallizer Construction Optimization