Расчет теплозащитных параметров пакетов одежды методом имитационного моделирования (методом Монте-Карло)

МРНТИ 64.33.14                           

Теплозащитные свойства материалов, применяемые для одежды спортсменов экстремального вида спорта, являются наиболее сложными, зависящими от множества физических свойств материалов, составляющих пакет одежды. Среди свойств, которые определяют теплозащитные свойства одежды наиболее важным является тепловое сопротивление пакета материалов.Тепловое сопротивление пакета материалов одежды зависит от целого ряда факторов, таких как: температура, скорость движения и относительная влажность воздуха окружающей среды; воздухопроницаемость, влажность, теплопроводность пакета одежды; толщина пакета одежды, а также статическое или динамическое состояние человека [1-3].

Физико-механические параметры материалов, входящих в состав пакетов в партии, представляются рассеянными в пределах заданных допусков, т.е. являются случайными величинами и поэтому при расчетах теплофизических характеристик пакетов применение статистических методов является актуальной.

Цель исследования. Разработка метода расчета теплофизических параметров пакета одежды имитационным методом.

Материалы и методы исследований

Для расчетов суммарного теплового сопротивления материалов в условиях ветра коэффициент теплопроводности воздуха α в определяется с учетов скорости ветра по формулам [4]:

α в =2,4·v+2,33 при v ≤4 м/с, α в =3,7·v+1,163 при v ≥4 м/с.

При расчете анализа влияния ветра на тепловые показатели, можно принять скорость ветра с учетом погодных условий [5] в предгорных и горных зонах Алматинской области РК в следующих пределах v= 0, …, 15м/с.

Если считать, что рассматриваемый пакет одежды создает разность температур ( t 1 -t 2 ), слои которого имеют сопротивление R сум , тогда формула переноса тепла внутри одежды примет вид:

Ч =

tl~t2

Ять+£

m Sr, l '

¹ ^r а в

Величина эквивалентного коэффициента теплопроводности λ, такого условно однородного материала, который создает те же условия для прохождения тепла, т.е. ту же разность температур (t1 – t2) при том же тепловом потоке q, определяется формулой

Л =

8 n⁸b   m⁸r  ¹ ,

^U_b^{+L 1} ^r + а в

где δ - толщина эквивалентного (воображаемого однородного слоя), который равен 8 = L i 8_b + L ™ 8_r , тогда величина эквива-

Л =

Анализ современных данных по теплозащитным свойствам отдельных материалов одежды показал, что они довольно хорошо изучены при различных температурах и влаж-ностях внешней среды. Однако теплозащитные свойства одежды в основном изучены с учетом влияния детерминированных факторов, хотя по природе определения факторы, оказывающие влияния на теплозащитные свойства одежды имеют случайный характер. В этой связи для получения объективных значений показателей теплозащитных свойств одежды при расчетах необходимо учитывать характер распределения факторов для партии изделий, которых эффективно можно реализовать имитационным методом моделирования.

лентного коэффициента теплопроводности λ будет имет вид:

1 П 8 ь +Ү т 8 г v n⁸b,^m⁸r  ¹ *

L +L ⁺

^1ЛЬ ^{1 Л}г ^а в

Известно, что метод имитационного моделирования (метод Монте-Карло) позволяет, опираясь на строгие законы теории вероятности, свести широкий класс сложных задач к относительно простым арифметико-логическим преобразованиям выборок [6].

Для применения метода имитационного моделирования к расчету параметров теплопроводности пакета верхней одежды необходимо предварительно подготовить теплофизические данные материалов отдельных слоев пакета [7-10]. Для примера рассмотрим схему пакета одежды (рис.1).

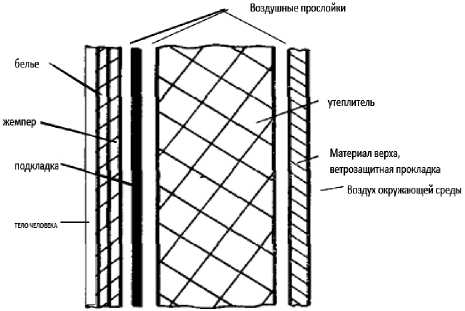
Рисунок 1. Схемаструктуры слоев пакета верхней одежды

Для определения статистических характеристик теплофизических параметров были изготовлены образцы пакетов (согласно структурной схеме рис.1) в количестве 10 шт.) и произведены замеры их параметров. Замеры параметров производились стандартными методами: толщины материалов измерялись толщиномером МТ 026, теплопроводности слоев пакета прибором SA608F [11-14].

Результаты измерений из-за погрешностей измерений, из-за различий величин деформаций материалов оказались рассеянными в определенных пределах [15-17]. По результатам замеров были определены их среднее и среднеквадратические значения, как случайных чисел, распределенных по нормальному закону. В таблице 1 приведены среднее арифметическое и среднее квадратическое отклонения (в пределах распределения ±3σ) параметров.

Таблица 1. Статистические показатели свойств слоев пакета

Номера слоя	Состав пакета	Толщина слоя, мм	Коэф. теплопроводности слоя, Вт/(м·°С)
1	белье (хлопчатобумажная майка)	<5 1 =0,4±0,3;	Л 1 =0,038±0,012
2	воздух	62 =0,05±0,05;	Л2 = 0,020±0,008
3	жемпер	<5 3 = 0,8±0,4;	Л 3 =0,042±0,014
4	воздух	<5 4 = 0,05±0,05;	Л 4 =0,020±0,008
5	подкладка	<5S = 0,15±0,2;	Л5 =0,040±0,014
6	воздух	<56 = 0,05±0,05;	Л6 =0,020±0,008
7	утеплитель	<57 = 1,5±1,0;	Л7 =0,038±0,012
8	воздух	<5 8 = 0,05±0,05;	Л 8 = 0,020 ±0,008
9	ветрозащитная подкладка	<59 = 0,27±0,1	Л9 =0,042±0,014
10	воздух	<510 = 0,05±0,05	Л10 =0,038±0,012

Для расчета суммарного теплового сопротивления и эквивалентной теплопроводности имитационным методом (методом статистических испытаний) необходимо рассмотреть партию пакетов в количестве N.

Рассмотрим алгоритм расчета параметров теплопроводности методом статистических испытаний (методом Монте-Карло).

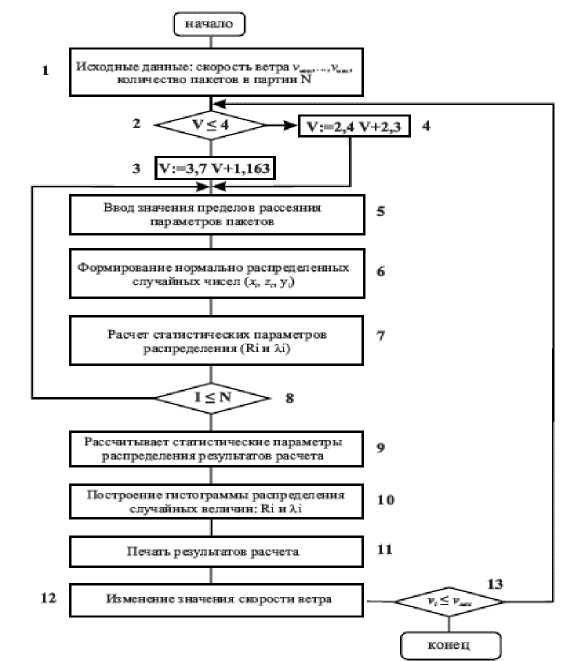
Блок схема расчета теплозащитных свойств пакта материалов одежды приведена на рисунке 2.

Как следует из рисунка 2, основными блоками алгоритма моделирования являются:

блок 1 - ввод начальных данных, включающий задание предела изменения значений скорости потока воздуха и мин ,-, У маі , количество пакетов в рассматриваемой партии пакета;

блоки 2, 3, 4 - определяют зависимости скорости ветра, по какой формуле определить коэффициент теплопроводности воздуха v := а в ;

блок 5 - ввод пределов рассеяния теплофизических параметров слоев пакета х i, min ≤х i ≥x i, max ; z i, min ≤z i ≥z i, max ;у i, min ≤у i ≥у i, max ;

блок 6 - генерирует нормально распределенные случайные числа для каждой переменной ( x i , z i , у i) в соответствии с заданными параметрами распределения и вычисляет значение уравнения.

блок 7 - производит вычисления статистических параметров распределения результатов (суммарного теплового сопротивления R и эквивалентного коэффициента теплопроводности Л пакета), такие как: среднее значение, стандартное отклонение, дисперсию, минимальное и максимальное значения.

блок 8 - проверяет условия: выполнен ли расчет для всех пакетов в партии, по i > N;

блок 9 - рассчитывает статистические параметры распределения результатов расчета:

п— ^і Ri         /1 [vN г>2   1 fV^ D АІ/с\

R=,°R = Jn-П^ r^ - N(s R‘)J

Л=^,       = Jj-jisM-ja:?^

р ас пре “с ле ни я р езул ьтятов рас че та

Построение гистограммы распределения

Печать результатов расчета

Изменение значения старости ветра

Ввод значения пределов рассеяния параметров пакетов

Формирование нормально рас пред еденных случайных чисел (х^ z„ yj

Расчет статистических параметров распределения ( Ri и Xi)

Исходные данные: скорость ветра v_ таличество пакетов в партии N конец

Рисунок 2. Блок-схема расчета теплозащитных параметров пакетов

блок 10 - строит гистограммы распределения результатов R и Л, используя библиотеку matplotlibpython .

блок 11 - производит вывод статистических параметров распределения на печать;

блок 12 - меняет значение скорости воздуха v и расчет повторяется до тех пор, пока все значения скорости не будут учтены.

Блок 13 – организация цикла расчета по скорости ветра.

На основе этого алгоритма составлена программа на языке программирования Python. Для удобства составления программы произведены некоторые параметры переименования в расчетных уравнениях. Программа расчета составлена при значениях коэффициента теплопроводности воздуха а, определяемого с учетом скорости ветра по формулам:

а =2,4· v +2,33 при v ≤4 м/с,

а =3,7· v +1,163 при v ≥4 м/с.                                    (4)

После замены обозначений в уравнениях (1), (2), (3) и (4) они преобразуется в следующие виды:

хb=х1+х2+х3+х4+х5

уm=у1+у2+у3+у4+у5 hс=хb+уm

Rb=х1/z1+x2/z3+x3/z5+x4/7+x5/z9

Rm=y1/z2+y2/z4+y3/z6+y4/z8+y5/z10

R=Rb+Rm+1/ a

Lc=hc/R.                                                (4)

При этом аргументы уравнения принимают значения нормально распределенных чисел в пределах:

0,1≤х1≥0,7

0,026≤z1≥0,05 0,1≤у1≥0,10 0,012≤z2≤0,028 0,4≤х2≥1,2 0,028≤z3≥0,056 0≤у2≤0,10 0,012≤z4≥0,028 0,13≤х3≥0,17 0,026≤z5≥0,054 0≤у3≥0,10 0,012≤z6≥0,028 0,5≤х4≥2,5 0,026≤z7≥0,05

0≤у4≥0,1

0,012≤z8≥0,028 0,17≤х5≤0,37 0,028≤z9≥0,056 0,1≤у5≥0,2 0,026≤z10≥0,05

При выборе скоростей ветрового потока исходим из условной шкалы Бофорта для визуальной оценки силы (скорости) ветра в баллах и рекомендации МЧС Казахстана [18], что согласно шкале Бофорта, оценивается по двенадцатибальной шкале (табл. 2).

Таблица 2. Шкала Бофорта

Баллы Бофорта	Средняя скорость ветра	Определение силы ветра
0 баллов	0,0 - 0,2 м/с	Штиль
1 баллов	0,3 - 1,5 м/с	Тихий ветер
2 баллов	1,6 - 3,3 м/с	Легкий ветер
3 баллов	3,4 - 5,4 м/с	Слабый ветер
4 баллов	5,5 - 7,9 м/с	Умеренный
5 баллов	8,0 - 10,7 м/с	Свежий ветер
6 баллов	10,8 - 13,8 м/с	Сильный ветер
7 баллов	13,9 - 17,1 м/с	Крепкий ветер
8 баллов	17,2 - 20,7 м/с	Очень крепкий
9 баллов	20,8 - 24,4 м/с	Шторм
10 баллов	24,5 - 28,4 м/с	Сильный шторм
11 баллов	28,5 - 32,6 м/с	Жестокий шторм
12 баллов	32,7 и более	Ураган

МЧС Казахстана предоставило данные по обеспечению безопасности туристов в горной местности и рекомендации по проведению туристических походов при силе ветра до 7 баллов по шкале Бофорта, и сучетом этого скорость ветра считается меняющейся в пределах: 1,10 м/с.

Расчеты произведены для пакетов в (N) количестве партии (условно принимаем N=300).

Результаты и их обсуждение

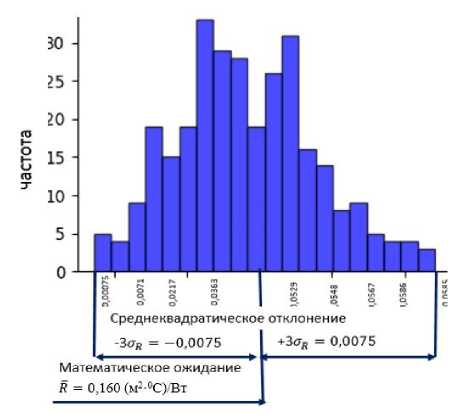
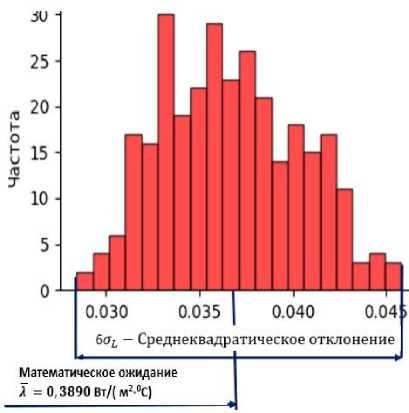
В результате определены статистические параметры распределения суммарного эквивалентного сопротивления R и эквивалентного коэффициента теплопроводности L, для них построены гистограммы распределения (рис. 3) [9-12].

• а)    Гистограмма распределения суммарного, эквивалентного сопретивление пакета R.

• б)    Диаграмма распределения эквивалентного коэффициента теплопроводности пакета λо.

Рисунок 3. Гистограммы распределения тепловых параметров пакета одежды, полученные методом статистического моделирования (методом Монте-Карло)

Статистические параметры результатов расчета рассматриваемого пакета приведены в таблице 3 .

Таблица 3. Результаты расчета суммарного теплового сопротивления и эквивалентного коэффициента теплопроводности

Скорость воздуха V, м/с	Средее значение суммарного сопротивления пакета, R, (м2·0С)/Вт	Среднеквадратическо е отклонение суммарного сопротивления ± 3 σ R	Среднее значение эффективного коэффициента теплопроводности, Л, Вт/( м2·0С)	Среднеквадратическо е отклонение коэффициента теплопроводности ± 3 σ λ
0	0,240	0,050	0.2392	0,01500
2	0,220	0,040	0.2623	0,01620
4	0,200	0,030	0.2863	0,01600
6	0,180	0,040	0,3012	0,01700
8	0,160	0,030	0,3596	0,01756
10	0,140	0,020	0,3792	0,02001
12	0,120	0,120	0,3980	0,02150
14	0,010	0,060	0,4089	0,02025

На рисунке 4 приведен график распределения суммарного теплового сопротивления, а на рисунке 5 – график изменения эффектив- ного коэффициента теплопроводности пакетов в зависимости от потока ветра окружающей среды.

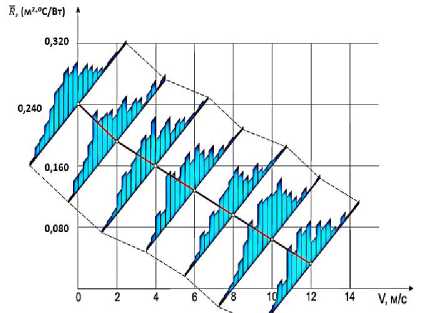
Рисунок 4. График распределения суммарного теплового сопротивления в зависимости от скорости воздуха

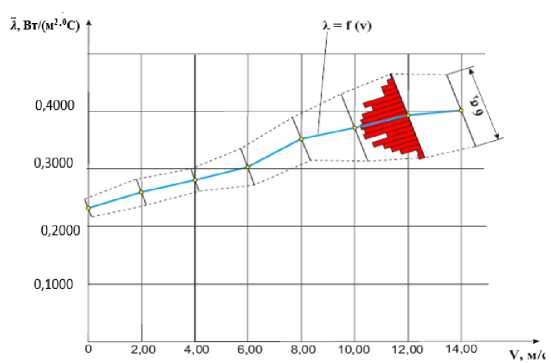
Рисунок 5. График изменения эффективного коэффициента теплопроводности пакетов в зависимости от потока ветра окружающей среды.

Заключение, выводы

Применение метода имитационного моделирования к расчету теплопроводности пакета верхней одежды для спортсменов горного туризма позволил получить результаты, близкие к реальным.

Разработанная программа расчета теплофизических характеристик пакета материалов одежды позволяет в процессе вычислений изменять параметры модели: вводить новые слои материалов в пакет, изменять теплофизические и линейные характеристики отдельных слоев пакета, изменять внешние условия.

Как показали результаты расчетов с увеличением скорости потока ветра значения эффективного коэффициента теплопроводности пакетов увеличиваются, тогда как значения суммарного коэффициента пакетов в партии снижаются, что связано с уменьшением воздушных пространств вследствии деформации пакетов.

Данную программу расчета теплофизических характеристик пакета материалов одежды можно использовать в процессе проектирования утепленной верхней одежды, изменяя параметры модели: вводить новые слои материалов в пакет, изменять теплофизические и линейные характеристики отдельных слоев пакета, изменять внешние условия.