Уточненный тепловой расчет кристаллизатора для двухступенчатого охлаждения сгущенных молочных консервов с сахаром

В технологических процессах производства продуктов питания особое место, в силу своеобразия условий теплопередачи, занимает охлаждение таких высоковязких пищевых жидкостей, как сгущённое молоко с сахаром, высокожирные сливки, сметана, смеси для приготовления мороженого и маргарина, животные жиры, овощные и фруктовые пюре, кондитерские и косметические кремы, пищевые клеи и др.

Теоретические исследования [1] и практический опыт показали, что охлаждение таких продуктов, особенно меняющих при этом своё агрегатное состояние, наиболее эффективно осуществляется в пластинчатых скребковых теплообменных аппаратах (рисунок 1), который представляет собой набор чередующихся теплообменных и, так называемых, продуктовых пластин, установленных и зажатых на специальных штангах. При этом внутри продук- товых пластин расположены подвижные диски, закреплённые на валу. С обеих сторон этих дисков подвижно закреплены полиамидные ножи. При вращении дисков эти ножи счищают с поверхности теплообменных пластин пристенный ламинарный слой обрабатываемого продукта, при этом происходит его перемешивание.

Целью настоящих исследований явилось уточнение методики теплового расчета скребкового теплообменного аппарата.

Как известно, тепловой расчёт сводится к определению теплопередающей поверхности:

Q ( "1+z f+~ f =  ^ g Л a 2 J

^ t ср , где a1 - коэффициент теплоотдачи, от продукта к стенке, Вт/м2·К;

a ₂ - коэффициент теплоотдачи от

Рисунок 1. Скребковый пластинчатый теплообменный аппарат

стенки к хладоносителю, Вт/м2·К;

Σ ^δ

λ – термическое сопротивление материала стенки, Вт/К.

Для расчёта теплопередающей поверхности необходимо знать величину коэффициента теплоотдачи, который

m - вязкость теплопередающей среды, Па·с;

Re _J - критерий Рейнольдса, учитывающий режим поступательного движе- _{Re ϑ =} ϑ ⋅ d э ⋅ ρ

ния продукта в аппарате,

µ

;

определяется следующим образом:

• - при переносе тепла от продукта стенке:

• α ₁ = A у/λ ⋅ C ⋅ ρ ⋅ n , ( 1 )

к

-

при переносе тепла от стенки

к

хладоносителю:

α = Nu⋅λ=A⋅Re m ⋅Pr n⋅Re k 2        мж ϑ dэкв                              , ( 2 )

_{Re =} n ⋅ D ² ⋅ ρ м

где

^µ – критерий Рей-

нольдса для условий перемешивания;

n – частота вращения рабочего органа, с-1;

D – диаметр рабочего органа, м;

r

–

среды,кг/м3;

плотность теплопередающей

J – скорость поступательного движения, м/с;

dэ – эквивалентный диаметр канала, образованного диском рабочего органа, теплообменной стенкой и скребками;

Pr_ж - критерий Прандтля, ^{ж а ⋅ ρ} ;

а – коэффициент температуропроводности среды, м2/с.

Раскрывая значения критериев, и введя под корень число скребков z, находим:

α ₁ = Aу/ λ ⋅ C ⋅ ρ ⋅ n ⋅ z , ( 3 )

где А – коэффициент перед радикалом, найденный аналитически.

Ранее отмечалось, что величина коэффициента А зависит от конструктивных особенностей рабочих органов

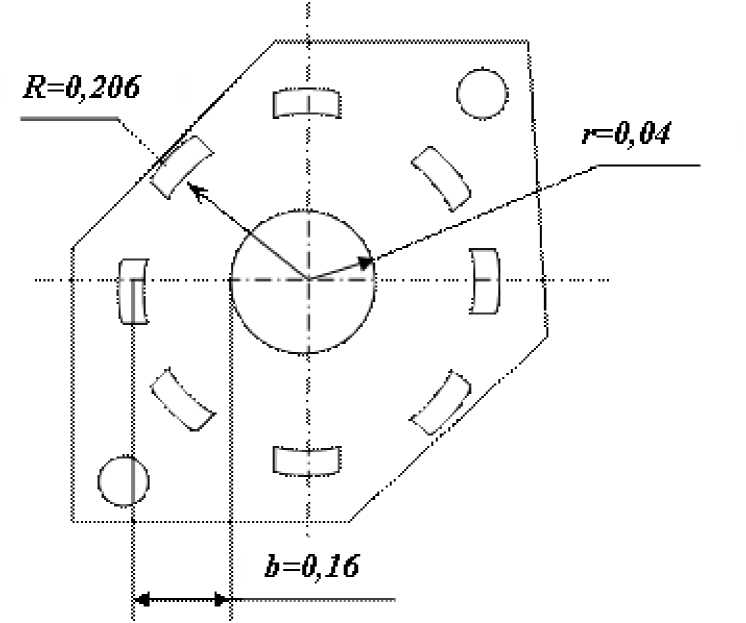
Рисунок 2. Схема пластины

(рисунок 2), точности изготовления и теплофизических свойств жидкости.

Величина коэффициента А определялась следующим образом. Из литературы известно [2], что:

Nu = 0,023 Re 0,8 Pr⁰ , ⁴ , ( 4 )

откуда следует:

а г = 0,023 — Re^0,8 Pr^{0,4 dэкв}             , ( 5 )

где a2 – коэффициент теплоотдачи от стенки к охлаждающей жидкости, Вт/ м2К ;

l _рас - средний коэффициент теплопроводности, Вт/м²К;

dэкв – эквивалентный диаметр, м, определяемый как:

d = f экв П где f - площадь поперечного сечения канала в теплообменной пластине, м2;

П – часть контура, участвующего в теплообмене, м.

В нашем случае dэкв = 2h, где h – высота канала, м.

Re - критерий Рейнольдса, определялся как р   512 h

Re = v где J - скорость движения рассола в канале теплообменной пластины, определялась как:

^_ Gpacmeop f Р ;

^Срас.теор. ^- расход рассола, КГ/С;

n - среднее значение коэффициента кинематической вязкости, м²/с;

Известно, что коэффициент теплопередачи равен:

К =1   8 Г

« 1 \ т ^а 2 , ( 6 )

где d – толщина теплопередающей стенки, м;

Х ет - коэффициент теплопроводности стенки, Вт/м² К

1 α ^{1 =} 1 δ 1 —

Откуда, ^{К λ ст α 2} ( 7 )

Подставляя найденное значение α1 в формулу (1), получим выражение для расчёта коэффициента А для нашего охладителя:

методике для сгущённого молока с сахаром коэффициент перед радикалом составит А = 0,65.

Таким образом, уточнённая нами формула для расчёта α1 будет иметь вид:

α ₁ = 0,65 λ ⋅ c ⋅ ρ ⋅ n ⋅ z ( 9 ).

A =       α ¹

V λ _см ⋅ С_см ⋅ ρ ⋅ n ⋅ z ( 8 )

Обработка экспериментальных данных показала, что для теплообменников, изготовленных на основе вновь разработанной пластины по приведённой выше