Прикладные задачи в обучении математике учащихся 12–15 лет в России и Германии

Одной из основных задач современного школьного образования является усиление прикладной направленности школьного курса математики с целью повышения качества математического образования, а также для развития у учащихся умения применять полученные знания при решении задач в реальной жизни. Многие отечественные ученые-методисты занимались исследованием прикладной направленности обучения математике (Н.А. Терешин [11], И.М. Смирнова и В.А. Смирнов [10], М.В. Егупова [1] и др.). В работах С.Н. Дворяткиной, Е.Н. Эрентраут, Н.Я. Виленкина, Г.В. Дорофеева, Ю.М. Ко-лягина рассматриваются идеи реализации прикладной направленности школьного курса математики. Основным средством ее реализации является решение прикладных задач. Н.А. Терешин дает такое определение: «прикладная задача – это задача, поставленная вне математики и решаемая математическими средствами» [11, с. 6]. К ним будут относиться задачи с определенным сюжетом, описывающим некоторую проблему и имеющим практическое значение, при этом процессы и объекты задачи должны быть реальными.

В Германии в начале XXI века после реформирования школьного математического образования его содержание кардинально изменилось, прежде всего за счет усиления прикладной направленности обучения. За более чем 20-летнюю историю проведения мониторингового исследования PISA лишь нескольким странам удалось внести изменения в образовательный процесс и существенно улучшить образовательные результаты учащихся. Германия была одной из таких стран, в 2015 году по результатам исследования PISA она вошла в группу стран с высокими результатами образовательных достижений в Европе [7]. Несмотря на снижение образовательных результатов немецких школьников в исследовании PISA-2022 года, опыт Германии в реализации прикладной направленности школьного курса математики представляет интерес.

Следует сказать, что геометрия как отдельный курс в школах Германии не изучается. Курс математики 5–10 классов и экзамены BBR-9 и MSA-10 (аналог ГИА-9 в России) содержат немалое количество прикладных задач, в частности, функциональной линии, линий геометрических фигур и преобразований. Изучение немецких экзаменационных материалов и учебной математической литературы [13; 18–20] позволяет сформировать представление об опыте Германии в обучении математике учащихся 12–15 лет. Данный опыт полезно изучить, выделив удачные практики, которые можно использовать в российском математическом образовании.

Таблица

Особенности содержания обучения математике в России и Германии

Россия	Германия
1. Уделяется внимание взаимосвязи изучаемых элементов содержания, теоретический блок информации достаточно большой, особенно в классах с углубленным изучением математики.	1. Уделяется внимание взаимосвязи изучаемых элементов содержания и проблемных ситуаций из жизни. Блок информации ограничен, но достаточен для решения большого количества прикладных заданий.
2. С обычным калькулятором как инструментом для вычислений ученики знакомятся в конце 5-го класса. Далее в учебниках его использование предусмотрено в единичных заданиях. В ФРП по математике [12] для 8–9-х классов сформулировано требование «использовать при необходимости калькулятор» для отдельных вопросов содержания (находить квадратные корни, вычислять значение дроби, значения функций, заданных формулами и т.п.). Компьютер и цифровые ресурсы предлагается использовать при изучении курса «Вероятность и статистика». Научные калькуляторы в обучении математике не используются.	2. Научные калькуляторы являются обязательным инструментом ученика на уроке математики. Использование этого инструмента является «предметом обучения» [15]. Ученики приобретают навык использования калькулятора для решения задач в каждой теме. Кроме научного калькулятора, в обучении используются электронные таблицы, система динамической геометрии и, при необходимости, система компьютерной алгебры.
3. Геометрия изучается как отдельный учебный курс. Изучение геометрии начинается достаточно поздно (с 7 класса), в частности, стереометрия изучается в старшей школе на отведенном для этого учебном курсе. Пропедевтика изучения знаний из стереометрии осуществляется в 5–6 классах в разделе «Наглядная геометрия».	3. Начиная с младших классов, школьники знакомятся с геометрическими фигурами на плоскости, а впоследствии и в пространстве. В основной школе начинается изучение стереометрии. На экзаменах встречается большое количество стереометрических задач, описывающих реальные проблемные ситуации.
4. По программе проценты начинают изучаться в 6-м классе. Изучение начинается с основных понятий, таких как «процентное отношение», «нахождение процентов от числа», решение задач на проценты. Более сложные темы, такие как сложные проценты, обычно изучаются в 9 классе. Темы, связанные с процентами, изучаются обособленно от других элементов содержания, поэтому при отсутствии регулярного повторения зачастую забываются обучающимися.	4. Изучение процентов начинается в 5–6 классах (зависит от Федеральной земли), представлено во всех разделах математики, например, при изучении координатной прямой. При решении задач на снижение (повышение) стоимости товара может применяться схема изменения процентов на координатной прямой.
5. В 7–9 классах изучают различные виды функций, в том числе демонстрируются модели реальных ситуаций с помощью графиков, диаграмм. Показательную функцию не изучают в основной школе.	5. Особое внимание уделяется показательной функции и необходимости ее изучения для описания экспоненциальной зависимости величин из реальной жизни (на органический рост).
6. Элементы комбинаторики представлены в начальной школе. Вероятность и статистика с 2023 года изучается во всех 7–9-х классах.	6. Вероятность и комбинаторика изучаются с начальной школы. Особое внимание уделяется наглядности моделей в задачах.

Исследование прикладной направленности обучения математике в России и Германии актуально, так как использование прикладных задач в обучении математике позволяет учителю мотивировать учеников, показать применение математики, стимулировать исследовательскую деятельность обучающихся, укрепить межпредметные связи и сформировать практические навыки решения повседневных задач.

Анализ учебной и научной литературы [2; 4; 5; 16] позволяет сделать вывод о том, что изучение математики в Германии ориентировано на ее применение в реальных жизненных ситуациях, поэтому большое внимание уделяется ее прикладному значению, использованию цифровых математических инструментов. Сюжетные задачи формулируются на языке реальных ситуаций. В целом, немецкое математическое образование более прагматично и мобильно, в то время как российское – более фундаментально [4, с. 58]. В России большее внимание уделяется строгости математической теории, отработке применения алгоритмов и правил, изучению свойств математических объектов, решению математических задач.

Сравнивая федеральные образовательные стандарты России (ФГОС ООО [9]) и Германии (Bildungsstandart, Fachanforderungen [13; 17]), программы, кодификаторы и демонстрационные варианты экзаменов ОГЭ и BBR-9, MSA-10, можно выделить некоторые особенности содержания обучения математике школьников 12–15 лет в России и Германии (таб. на стр. 81).

Описанные отличительные особенности содержания обучения математике в России и Германии позволяют сделать вывод о том, что прикладные задачи, предлагающиеся немецким школьникам 12–15 лет, могут быть более разнообразными по используемым в решении математическим моделям.

В Германии сложность прикладных задач гораздо выше, они имеют более объемное условие, в них часто фигурируют реальные объекты, хорошо знакомые немецким школьникам (названия объектов архитектуры, природных объектов, реальные карты местности).

В России чаще в учебниках и на уроках используются псевдоприкладные задачи, демонстрирующие применение изучаемого теоретического материала на примере некоторой ситуации, которая описывается с использованием реальных объектов (машин, бригад, карт местности). Получение ответа в таких задачах обычно не имеет практической значимости в реальной жизни, но важно для закрепления изучаемого материала. В процессе обучения обязательно рассматриваются с учащимися задачи, аналогичные всем типам прикладных задач ОГЭ по математике. Обычно такие задачи, если и могут иметь различные способы решения, то всегда приводят к однозначному точному ответу.

Кроме фиксации наличия прикладных задач на уроках математики в немецких школах и описания особенностей таких задач, следует рассмотреть и методическое обеспечение обучения решению таких задач [16], элементы которого мы могли наблюдать на уроках в школах земель Саксония, Баден-Вюртемберг и Бавария в 2013 году во время специально организованного Московским институтом открытого образования сравнительного исследования качества математического образования России и Германии.

В немецких школах прикладные задачи вводятся через описание реальной ситуации. Поясняется значимость решения задачи для реальной жизни. Поощряется дивергентное мышление обучающихся. На уроках математики учитель поддерживает непринужденную атмосферу, укрепляет уверенность обучающихся в себе, проявляет интерес к неправильным идеям решения, конструктивно относится к ошибкам учащихся, стимулирует интуитивные рассуждения и догадки. Учителя используют эвристику (например, «решите более простую аналогичную задачу, «найдите необходимые и достаточные условия», «используйте компьютер», «структурируйте данные», «обобщите» и т.п.) и побуждают к самоконтролю.

В процессе обучения выделяется достаточный объем времени для решения прикладных задач, уделяется внимание всем этапам работы с задачей. Иногда решению одной или нескольких родственных прикладных задач может быть посвящен целый урок или несколько уроков.

Немецкие методисты отмечают затруднения обучающихся в решении нестандартных прикладных задач, к которым нелегко подобрать подходящий метод решения. Вследствие того, что ученики не могут определиться со стратегией работы с задачей, они чувствуют себя подавленными, что может отражаться на дисциплине [Там же, с. 1]. Среди возможных барьеров, не позволяющих обучающимся решить прикладную задачу, выделяются: объективный барьер (контекст задачи непонятен обучающимся) и субъективный барьер (обучающиеся не понимают, какое знание применить для решения задачи).

Важной особенностью процесса решения прикладных задач в Германии является использование округлений, приближенных вычислений. Например, ответ к задаче на вычисление всегда записывается в виде десятичной дроби. Данная особенность является следствием постоянного использования калькуляторов на уроках математики.

В 5–10 классах немецких школ Sekundarstufe 1 на уроках используются научные (инженерные) калькуляторы, обычно Casio (рис. 1) и цифровые математические инструменты (вычислительные и графические калькуляторы, программное обеспечение для изучения геометрии, электронные таблицы, программы для изучения стохастики). Каждая тема по математике изучается с применением калькуляторов, в том числе они используются при решении прикладных задач. В связи с этим ответ в прикладных задачах учащиеся записывают без использования символов радикалов и обыкновенных дробей, как это принято в России. Немецким школьникам разрешено использовать научный калькуляторы без графической поддержки во время экзаменов, в задания которых всегда включаются прикладные задачи.

Main

Statistics

MENU

ж

а

Conics

О О О О О О о о о о о о О О О О О ООООО ооооо о • © © ф

3D Graph ax=k

NumSolwe

Spreadsheet

Geometry

Sequence

Рис. 1. Калькуляторы, используемые учащимися в Германии

Покажем, как немецкие школьники используют калькулятор при решении задачи.

Задача №1. Уклон дороги обычно задается в процентах. Значение 12% на дорожном знаке означает, что каждые 100 метров высота дороги увеличивается на 12 метров. Определите угол наклона дороги (рис. 2).

Die Steigung einer StraBe wild in der Regel in Prozent angegeben.

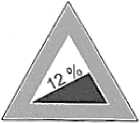
Die Angabe 12 % (= ^) auf dem abgebilde-ten Vcrkehrsschild bedeutet, dass pro 100 m in waagerechter Richtung die Hohe der StraBe um 12 m zunimmt.

Bestimme den Steigungswinkel der StraBe.

Рис. 2. Оригинал задачи №1 [20, с. 78]

Решение . Тангенс угла наклона дороги будет равен 0,12.

Считая, что ɑ – искомый угол, можем найти tgɑ = 0,12. С помощью калькулятора находим градусную меру угла: ɑ≈6,84°.

Ответ : 6,84°.

Развитие информационных технологий в XXI веке способствовало созданию и применению не только средств информатизации на уроках математики, но и электронных образовательных ресурсов. Одним из видов данного типа ресурсов являются он-лайн-графические калькуляторы (например, Desmos и GeoGebra), применение которых также распространено как в России, так и в Германии. Немецкие школьники часто используют их при решении геометрических задач и задач функциональной линии. Рассмотрим применение графического калькулятора Desmos при решении задачи.

Задача №2 . На поверхности пола в экспериментальной лаборатории обнаружена бактериальная среда, занимающая площадь, равную 1,6 см². В благоприятных условиях каждая бактерия делится на две бактерии каждую минуту. С увеличением численности бактерий увеличивается занимаемая ими площадь, причем в равное количество раз. Отразите рост бактериальной среды в первые 6 минут в таблице значений и на графике (рис. 3).

Eine Bakterienkultur belegt im Versuchslabor eine Flache von 1,6 cm2. Unter giinstigen Bedingungen verdoppelt sie sich jede Minute. Stelle das Wachstum der ersten 6 Minuten in einer Wertetabelle und als Graph dar.

Рис. 3. Оригинал задачи №2 [20, с. 128]

Особенность данной задачи в том, что требуется представить информацию в графической форме с помощью математических средств, а не просто получить числовой ответ.

Преимущество графического калькулятора в задаче №2 заключается в том, что обучающиеся по самостоятельно составленной аналитической схемы быстро получают наглядное представление модели реальной ситуации (рис. 4). Такая форма представления информации позволяет проще провести анализ модели реальной ситуации, сформулировать и решить дополнительные задачи.

Таким образом, электронные образовательные ресурсы и цифровые инструменты позволяют визуализировать математическую модель реальной ситуации, манипулировать изучаемыми объектами благодаря интерактивности, перенести внимание со сложных вычислений, приводимых к ответу, на разрешимость проблемы с помощью математических средств. Этим объясняется ежедневное использование калькуляторов на уроках математики в Германии.

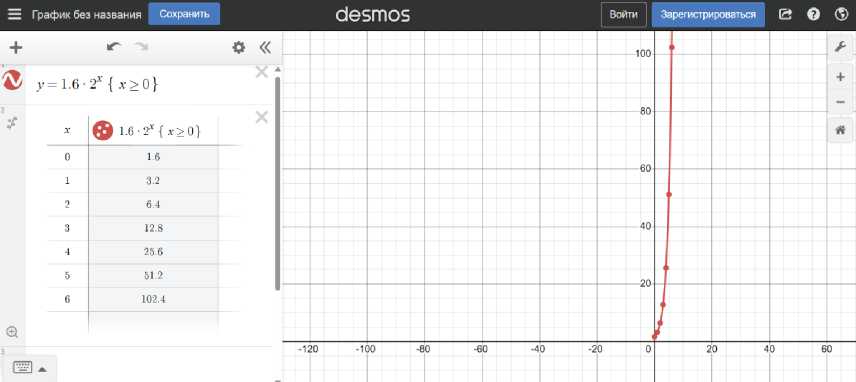
Рис. 4. Решение задачи №2 с помощью Desmos [14]

Сравним количество прикладных задач в российских и немецких учебниках по теме «Решение треугольников», имеющей обширный прикладной потенциал.

В учебнике Л.С. Атанасяна и др. в главе «Соотношения между сторонами и углами треугольника» [6, с. 271–293] содержатся 5 прикладных задач, что составляет 7,2% от всех задач главы, относящихся к рассматриваемой теме. В теоретической части главы описывается применение тригонометрии для двух практических ситуаций: измерения высоты предмета и определения расстояния до недоступной точки.

Рассмотрим на примере учебника Mathe.delta для земли Гессен особенности отражения прикладной направленности обучения математике в немецких школах. Следует отметить, что изложение теоретического материала включает описание и анализ ситуаций, которые встречаются в практической жизни или науке. При рассмотрении таких ситуаций ставятся цели изучения нового материала. Так, например, глава «Тригонометрия. Вычисление треугольников» [18, с. 7–38] начинается с описания измерений геодезистов XVI века с использованием тригонометрии и упоминания о применении тригонометрии астрономами. Учащиеся учатся определять уклон дороги, отраженный на предупреждающих знаках «Крутой спуск» и «Крутой подъем». Далее приводятся примеры использования тригонометрии для нахождения уклонов дорог: «…на Тур де Франс велосипедисты преодолевают подъемы до 18%, внедорожник способен подниматься примерно на 25°, лыжные трассы с черной маркировкой имеют уклон до 30°» [Там же, с. 8]. Данные примеры понятны учащимся, т.к. они встречаются им в реальной жизни. После изучения теоретического материала рассмотренные практические ситуации встретятся учащимся в задачах, например, в задаче №3, оригинал которой представлен на рисунке 5 (рис. 5 на стр. 86).

Задача №3. Для каждого случая определите величину угла наклона как на графике, так и с помощью своего калькулятора:

• а)    Перевал Сен-Готард-Пассштрассе 10%;

• б)    Цугшпиц-железная дорога 25%;

• в)    Автомагистраль 3%;

• г)    Перевал Яуфен 12%.

Ermittle jeweils die GrdBe des Steigungswinkels sowohl zeichnerisch, als auch mithilfe deines Taschenrechners.

• a) St.-Gotthard-PassstraBe 10 % b) Zugspitz-Zahnradbahn 25 %

• c) Autobahn3 %                  d) Jaufenpass 12 %

Рис. 5. Оригинал задачи №3 в учебнике [18, с. 9]

Отдельный параграф «Синус, косинус и тангенс в повседневной жизни» в учебнике [Там же, с. 14–15] включает только прикладные задачи, всего 14 штук.

Параграф «Геодезия и определение местоположения» содержит описание трех практических ситуаций, которые предлагается исследовать учащимся с применением тригонометрии и специальных инструментов для измерений (угломер-квадрант, приложения для смартфона). Описывается способ изготовления и применения отдельных инструментов, предлагается их использовать в практических измерениях на берегу реки или в школе. Для изучения каждой практической ситуации даются от трех до пяти прикладных заданий, сводящихся к применению тригонометрии на практике и анализу полученных математических моделей, а также к практическим измерениям.

В учебнике предложены проекты для учащихся, связанные с проведением собственных измерений с реальными измерительными инструментами:

• •    измерение высоты башни, деревьев или домов рядом со школой;

• •    нахождение угла падения солнечных лучей на землю;

• •    измерение расстояния между недоступными точками.

Всего в главу «Тригонометрия. Вычисление треугольников» включены описания проектов и трех прикладных ситуаций (11 заданий), а также 41 прикладная задача, что составляет 33% от всех задач главы.

Включение разнообразных прикладных задач в процесс обучения математике, рассмотрение прикладных ситуаций и организация проектов для школьников отличает школьное математическое образование в Германии от других стран. Одна из причин этого заключается в получившем широкое распространение немецком образовании STEM-подходе – специализированном междисциплинарном подходе в образовании, ориентированном на науку, технологии, инженерию и математику, а также на решение реальных практических задач. В России проводятся исследования в этом направлении [3; 8], однако широкого распространения в образовании они пока не получили.

В России и Германии различны Федеральные государственные образовательные стандарты, требования к выпускникам основной школы в области математической подготовки, условия среды и традиции. Тем не менее необходимость усиления прикладной направленности обучения математике наблюдается в обеих странах.

Повышение образовательных результатов школьников Германии, зафиксированное по результатам исследования PISA в 2015 году, было связано во многом с тем, что за первые пятнадцать лет XXI века учителя математики стали активно использовать в своем преподавании прикладные задачи, причем как составленные самостоятельно, так и представленные в немецких учебниках. Возросла роль таких задач в обучении математике, увеличилось их количество в учебниках и на уроках, сюжеты прикладных задач стали разнообразнее и доступнее учащимся. Использование цифровых инструментов позволило иначе расставить акценты при решении задач, перенеся внимание на применимость математических средств при решении проблем. Таким образом, были использованы различные организационные и методические приемы, средства и решения для целенаправленного усиления прикладной направленности обучения математике в школах Германии.

Расширение спектра прикладных задач, отражение в них реальных ситуаций, доступных для учащихся, систематическое включение таких задач в учебный процесс, использование электронных образовательных ресурсов и цифровых инструментов в процессе обучения математике при сохранении фундаментальности российского математического образования может повысить его качество и уровень вовлеченности учащихся в процесс обучения математике.