Дифракционная оптика, оптические технологии. Рубрика в журнале - Компьютерная оптика

Стоячие волны в невзаимных гиротропных средах
Статья научная
Рассмотрены особенности интерференции невзаимных прямых и обратных волн в продольно намагниченном ферримагнетике. Показано, что невзаимность параметров структур существенно влияет на характер резонансного процесса, в частности, приводит к отсутствию синфазности колебаний в разнесённых точках пространства, расположенных между узлами.
Бесплатно

Структура нормальных мод в параллельных идеальных оптических волокнах с сильной связью
Статья научная
В данной работе исследовано влияние сильной эванесцентной связи на структуру нормальных мод системы параллельных идеальных многомодовых оптических волокон. С использованием формализма теории возмущений с вырождением на основе скалярного волноводного уравнения для этой системы получены аналитические выражения супермод высших порядков и определены их постоянные распространения. Показано, что структура мод в случае сильной эванесцентной связи совпадает с аналогичной структурой нормальных мод для слабо связанных параллельных волокон. Продемонстрировано, что наличие сильной связи приводит к модификации выражений для поляризационных поправок к скалярной постоянной распространения, для которых получены соответствующие аналитические выражения.
Бесплатно

Структурная устойчивость спиральных пучков и тонкая структура потока энергии
Статья научная
Проблема структурной устойчивости волновых систем с многими степенями свободы непосредственно касается вопроса перераспределения потоков энергии в структурированных вихревых пучках, обеспечивающих их устойчивость при распространении и фокусировке. Особое место в этом многообразии занимают спиральные вихревые пучки, способные отображать сложные фигуры, буквы и даже слова. Спиральные пучки содержат бесконечное множество пучков Лагерра-Гаусса со строгой последовательностью топологических зарядов и радиальных чисел, их амплитуды и фазы жестко согласованы. Используя сочетание теории и компьютерного моделирования, подкрепленное экспериментом, мы проанализировали структуру критических точек в потоках энергии для двух основных типов спиральных пучков: треугольные пучки с нулевым радиальным числом и треугольные пучки со сложным обрамлением их граней и с обоими квантовыми числами. Структурная устойчивость обеспечивается триадами критических точек, как внутри, так и во внешней области треугольника, которые направляют световой поток вдоль треугольной образующей и удерживают обрамление при вращении пучка. Эксперимент показал, что простой треугольный спиральный пучок оказывается устойчивым даже при небольших неточностях юстировки, тогда как сложный треугольный пучок с обрамлением требует тщательной юстировки.
Бесплатно

Структурно-устойчивые трёхмерные и двумерные лазерные половинные пучки Пирси
Статья научная
Получено новое решение параксиального уравнения Гельмгольца, описывающее семейство структурно-устойчивых трёхмерных и двумерных половинных пучков Пирси (ПП-пучки). ПП-пучки обобщают пучки Пирси, полученные в Opt. Express, 20, 18955 (2012), так как известные пучки Пирси равны сумме двух ПП-пучков первого порядка. Угловой спектр плоских волн трёхмерных ПП-пучков отличен от нуля на половине параболы. Установлены свойства ортогональности функций, описывающих комплексные амплитуды ПП-пучков. Для двумерного ПП-пучка показано наличие ускорения в области до фокальной плоскости и замедление за фокусом.
Бесплатно

Структурные и оптические характеристики тонких пленок CdTe в видимом и инфракрасном диапазонах
Статья научная
Проведено исследование характеристик тонких плёнок CdTe, сформированных методом термовакуумного испарения из гранул CdTe на нагретые подложки. Структурные свойства CdTe были изучены с помощью растровой электронной микроскопии, рамановской спектроскопии. Исследование оптических свойств проводилось методом эллипсометрии, фурье-спектроскопии. Выявлены области низкого поглощения изготовленных плёнок в инфракрасном диапазоне. Для проверки возможности применения плёнок в сенсорике было проведено исследование структур металл/диэлектрик/диэлектрик на основе волноводного слоя CdTe для сред на основе воды, этанола и изопропанола, заключенных между плёнками CdTe и золота. В спектрах отражения этих структур наблюдаются резонансы в диапазонах длин волн, соответствующих локальным максимумам поглощения материалов. Выявлена зависимость положения резонансов в спектрах отражения от значений коэффициента поглощения растворителей. Полученные результаты могут быть использованы для разработки устройств фотоники инфракрасного диапазона.
Бесплатно

Субволновая локализация света в волноводных структурах
Статья научная
Моделирование с помощью программ FullWAVE и Fimmwave показало, что в градиентных планарных кремниевых секансных волноводах фундаментальная TE-мода может иметь ширину 0,09"lambda", "lambda" - длина волны; гибридная HE11 мода в полом кварцевом круглом ступенчатом волокне может иметь диаметр 0,03"lambda"; фундаментальная TM-мода в нанощели в кремниевом планарном волноводе имеет ширину 0,065"lambda"; планарная секансная градиентная микролинза разрешает два источника на расстоянии 0,15"lambda"; градиентная планарная линза "рыбий глаз" в зеркальном резонаторе изображает точечный источник в пятно шириной 0,18"lambda"; планарная секансная градиентная микролинза 6,5x5,34 мкм, использованная в качестве кольцевого резонатора, связывает два планарных субволновых волновода шириной 386 нм с эффективностью 79% (аналогичный кольцевой кремниевый резонатор имеет эффективность - 71%); в планарном металлическом волноводе световая мода (плазмон) распространяется вдоль краев волновода, проникая в сам волновод на величину 0,039"lambda" для серебра; в нанощели в серебряной пленке распространяется TM-мода (плазмон), полностью заполняющая эту щель шириной 50 нм (ширина моды 0,111"lambda").
Бесплатно

Субволновая фокусировка лазерного излучения с помощью зонной пластинки из хрома
Статья научная
Проведено исследование характеристик фокусного пятна, формируемого зонной пластинкой диаметром 15 мкм из пленки хрома на стеклянной подложке и фокусным расстоянием в одну длину волны λ = 532 нм, в зависимости от высоты рельефа. Исследование показало, что высота рельефа 70 нм позволяет достичь оптимального соотношения размеров фокусного пятна по полуспаду интенсивности и максимальной интенсивности. С использованием сканирующего ближнепольного оптического микроскопа показано, что зонная пластинка с указанными параметрами фокусирует линейно поляризованный Гауссов пучок в эллиптическое пятно с размерами по полуспаду интенсивности вдоль декартовых координат FWHMx = 0,42λ и FWHMy = 0,64λ.
Бесплатно

Субволновая фокусировка лазерного излучения смешанной азимутально-линейной поляризации
Статья научная
В данной работе был рассмотрен четырёхсекторный пропускающий преобразователь поляризации для длины волны 633 нм, с помощью которого можно получить азимутально-поляризованный пучок из линейно-поляризованного. Численно показано, что, поместив непосредственно за преобразователем поляризации зонную пластинку Френеля с фокусным расстоянием 532 нм, можно сфокусировать свет в субволновое фокусное пятно с размерами по полуспаду интенсивности меньше дифракционного предела (размеры по полуспаду интенсивности равны 0,28 и 0,45 от длины волны фокусируемого света). Если же после прохождения четырёхсекторного пропускающего преобразователя свет сначала распространяется в свободном пространстве на расстояние 300 мкм и только потом фокусируется зонной пластинкой, то размер фокусного пятна составляет 0,42 и 0,81 от длины волны фокусируемого света (при этом размер пятна, сформированного только поперечной составляющей напряженности электрического поля, был равен 0,42 и 0,59 от длины волны). Последний численный результат был проверен экспериментально, полученные размеры пятна были равны 0,46 и 0,57 от длины волны.
Бесплатно

Субволновая фокусировка с помощью бинарного микроаксикона с периодом 800 нм
Статья научная
С помощью сканирующего микроскопа ближнего поля NT-MDT c кантиливером с отверстием 100 нм на расстоянии 100 нм от поверхности микроаксикона с диаметром 13,6 мкм периодом 800 нм и глубиной 465 нм, изготовленного совместно ИСОИ РАН и Университетом Сэнт-Эндрюса (Шотландия) по технологии электронной литографии на резисте ZEP520A, измерено фокусное пятно линейно-поляризованного лазерного света с длиной волны 532 нм, которое имело диаметр по полуспаду интенсивности равный 320 нм, что составляет 0,61 от длины волны. Глубина фокусировки по полуспаду интенсивности была равна 3 мкм, причём экспериментальные точки осевой интенсивности в фокусном отрезке с хорошей точностью (с.к.о. 13%) наложились на расчётную кривую осевой интенсивности, а приближённая оценка и строгое моделирование дают диаметр фокусного пятна по полуспаду интенсивности равный 0,54 от длины волны. Интенсивность в максимуме на оптической оси в 7 раз больше, чем интенсивность освещающего пучка.
Бесплатно
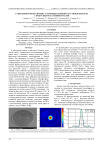
Субволновая фокусировка с помощью зонной пластинки Френеля с фокусным расстоянием 532 нм
Статья научная
Изготовлена и исследована фазовая бинарная зонная пластинка с фокусным расстоянием 532 нм, радиусом 7,7 мкм и глубиной рельефа 510 нм. С помощью ближнепольного микроскопа показано, что при освещении пластинки линейно поляризованным Гауссовым пучком с длиной волны 532 нм формируется фокусное пятно с диаметром интенсивности по полуспаду, равным 0,44 от длины волны.
Бесплатно

Суперпозиция вихревых световых пучков для захвата и перемещения биологических микрообъектов
Статья научная
В статье рассматривается возможность формирования модифицированной оптической ловушки для биологических микрообъектов из суперпозиции вихревых световых пучков. Представлены результаты экспериментов с использованием таких пучков.
Бесплатно

Суперпозиция двух смещенных с оптической оси пучков Лагерра-Гаусса
Статья научная
В работе найдены топологические заряды суперпозиции двух симметрично-смещенных с оптической оси пучков Лагерра-Гаусса с номерами (0, m ) и (0, n ). Показано, что если m = n , тотопологический заряд суперпозиции равен n . То есть два одинаковых смещенных с оптической оси пучка Лагерра-Гаусса имеют топологический заряд, как один пучок Лагерра-Гаусса. Если m 1 = ( m + n ) / 2, TC2 = TC1 + 1, TC3 = TC1 + 1/2 и TC4 = TC1 - 1/2. Правила выбора одного из 4 значений топологических зарядов также установлены. При отсутствии смещения с оптической оси двух пучков Лагерра-Гауссатопологический заряд суперпозиции равен большему из двух топологических зарядов, то есть n . А при любом сколь угодно малом смещении с оптической оси топологический заряд суперпозиции либо остается таким же, как до смещения, либо уменьшается на четное число. Это объясняется тем, что из бесконечности «приходит» четное число оптических вихрей с топологическим зарядом- 1, которые компенсируют такое же число оптических вихрей в суперпозиции с топологическим зарядом + 1. Интересно также, что при сложении двух смещенных с оптической оси пучков Лагерра-Гаусса с определенными наклонами к оптической оси, такими, чтобы суперпозиция являлась структурно-устойчивым пучком, на некоторой линии формируется бесконечное число винтовых дислокаций с топологическим зарядом + 1. Полный топологический заряд такой суперпозиции бесконечный.
Бесплатно

Суперструктурированные адресные волоконные брэгговские структуры
Статья научная
Представлены результаты теоретического исследования возможностей многоадресных волоконно-оптических брэгговских структур, сформированных на базе комбинации массива из однородных слабоотражающих волоконных решеток Брэгга и специально структурированных дискретных фазовых сдвигов. Исследование проведено на основе математического аппарата матриц рассеяния и передачи. Полученные решения открывают новые перспективы для интеграции многоадресных волоконно-оптических брэгговских структур в устройства радиофотоники и волоконно-оптические сенсорные системы, обеспечивая формирование нового класса как радиофотонных устройств, так и базовых пассивных оптических элементов. Рассмотренные в работе многоадресные брэгговские структуры одновременно выполняют роль как формирователей радиофотонного излучения, так и чувствительных элементов, что обеспечивает выполнение ключевых требований, предъявляемых к компонентам радиофотонных систем в целом. Приведены принципы управления спектральными характеристиками многоадресных систем данного класса.
Бесплатно

Теоремы о сохранении орбитального углового момента суперпозиций смещённых оптических вихрей
Статья научная
Доказаны две теоремы о сохранении орбитального углового момента (ОУМ) суперпозиции одинаковых оптических вихрей с произвольной радиально-симметричной формой и целым топологическим зарядом n, смещённых с оптической оси. Нормированный ОУМ такой суперпозиции при произвольном смещении центров пучков с оптической оси и при любых вещественных весовых коэффициентах равен ОУМ каждого отдельного пучка, входящего в суперпозицию. Если центры пучков находятся на одной прямой, проходящей через начало координат, то даже при комплексных весовых коэффициентах нормированный ОУМ суперпозиции равен ОУМ каждого отдельного входящего в неё пучка. Эти теоремы позволяют формировать лазерные вихревые пучки с разным (не обязательно радиально-симметричным) распределением интенсивности, но обладающие одинаковым ОУМ. Приведены результаты численного моделирования для суперпозиций пучков Бесселя, Ханкеля-Бесселя, Бесселя-Гаусса и Лагерра-Гаусса с одинаковыми ОУМ.
Бесплатно

Статья научная
Проведено аналитическое и численное исследование формирования цилиндрических векторных пучков в двулучепреломляющих кристаллах по схемам с одним совмещённым фокусом и с двумя фокусами. В схеме с двумя фокусами при наличии вихревой фазы у исходного пучка c круговой поляризацией в одном из фокусов формируется радиально-поляризованное распределение, а в другом - азимутально-поляризованное. Данные результаты обобщены на случай формирования радиально- и азимутально-поляризованных лазерных мод высших порядков. Натурные эксперименты с кристаллом исландского шпата подтверждают результаты моделирования.
Бесплатно

Теория возмущений для уравнения Шрёдингера в периодической среде в квазиимпульсном представлении
Статья научная
В статье проанализированы некоторые известные результаты о движении осциллятора Блоха в кристалле в импульсном представлении. Показано, что описание движения электрона в изложении ряда авторов является неполным. На самом деле, точное описание поведения электрона в кристаллической решётке возможно только на основе решения уравнения Шрёдингера в импульсном представлении. В работе получены приближённые решения уравнения Шрёдингера для электрона в периодическом потенциале кристаллической решётки и уравнения для эволюции средних значений оператора импульса и координаты. Для описания поведения электрона в кристаллической решётке при наличии однородного электрического поля и возмущения, вызванного внешней электромагнитной волной, использована теория возмущений. Представленные методы в дальнейшем можно использовать для расчёта оптических устройств, в том числе оптических транзисторов.
Бесплатно

Теория катастроф и каустики радиально-симметричных пучков
Статья научная
Работа посвящена исследованию каустик радиальных пучков. Найдены аналитические выражения для каустических поверхностей волновых фронтов, создаваемых радиально-симметричными дифракционными оптическими элементами. Результат представлен в криволинейной системе координат, согласованной с каустической поверхностью. Получено асимптотическое представление интеграла Кирхгофа вблизи оптической оси, обеспечивающее корректность расчетов в непараксиальном случае.
Бесплатно

Теория связанных мод для резонансных дифракционных решёток с изменяющимся периодом
Статья научная
В работе предложена теория связанных мод для резонансных дифракционных решеток с изменяющимся периодом. Рассмотрены дифракционные структуры, у которых вектор обратной решетки - величина, обратно пропорциональная периоду, - линейно изменяется в направлении периодичности. Показано, что оптические свойства такой структуры существенным образом зависят от скорости изменения периода. На основе сравнения с результатами строгого численного моделирования в рамках метода фурье-мод показана высокая точность предложенной теоретической модели. В частности, разработанная теория связанных мод описывает уширение резонансного пика и появление вторичных максимумов, вызванные ненулевой скоростью изменения периода. Полученные результаты могут найти применение при разработке линейно изменяющихся спектральных фильтров на основе резонансных дифракционных решеток с изменяющимися параметрами.
Бесплатно

Статья научная
Проведены сравнительные исследования характеристик Бесселевых и «совершенных» пучков с топологическим зарядом 9, созданных с помощью бинарного кремниевого аксикона и «голографического» алмазного аксикона с непрерывным профилем при значении длины волны 141 мкм на Новосибирском лазере на свободных электронах. Сформированы пучки с линейной, азимутальной и радиальной поляризацией. Проведено сравнение поперечного сечения пучков, созданных разными аксиконами, в зависимости от расстояния. Приведен пример применения совершенных пучков с радиальной поляризацией для возбуждения вихревых плазмон-поляритонов на цилиндрическом проводнике.
Бесплатно

Термооптические аберрации радиально-симметричных дифракционных оптических элементов
Статья научная
Получены аналитические выражения температурного изменения аберрационных коэффициентов радиально-симметричного дифракционного оптического элемента в приближении третьего порядка малости, а также условие устранения терморасфокусировки дифракционно-рефракционного синглета. Проанализированы возможности коррекции аберраций в широком температурном диапазоне как одиночного дифракционного оптического элемента, так и дифракционно-рефракционного синглета.
Бесплатно

